Jacob Bernoulli

Miért a Shell Nautilus van ez a furcsa és elegáns megjelenés?

Az elején a tanulmány ezt a spirált kell csatlakoztatni a navigációt. A XVI és XVII században, több ezer hajó vitorlázott az óceánok. Mariners tudják, hogy a föld felszínén a legrövidebb távolság két pont között ad egy körív. De ahhoz, hogy ez a mozgás ív kell folyamatosan változás irányát. Ezért a legjobb, helyébe egy másik, oly módon, hogy az a szög, amelyet a hajó átkelés minden meridiánok, állandó volt. Ez az arány változatlan maradt. A pályái ilyen típusú vannak kialakítva a föld felszínén görbék úgynevezett loxodrome. Azonban a matrózok nem működött a területen, ezek a térképek lakás, ők egy vetülete a szférában. Nos, a vetítés egy gömb síkra alakítja loxodromes rajta ... logaritmikus (vagy konform) spirál.

Az első leírni, mint egy mechanikus görbe, ellentétben algebrai görbék volt Descartes, aki 1638-ban írta a szerzetes Mersenne a kutatásaik eredményeit. Descartes keresett növekvő görbéje hasonló tulajdonságokkal rendelkező egy körbe, úgy, hogy az érintő minden pontban által kialakított sugár vektor minden egyes pont mindig ugyanabban a szögben. Innen a neve konform. Azt is kimutatták, hogy ez a feltétel egyenértékű a poláros szögei pontok a görbe arányos a logaritmusai sugár vektorok. Ezért a második neve: a logaritmikus spirál. A távolság a tekercsek nő a növekvő szögben, azaz. E. A rádiuszvektorhoz exponenciálisan nő a növekvő forgási szög. Ahhoz, hogy a harmadik címet a görbe - geometriai spirál.

Atyja ezt a spirált, minden tisztességes, Jacob Bernoulli, hogy alaposan megvizsgálták, és ő annyira lenyűgözte, hogy megkérdezte, hogy ábrázolni vele sírját a temetőben Bázelben a felirat: „eadem mutata resurgo '(” Megváltozott, én még egyszer feltámad " „).
Kőfaragó nem volt jó matematikus. és ő faragott kő szinte tökéletes archimedesi spirál.

Jacob Bernoulli felfedezett néhány tulajdonságát ennek a görbének, amely észrevétlen maradt
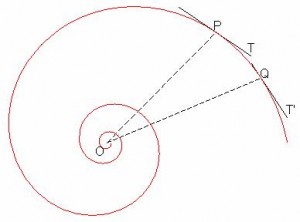
Descartes és Torricelli, beleértve azt a tényt, hogy a logaritmikus spirál - egyedülálló görbe, evolután, a bonyolult, maró hatású, és amelyek szintén verje meg, viszont logaritmikus spirál. Jacob Bernoulli felfedezett egy másik különlegessége,
önhasonlóság, amely közvetlenül összekapcsolja a spirál fraktálok.

A logaritmikus spirál kétségtelenül egy spirál, amely a leggyakrabban a természetben megtalálható. Animal Kingdom biztosít számunkra példát spirál csigák és kagyló. Mindezen formák arra utalnak, természeti jelenség: a kanyargós folyamat kapcsolódik a növekedési folyamatot. Tény, hogy a csigaház - ez nem más, se kevesebb, mint a kúp, feltekerve is. Horns kérődzők is, de ők is sodort. És bár a fizikai növekedés a jogszabályok eltérőek a különböző fajok, a matematikai törvények szabályozzák, hogy ezek ugyanazok: ezek valamennyien geometriai spirál önhasonló görbét. Ha jobban megnézzük a növekedés a héj és a szarvak, tudomásul vesszük, egy másik érdekes tulajdonsága: a növekedés akkor csak az egyik végén. És ez a tulajdonság megtartja alakját teljesen egyedülálló a görbék matematikai, logaritmikus vagy egyenlő szögű spirál.

1 Slobodyaniuk VK.:

A logaritmikus spirál bányászatban fordul elő.
Útvonal spirális alakzat egy logaritmikus spirál.
Egyes tankönyvek fejlesztése nyílt hiba van, amikor a pálya nem jelent logaritmikus spirál, egyfajta archimedesi spirál (pontosan úgy, ahogy a Bernoulli sírjára).
Adok egy linket egy cikket, melyben hatását vizsgálta az útvonal paraméterek a tőke bányászati ​​tevékenység alapján a térbeli tulajdonságok a logaritmikus spirál.

2 Elizabeth A. Kalinin:

Köszönöm, ez nagyon érdekes, és csodálatos!

4 Elizabeth A. Kalinin:

Maxim, köszönöm egy érdekes és hasznos kiegészítője!

Hagyjuk meg véleményét