Periódusai konvexitás és inflexiós pont
Ütemezése differenciálható konvex függvény hívódik meg (fel) intervallumon, ha az a fenti (lásd alább) bármely tangens függvény ebben az intervallumban.
a grafikon pont elválasztó különböző részein a konvexitás, úgynevezett inflexiós pontban.
Tétel: Ha a függvény minden pontján az intervallum negatív (pozitív), a második derivált, a grafikon a funkció ez az időköz konvex, felfelé irányuló (lefelé irányuló).
2. példa Annak meghatározására időközönként konvexitás és inflexiós pont a grafikon
Ahhoz, hogy megtalálja az intervallumok konvexitás és inflexiós pontot kell találni a második derivált függvények;
Egyenlővé a második derivált nullára, és megoldja a kapott egyenlet:
A kapott számszerű pont ossza szét két intervallum tengely. Annak megállapításához, a jel a második derivált ezen időtartamok :;
Mivel a pont tartozik a grafikonon, és amikor áthalad, akkor a második derivált előjelet, akkor - az inflexiós pont a grafikonon funkciókat.
Az intervallum, a második derivált negatív, ez azt jelenti, hogy a funkció grafikon felfelé domború. Ennek megfelelően, az intervallum funkció gráf konvex lefelé.
Ha x → + ∞, x → - ∞ vagy annak közelében a töréspontok a 2. típusú függvény grafikonját tetszőlegesen szorosan megközelíti egy egyenes vonal. Ezeket a sorokat nevezzük aszimptotákkal.
Ez a vonal az úgynevezett függőleges aszimptotájának a grafikont a funkció, ha legalább az egyik egyoldalú korlátai ezt a funkciót tochkea jelentése + ∞ vagy -∞.
Meg kell azonban jegyezni, hogy megtalálja a függőleges aszimptóta elég pontokat találni diszkontinuitás a 2. fajta. Ha ez a funkció egy töréspontot egy. majd - vertikális asymptote.
Ferde asymptote grafikus függvény az y = f (x) formájában van y = kx + b. ahol
.
Vegye figyelembe, hogy ha legalább az egyik együtthatók vagy b egyenlő a végtelenbe, arra lehet következtetni, hogy a lejtőn a asymptote ott.
Ha k = 0. a függőleges aszimptóta van írva a formában y = b. Ezt a vonalat nevezzük vízszintes asymptote.
Példa 3. Keresse meg a asymptote funkció
Nyilvánvaló, hogy a pont lesz a második fajta töréspontot, majd egyenesen a függőleges aszimptotáját a függvény grafikonját.
Megvizsgáljuk, hogy a funkció lesz hajlandó asymptote:
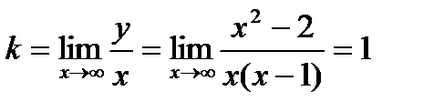
Ez azt jelenti, egyenes - ferde aszimptotája a grafikon funkciók.
Az általános rendszer a kutatási funkció
1.Nayti domén funkcióit.
2.Find a grafikont a metszéspontok a koordináta-tengely.
3.Nayti szélsőséges funkciókat.
4.Nayti monotonitás időközönként.
5.Nayti időközönként konvexitás és inflexiós pont.
7.Nayti értékrend
4. példa Annak vizsgálatára, a funkció és a konstrukció a grafikon
Mi meg fogja vizsgálni az általános rendszer funkció:
1. Nyilvánvaló, hogy. Ezért OOF:
2. Keresse meg a metszéspont a koordináta tengelyekkel:
. Kapott pont (-, 0); (, 0)
3. Adjuk meg a szélsőséges funkciók:
X = 1 - maximális pont (1; 2)
X = 3 - minimális pont (3; 6)
4. Az A reakcióvázlat a fent kapott arra a következtetésre jutunk, hogy a
ha a funkció növekszik;
ha a funkció csökken.
A második derivált feltételezi pozitív és negatív értékek a. Következésképpen, ha az ütemezés függvény konvex lefelé, és a grafikon a amikor egy dudor felfelé.
A lényeg a diagram osztja különböző convexity, de mivel ez nem tartozik a menetrend, az inflexiós pont nem. Egyéb pontok elválasztó része a grafikon nem más convexity. Tehát azt mondhatjuk, hogy nincs inflexiós pont.
6. tanulmányozza a funkciót a asymptote
Nyilvánvaló, hogy a vonal - egy függőleges aszimptotája a függvény grafikonját.
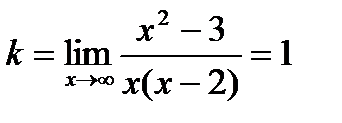
Ezek szerint pont úgy megépíteni a függvény grafikonját, valamint a aszimptotáját a grafikon.
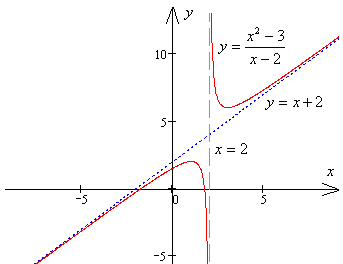
7. A grafikon azt mutatja, hogy a függvény összes értékét a valós tengelyen, mint az intervallum a maximális és minimális a funkció, azaz a beállított függvények értékét.
F (x) függvény az úgynevezett primitív függvény f (x) az időtartam, ha, minden x ebben az intervallumban, a egyenlőséget F „(x) = f (x). A készlet minden primitívek f (x): F (x) + C. GDE - állandó és az úgynevezett határozatlan integrál.
Az ingatlan a határozatlan integrál:
5) Ha. akkor. ahol - tetszőleges differenciálható függvény.