Ellenőrizze tartozik, hogy egy adott ponton a szegmens (határozza meg) körök - verem túlcsordulás
Hello. Kérem, segítsen. Az általános probléma: egy koordinátarendszerben megadott szegmenst kezdődő pontnál kezdődik, és a B pontot is állítsa körök (1 doboz kör) központokkal pontokon M1, M2, M3. M100 és a sugarakkal R1, R2, R3. R100. Meg kell ellenőrizni, hogy tartozik egy adott ponton az intervallumban (set) körökben.
Általában a program működik, de ez valószínűleg nem mindig helyes. Már próbáltam egy csomó teszt esetek, minden helyesen azonosítja. De amikor elküldi a döntés az olimpia, akkor a szerver azt mondja: „Rossz válasz”. Vétkezzem minden típusú. Te is segíthetsz?
Az ábra azt mutatja, két esetben a nem-kereszteződés köríven:
- Ha a vonal nem metszi a kört.
- Amikor a vonal metszi a kerülete, és a szegmens nem metszi.
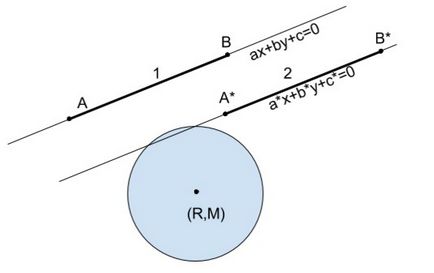
Minden egyes kör (R, M), és a szegmens AB lehetséges alkalmazni az alábbi algoritmus:
- Kiszámoltuk az együtthatók az egyenlet
(A + qB) / (1 + q) a (R, M). vagy
(Xa + q * XB - (1 + q) * xm) 2 + (ya + q * Yb - (1 + q) * ym) = 2 (1 + q) 2 * R 2:
2 C 2 q + 2C1 q + C0 = 0, ahol a
C0 = (xa - XM) 2 + (ya - ym) 2 - R 2,
C1 = (xa - XM) * (xb - XM) + (ya - ym) * (Yb - ym) - R 2,
C2 = (xb - XM) 2 + (yb - ym) 2 - R 2. - Ha C0 <= 0, точка A попала в круг.
- Ha C2 <= 0, точка B попала в круг.
- Ha 2 det = C1 - C0 C2 <= 0, прямая АB с кругом не пересекается.
- Kiszámoljuk a gyökerek Q1 és Q2 (ha van ilyen).
- Ha q1> = 0 vagy Q2> = 0. a találatot. Egyébként mi nem hit.