Al bázis egy egyenlő szárú háromszög 12, a geometria

AU bázis egy egyenlő szárú háromszög egyenlő 12

Szia barátok!
Ma megnézzük a problémát a tanfolyam 8. évfolyamon, ami szintén hasznos és aktuális diplomások
9. évfolyamon.
Azért, mert használják a képlet, hogy meghatározzák a
háromszög területén a sugarak a beírt és körülírt körök.

célkitűzés:
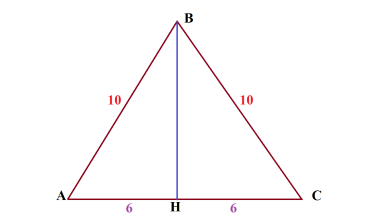
Az alap egy egyenlő szárú háromszög 12 cm. És oldalait egyenlő 10cm. Keresse meg a a sugara a háromszög köré írt kör a háromszög!

Megoldás: csepp merőleges a tetején BH
A háromszög alapja az AU.
Tudjuk, hogy a függőleges felezővonal és egyben a medián egy egyenlő szárú háromszög. Ie AH = CH = 6 cm.

AVN a derékszögű háromszög ismerve a átfogója AB = 10cm,
befogó és az AH = 6 cm, keresse meg a második befogó HV.
A tétel Püthagorász HV = √ (10² - 6²) = √64 = 8.
Ennélfogva, a terület a ABC háromszög lehet kiszámítani a következő képlettel
S = 1/2 * SS * BH = 1/2 * 12 * 8 = 48sm².

Azonban, a háromszög területe lehet kiszámítani a képletben az S = pr,
ahol p - semiperimeter háromszög, p = (10 + 10 + 12) / 2 = 16
r - a sugara a beírt kör.
Van: PR = 48 ⇒ r = 48 / p = 48/16 = 3 cm.

A háromszög területe révén a termék oldalán
és fejezhető a sugara a körülírt kör:
S = abc / 4R, ahol
a, b, c - oldalán a háromszög,
R - a kör sugara.

A háromszög területe ismerjük, az oldalak hosszát is
Találunk a sugár.
48 = 10 * 10 * 12 / 4R ⇒
R = 10 * 10 * 12/4 * 48 = 6,25sm.

A: a sugár beírható kör egyenlő 3 cm,
A kör sugara egyenlő 6,25 cm.

Mert ma. A siker és az új kihívásokra!

Azt is lehet, hogy érdekel:

• 
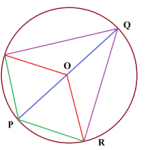
  Keresztül a P pont és a kör átmérője végzett két akkordok
• 
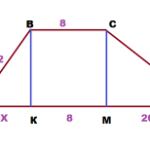
  A magasság a trapéz, és a 8 alapban 28
• 
  Példák 7 geometria osztályt.