A felület a Fermi
Alapozza Szilárdtestfizikai,
Akarta, hogy írásaiban több szórakoztató, ők [az írók] kezelik, hogy az olvasó a legdurvább találmányok ".
Jonathan Swift „Gulliver utazásai”
A Fermi-felület nem igazi arc és világosan mutatja a viselkedése elektronok fémek! Képek Fermi felületek megmagyarázni tulajdonságai fémek, mint a ragyogó, alakíthatóság, vezetőképesség és hővezetés. Tulajdonképpen a fém lehet meghatározni, mint egy szilárd anyag rendelkezik a Fermi felület.
Fizikailag Fermi felület úgy definiáljuk, mint a felületi energiája az elektronok állandó ε F impulzusa k-space.
Alapozza Szilárdtestfizikai,
Transzlációs szimmetria ró saját jellemzői a Fermi-felület, még abban az esetben, ha figyelembe vesszük a lehetséges ionok nullára. Tekintsünk egy kétdimenziós példát az érthetőség kedvéért.
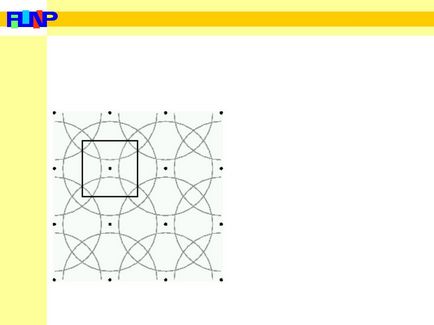
A fekete vonal mutatja az első három zónára Brillouin négyzetrács (rácspontok jelölt fekete pontok). Kék kör felel felületek állandó energiájú szabad elektronok
(Fermi felület két dimenzióban) egy bizonyos koncentráció.
Alapozza Szilárdtestfizikai,
Azonban ebben a rendszerben a kiterjesztett zónák Fermi felületi mintázat nem folytonos, és hiányzik belőle tisztaság
Most csinálj egy kétdimenziós Fermi felület közelében mindegyik reciprokrács. A fekete négyzet mutatja az első Brillouin övezetben. Minden pont a k prost- a tér, amely beleesik legalább egyik kör megegyezik a töltött elektron állapotok az első Brillouin övezetben. Pont alá egyszerre két kört találkozik zapolennnym államok a második Brillouin zónában, míg a három - a harmadik, stb
Alapozza Szilárdtestfizikai,
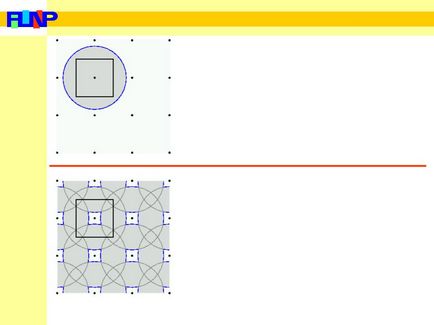
Így megkapjuk az alábbi képet. Fekete négyzet az ábrán - az első Brillouin övezetben. Kék kör - a Fermi-felület. Szürke terület - elfoglalt elektronikus államokban. Így a mi példánkban az első zóna teljesen fel van töltve.
Mi jár a második zónát. Fekete négyzet újra - az első Brillouin övezetben. Kék vonal - a Fermi felület a második Brillouin zónában. Szürke szín azt mutatja, a töltött elektron állapotok a második Brillouin zónában.

Alapozza Szilárdtestfizikai,
Most rátérünk az esetben, ha a lehetséges az ion mag nem nulla, de gyenge ahhoz, hogy használni perturbációszámítás. Az egydimenziós esetben láttuk, hogy a gyenge periodikus potenciált vezet elektron diffrakciós hatások mellett a határokat a Brillouin zóna és a megjelenése repedések a elektron energia spektrumot. Hasonlóképpen, van is ebben a két dimenziós eset.
Ahhoz, hogy minőségileg elképzelni, hogy a Fermi felület miatt módosult a gyenge kapacitása a kristályrács, meg kell emlékezni három szabály:
1. A Fermi-felület metszi a határ a Brillouin zóna merőleges a felületek
2. Fermi felület nem folyamatosan változtatható, amikor áthalad a határövezetben, mert ez azt jelentené, hogy a szomszédos területek közelében határain elektron energia változik. Azaz mentén tartományhatárokon léteznie kell ugrás értékét a hullám vektor az elektronok.
3. Ugyanezen értékek nagysága a hullám vektor az elektronok │energiya │ k az első zónában alatti energia az elektronok a második zónában, stb Ennek eredményeként, az elektronok áramlását a második zóna, hogy az első, de a
terület (térfogat háromdimenziós esetben) felületen Fermi tartani.
Alapozza Szilárdtestfizikai,
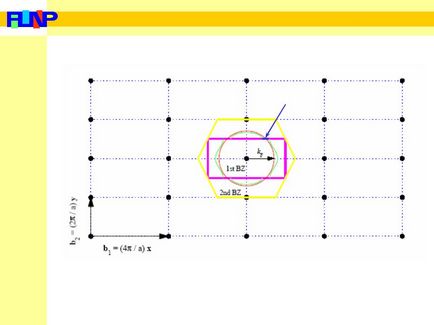
Szem előtt tartva a megjelölt szabályok, kap egy képet a deformálódhat a rács lehetséges a Fermi-felület.
Jump értékek wavevector
Ábra magenta és sárga szín azt mutatja, az első és a második Brillouin zóna téglalap reciprokrács. A piros kör - Fermi felület a szabad elektronok, és a zöld látható
Előadás №4 Fermi felület torz gyenge rács lehetséges.
Alapozza Szilárdtestfizikai,
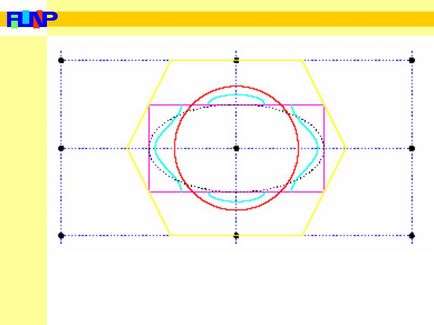
Így lesz a kép a rendszer a rendszeres zónákat. Balra - a Fermi felület az első Brillouin zónában, a jobb oldalon - a második. Szürke színű show tele elektronikus állapotban.
A növekedési potenciálját a rács azt eredményezi, hogy több elektront hajlamosak áramlást az első Brillouin zónában. Ennek eredményeként, a hangerőt a Fermi felület az első zónában növeli miatt a csökkentéséhez a második. Amikor egy kellően erős kristály potenciállal, minden elektronok lesz az első Brillouin zónában (szürke pontozott vonal az ábrán).