Az alkalmazás módja A konjugátum irányok Powell
A módszer középpontjában a problémák megoldására másodfokú célfüggvény és alapjául az alapvető elméleti eredményeket. Bár használt valós helyzetekben, az algoritmusok hatásosak másodfokú objektív funkciók nem működnek jól a bonyolultabb célfüggvény, ez a megközelítés azonban úgy tűnik, hogy teljesen ésszerű.
Definíció. enged


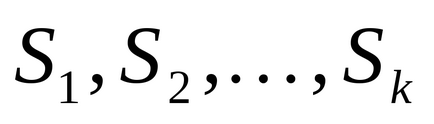


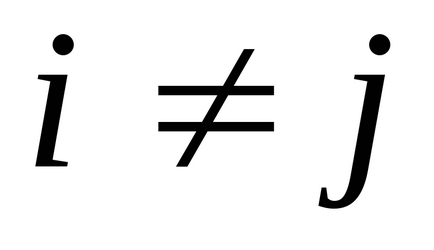
Példa. Tekintsük az
.
a sablon

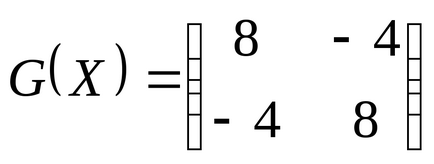
Mint az egyik irányba úgy döntünk
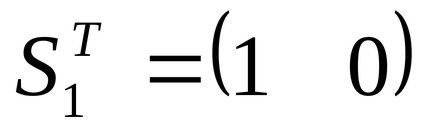
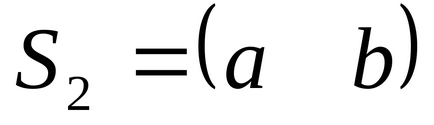
.
Meg kell jegyezni, hogy a konjugátum választott irányban egyértelmű. Azonban, ha hozzáadjuk a normalizációs feltételt, akkor lehet egyértelműen definiálva:
.
Jóváhagyása. Bármilyen másodfokú függvény
Egy tetszőleges függvény lehet kellőképpen képviselve a környezetében optimális pont a kvadratikus közelítéssel. Tehát a konjugátum irányba hasznos lehet annak optimalizálás. De ez több, mint
Jóváhagyása. Adott egy másodfokú függvény
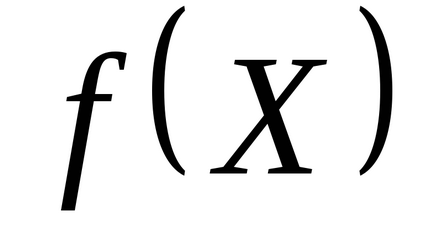
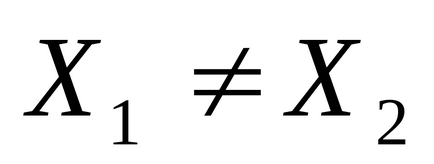
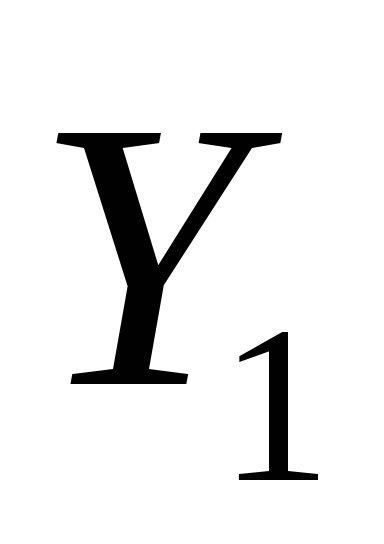
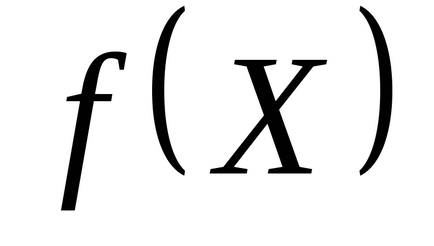
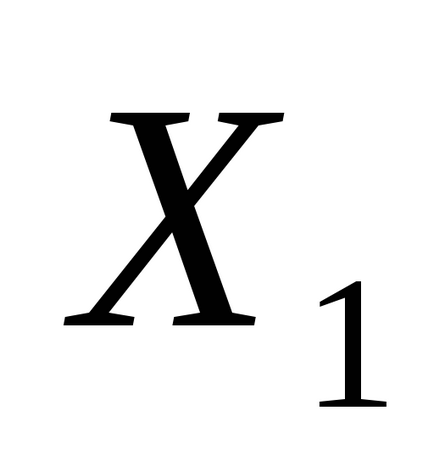
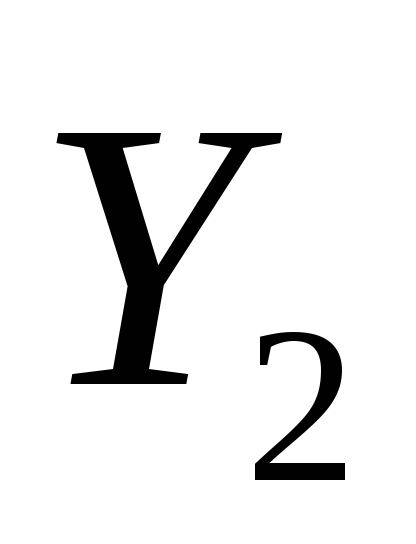
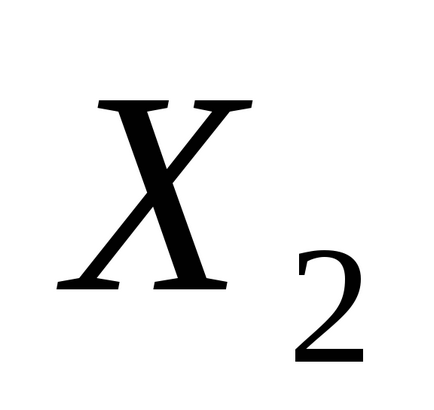
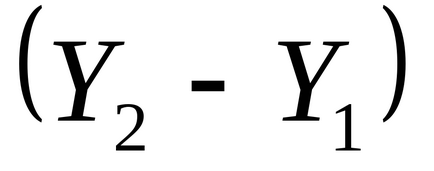
1. lépés: a kiindulási pont
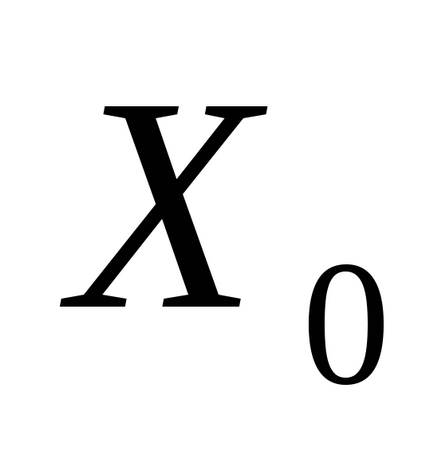
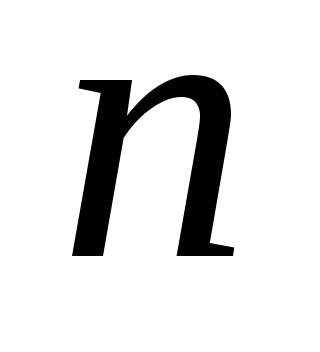

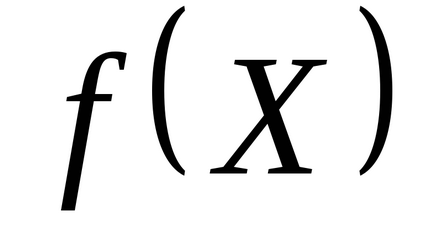
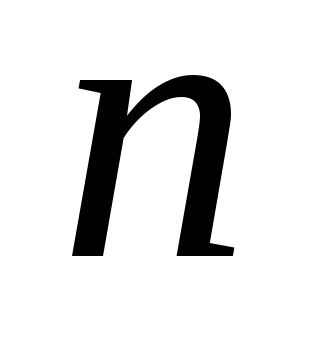
2. lépés: Futtassa az extra lépés
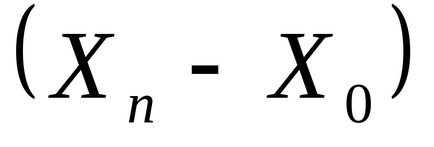
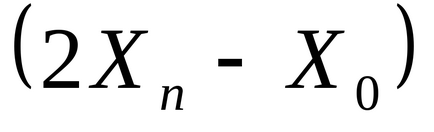
3. lépés: Legyen


és
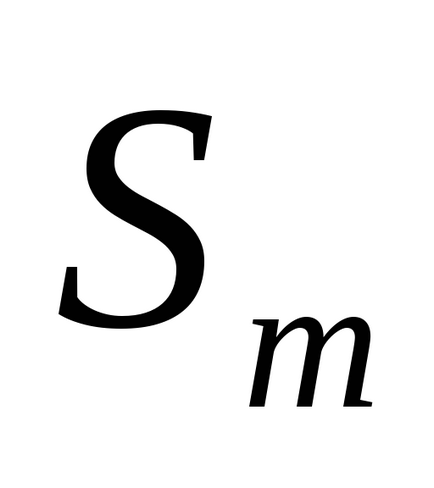

Ha a feltételek
(*)
A keresés folytatásához mentén az eredeti irányban

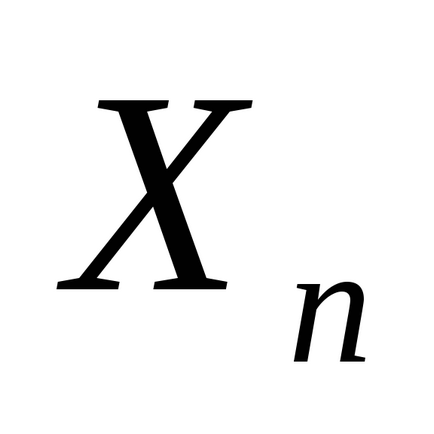
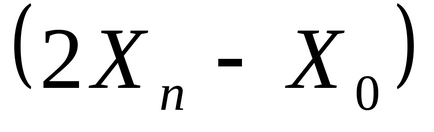
4. lépés: Ha a feltételek

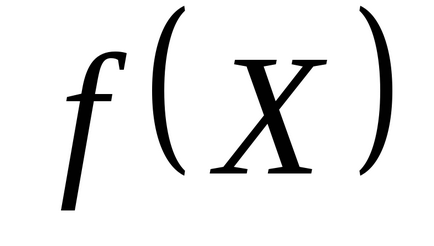
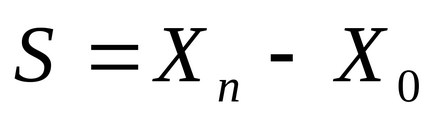
,
azaz irány
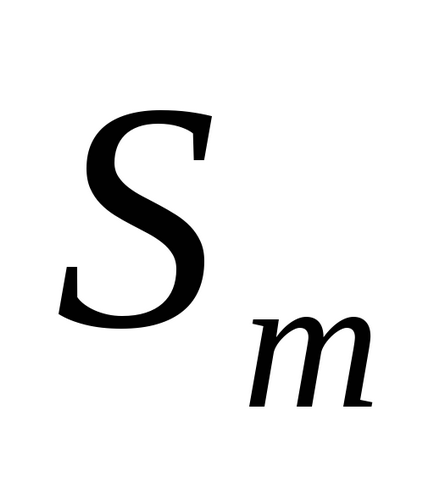

5. lépés: Ha
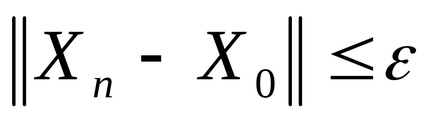
Példa. Az ikonra kattintva, hogy megnyitja a Mathcad dokumentum módszer konjugált irányok, amelyekben a számítások elvégzésére.
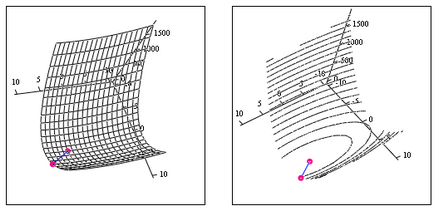
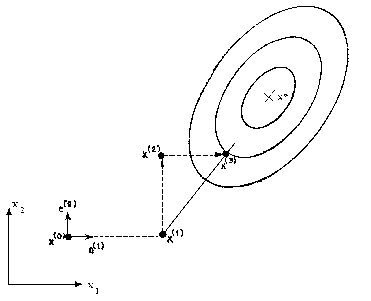
Eljárás konjugált irányok
Úgy tűnhet, irracionális, hogy elutasítja a legsikeresebb iránya az aktuális iteráció és új ígéretes tendencia az utolsó helyen, hanem az első. Mégis könnyen belátható, hogy a legsikeresebb trend valószínűleg kimerítette magát, és egy új, ígéretes irány nemrég használt egydimenziós optimalizálása és alkalmazni, hogy azonnal, nincs értelme, hiszen a promóciós egyszerűen lenni.
Powell bebizonyította, hogy a determináns a mátrix területek maximális, ha, és csak akkor, ha az irányt

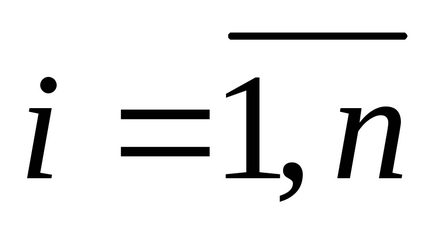
Ez azt bizonyítja, hogy a Powell eljárás konvergál a pont, ahol a gradiens nulla, ha az objektív függvény szigorúan konvex. Ez a pont egy lokális minimum. A módszer nagyon érzékeny a megépítésére szolgáló eljárásra konjugált irányok és ezért függ a pontosság egydimenziós keresés használatos. Powell használatát javasolták sorozata másodfokú interpolációs speciális beállítások a sor keresési eljárást. Azonban numerikus vizsgálatok kimutatták, hogy a módszer a konjugátum irányok Powell nem szabad használni, amikor a dimenziója több mint 20.