A lehetséges az elektromos mező
Kezdjük egy vitát a potenciális energia, amely a töltés elektrosztatikus térben. Először is, meg kell emlékezni, hogy ez egyáltalán lehetséges, hogy a koncepció a potenciális energia semmilyen körülmények között.
3.4.1 A konzervatív erők
Az erőt nevezik konzervatív (vagy potenciális), amikor a munka ezen erő nem függ az alak a röppálya és esetben csak a kezdeti és a végső helyzetét a test.
Tegyük fel például, a test az intézkedés alapján konzervatív erők
Megmozdult a kezdeti
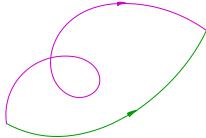
1 pont, hogy a végén a 2. pont (ábra. 3.16). Ezután a munkaerő
Ez csak attól függ a helyzet
maguk 1. és 2. pontjában, de nem a pályája test mozgását. Például pályákat 1. a. 2. és az 1. b. A 2 érték azonos lesz.
Ábra. 3.16. A koncepció a konzervatív erők
Megjegyezzük, hogy a munka konzervatív erő mentén bármely zárt pálya nulla. Sőt, menjünk ki az 1. pont a pálya 1. a. 2 és vissza hátra a görbe mentén 2. b. 1. Az első pálya teszi a munkaerő A, míg a második pálya egyenlő munkája A. Ennek eredményeként, a teljes munka nulla lenne.
Tehát, a koncepció a potenciális energia csak akkor léphet be abban az esetben, a konzervatív erők. A potenciális energia W egy matematikai kifejezés, amely függ a testet, oly módon, hogy a munkaerő egyenlő a változás a kifejezést egy mínusz jel:
Vagy ami ugyanaz:
A = (W 2 W 1) = W 1 W 2:
Amint látható, a munka konzervatív erő közötti különbség a potenciális energia számított értékek rendre a kezdeti és a végső helyzetben a test.
A konzervatív erőket, akkor az jól ismert. Például a gravitációs konzervatív. Rugóerő túl konzervatív. Ezért beszélhetünk a potenciális energia a test, emelt a föld felett, vagy a potenciális energia a deformált tavasz.
De a súrlódási erő nem konzervatív: a munka a súrlódási erő függ az alakja a pálya, és nem egyenlő nullával lezárt pályán. Ezért nincs ¾potentsialnoy a szervezet energia területén treniya¿ erő.
3.4.2 potenciális elektrosztatikus mező
Úgy tűnik, hogy az erő, amellyel az elektrosztatikus mező hat a töltött test és konzervatív. A munka ezen erő által végzett mozgó töltés, az úgynevezett munka elektrosztatikus tér. Van tehát a legfontosabb tény:
Működtetése elektrosztatikus mező nem függ az alak a pályákat, amelyen a töltés mozgatjuk, és határozza meg csak a kezdeti és a végső helyzetét a töltés. Field munkát egy zárt pályán nulla.
Ez a tény is nevezik potenciális elektrosztatikus mező. Csakúgy, mint a gravitációs mező, elektrosztatikus mező lehetséges. Működés az elektrosztatikus mező azonos minden utakat amely töltés lehet mozgatni az egyik fix pontot a térben a másikba.
A szigorú matematikai bizonyítása a lehetőségére az elektrosztatikus tér körén kívül az iskolai program. Azonban ¾na strogosti¿ fizikai szinten tudjuk ellenőrizni ezt a tényt a következő egyszerű érv.
Könnyen belátható, hogy ha nincs elektrosztatikus mező lehetséges, lehetséges lenne, hogy építsenek egy örökmozgó! Valójában, míg lesz egy zárt pályán, mozog a töltés, amely a területen pozitív lenne a munka (és így nincs változás a környező szervek nem történt volna meg). Twist díj ezen az úton felhívjuk korlátlan mennyiségű energiát a semmiből, és minden energia problémákat megoldani :-) De ez, sajnos, nem nézem nyilvánvalóan ellentmond a törvény az energiamegmaradás.
Mivel az elektrosztatikus tér potenciál, beszélhetünk potenciális energiája a díj ezen a területen. Kezdjük egy egyszerű és fontos ügy.
3.4.3 A potenciális energiáját díj egységesen területén
A potenciális energia a test, emelt a föld felett, az MGH. töltés esetén egységes mező tűnik, hogy nagyon hasonlít a mechanikai helyzetet.
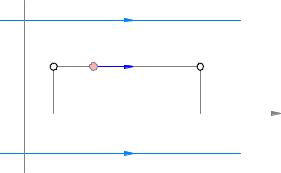
Tekintsünk egy egységes elektrosztatikus mező E, amely erővonal mentén irányul az X tengely mentén (ábra. 3.17). Tegyük fel, hogy a pozitív töltés q mentén mozgatják a tápvezetéket 1. pont (a koordináta x 1) a 2. pont (a koordináta x 2).
Ábra. 3.18. Mozgó díj egységesen területén
Mozgó 1. pont 2. pont, nézzük válassza útját 3. 1. 2, ahol a 3 pont fekszik azonos teljesítmény összhangban az 1. pontban Ezután a munka 32 az A szakasz 32 nulla, mert haladunk merőleges erő. Az eredmény:
A = A 13 + A 32 = A 13 = qE (x 2 x 1)
Látjuk, hogy a munka a területen csak attól függ a vízszintes kezdő és befejező pozíciókat a díjat. Feljegyezzük a képlet a következő:
A = qEx qEx 1 2 = ((qEx 2) (qEx 1)) = (W 2 W 1) = W:
Itt, W 1 = W 2 1. qEx = qEx 2. terepmunka, összhangban az (3.8) egyenlő a változást a jel mínusz a értéke
Ez az érték a potenciális energiája a díj egységesen elektrosztatikus mezőben. X jelöli az abszcissza a pont, ahol a potenciális energia kérik. A nulla szint a potenciális energia ebben az esetben megfelel a származási x = 0, és az ábrákon szemléltetett a szaggatott vonal merőleges a vonalak intenzitása 4.
Emlékezzünk, hogy míg a figyelembe vett q> 0 általános képlet (3.9), amely a töltés mentén mozgó távvezeték potenciális energia csökken a növekvő x. Ez természetes: elvégre a mező nem pozitív munkát, vezetési díjat, és a kinetikus energia a díj emelkedik csökkenése miatt a benne rejlő energiát.
Könnyen azt mutatják, hogy (3.9) érvényben marad q <0. В этом случае потенциальная энергия возрастает с ростом x. Это тоже понятно: ведь сила, с которой поле действует на заряд, теперь будет направлена влево, так что движение заряда вправо будет осуществляться против действия поля. Заряд тормозится полем, кинетическая энергия заряда уменьшается, а потенциальная энергия увеличивается.
Tehát egy fontos következtetés: a képlet a potenciális energia a töltés q algebrai érték (beleértve a jel), és nem a nagysága.
4. Valójában a nulla szint potenciális energia lehet kiválasztani sehol. Más szóval, a potenciális energia meghatározása csak akár egy tetszőleges adalék C konstans, t. E. W = qEx + C. Semmi baj ezzel a bizonytalanság nem: a fizikai értelemben is a potenciális energia is, és a különbség a potenciális energia egyenlő a munka területén. A C konstans E különbség csökken.
3.4.4 A potenciális kölcsönhatás energiája pont díjak
Tegyük fel, hogy a két pont díjak q 1 és Q2 vákuumban R távköznyire egymástól. Belátható, hogy a potenciális energiája azok kölcsönhatása az alábbi képlet szerint:
Vesszük az (3.10) bizonyítás nélkül. Két jellemzője ennek képletű kell vitatni.
Először is, ahol a nulla szint potenciális energia? Mivel a potenciális energia, mint láthattuk, a általános képletű (3.10) nullára nem tud forogni. De valójában nulla, és ez található a végtelenben. Más szóval, ha a díjak találhatók végtelenül messze egymástól, a potenciális energiája a kölcsönhatás értékét nullára (ez logikus ebben az esetben a díjak már ¾ne vzaimodeystvuyut¿).
Másodszor, q 1 és q 2 algebrai értéke töltse fel újra, azaz a. E. díjak tekintetében a jel.
Például, a potenciális energiája közötti kölcsönhatás két töltések pozitív lesz. Miért? Ha hagyjuk őket, szétszórja és eltávolítják egymástól. Kinetikus energiájuk növekszik, így a potenciális energia csökken. De a végtelenben potenciális energia nulla, és ha nullára csökken, akkor ez pozitív.
De a potenciális energiája kölcsönhatás ellentétes töltésű negatív. Valóban, nézzük távolítsa el őket egy nagyon nagy távolságra egymástól úgy, hogy a potenciális energia nulla, és megjelent. A díjak szétszórja, egyre közelebb, és a potenciális energia ismét csökken. De ha ez nulla volt, akkor hol alábbhagy? Csak negatív értékeket.
Egyenlet (3.10) is segít kiszámítani a potenciális energia rendszer díjak, ha a szám a díjak több mint kettő. Ehhez meg kell összefoglalni az energia mindegyik pár díjakat. Nem írunk általános képlet; jobban illusztráljuk ezt az egyszerű példát ábrán látható. 3.19.
Ábra. 3.19. A kölcsönhatás a három díj
Ha a díjak q 1. q 2. q 3 vannak oldalú háromszög a, b, c, akkor a potenciális energia kölcsönhatás: