Oldja meg a rendszer trigonometrikus egyenlőtlenségek
4. Keresse meg a legnagyobb egész megoldása egyenlőtlenséget:
Szorozzuk mindkét oldalán egyenlőtlenség 15 - a legkisebb közös nevező Ezen frakciók. Kapjuk az egyenértékű egyenlőtlenséget:
3 · (X-2) -5 · (2x + 3)> 15. Nyilvánosságra zárójelben: 3x-6-10x-15> 15 és egyszerűsítése:
3x-10x> 15 + 6 + 15. Kapunk -7x> 36. Osszuk mindkét oldalán az egyenlőtlenséget a negatív együttható x, így az egyenlőtlenség előjellel:
x<-36/7. Выделим целую часть и покажем решения неравенства на числовой прямой.
A legnagyobb egész szám kikelt ideig - ez a szám -6.
5. Határozza meg a helyes döntés egyenlőtlenséget: log2 (x-4) ≤3.
Ábrázoljuk a száma 3 logaritmusban bázis 2.
log2 (x-4) ≤ log2 március 2; így log2 (x-4) ≤log2 8. Mivel a logaritmikus függvény a bázis 2 növekszik a beállított pozitív egész számok, az utóbbi egyenlőtlenség lenne elvégezhető a feltétellel, hogy x-4≤8, de ugyanakkor: X-4 > 0. Az első feltétel magában foglalja: h≤12, és a második, hogy x> 4. A közös érték h∈ (4; 12].
7. Enter funkció grafikon látható az ábrán.
Az ábrán látunk egy parabola, amely lehet meghatározni a következő egyenlettel: y = a (x-m) 2 + n, ahol (m, n) - a koordinátákat a csúcsa a parabola. Ábra parabola vertex - dot (2, 1). Ezért, m = 2; n = 1. És mi a helyzet az együttható a. Megnézzük választ: mindenhol tényező, mielőtt a konzol egyenlő eggyel. Nos, rendben - kevesebb gond! Mi kapott képlet: y = (X-2) 2 +1.
11. A hossza a téglalap alakú rész 120 m, és a szélessége 75% hosszának. 35%, a szántott terület, míg a nem szántott:
A hipotézis, a szélesség 75% -a 120 m - a szelvény hossza. Ez 3/4 hosszúságú, azaz, 120: 4 · 3 = 90 méter. A területet a téglalap alakú részének hossza egyenlő a terméket rész szélessége, azt jelenti, 120 m · 90m = 10800 m 2 eke 35%, ezért nem felszántott 100% -35% = 65%. Továbbra is találni 65% -a 10800. Kérjük százalékos tizedes törtet: 65% = 0,65, és szorozza meg frakcióból 10800.
0,65 · 7020 = 10800. A válasz arra a kérdésre, a problémát: nem szántott 7020 m 2.
12. egyenlet megoldásához:
A fő logaritmikus azonosság alkalmazható jobb oldali:
Kaptunk azonos mértékben, hogy az alap 2, következésképpen, a teljesítmény e fok egyenlő. Másodfokú egyenlet kapjuk: x 2 + x = 2, vagy X 2 + x-2 = 0. A tétel Wyeth válasszuk gyökerek: x1 = -2; x2 = 1.
14. egyenlet megoldásához: sin 2 x-cos 2 x = cos (x / 2).
Dupla szög koszinusza képlet: cos2α = cos 2 α-sin 2 α, Ha ez az egyenlet átalakul:
-cos2h = cos (x / 2) ⇒ -cos2h-cos (x / 2) = 0 ⇒ cos2h + cos (x / 2) = 0. Az összeg a koszinusz transzformációt, hogy a munka, a következő képlet segítségével:
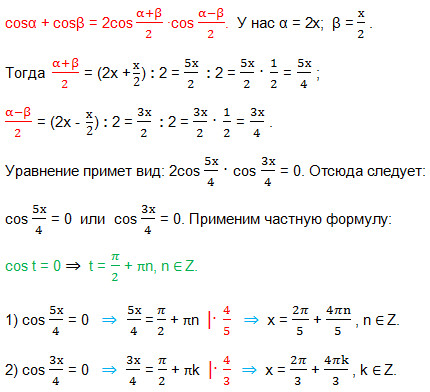
17. helyek keresése ordináta mennyiségű szélsőérték az f (x) = x 3 / (x 2 -3).
Természetesen, ha tudjuk, hogy a szélsőségek - minimum és maximum funkciók, melyeket csak a kritikus pontokon. A klasszikus megoldás erre a küldetés: 1), hogy megtalálja a származékot ezt a funkciót; 2) megtalálja a kritikus pont, és jelölni azokat a számegyenesen; 3) meghatározzuk a jel a származék a hiányosságok kritikus pontokat; 4), hogy megtudja, mik a kritikus pontok minimális pontok és a maximális képpont; 5) keresni függvény értékei ezeken a pontokon a legkisebb és a legnagyobb -, amely összehangolja szélsőérték pont; 6) adja ki ezeket az értékeket a koordinátáit. De ebben a konkrét munkát sokkal könnyebb! A funkció adott nekünk furcsa, azaz az összes lehetséges értékének x, a következő egyenlőség: f (-x) = f (x). Graph páratlan függvény szimmetrikus az eredetét. Mit jelent ez, és hogyan segít ez nekünk? Azt állítják, hogy ha ez a funkció maximum a pont abszcissza a. az ő szimmetrikus pont abszcissza (ok), akkor minimális. Ismét függvény értékei ezeken a pontokon a és s is ellentétes számokat. És mi az az összeg, ellenkező egész? Ez így van: nulla. Következtetés: ha meg kell találni az összeg az y-szélsőérték páratlan függvény, akkor a válasz: 0.
21. Keresse meg az összeget a gyökerek egyenlet: x -2 16x -1 -80 = 0.
Azt, hogy a szubsztitúció: x -1 = y. Megkapjuk a egyenletet használva: y 2 -16y-80 = 0. Find a gyökerek: y1 = -4, és y2 = 20.
Ezután X -1 = -4, vagy x -1 = 20.
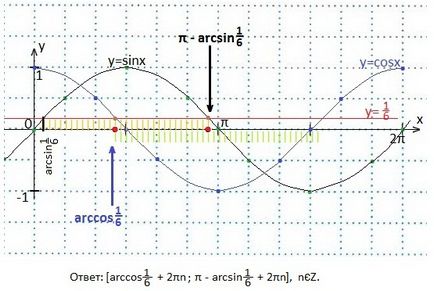
22. Oldja meg a rendszer egyenlőtlenségeket:
Egy koordináta-rendszerben építünk grafikonok a funkciók y = sinx, y = cosx és y = 1/6. Mi határozza meg az intervallum x értékei, ahol a szinusz görbe felett van, és a vonal alatt grafikon koszinusz y = 1/6.
24. Find területének egy ABCD paralelogramma, ha A (5; 4), B (0, 3), C (4, 7), D (9; 8).
Terület paralelogramma megtalálják a képlet: S = absinA, ahol a = az AD és b = AB - oldalán a paralelogramma, A - közötti szög ezen oldalán. Vektorok felhasználásával: megtalálni a koordinátákat és vektorok modulok kifejező fél AD AB paralelogramma koszinusza közötti szög ezen vektorok. Ezután keresd meg a sine a szög, és a képlet területén paralelogramma helyettesíti az összes szükséges értéket.

25. A elektronikus óra mutatja az időt órákban és percekben (0:00-23:59). Hányszor naponta látható a kijelzőn 4 számjegy 2, 0, 1, 9 (bármilyen sorrendben). Mivel nincs, mint 91 perc vagy 29 óra, a kombinatorika nem segít nekünk. Csak megy összes lehetséges valós idejű mérés.
Barátok, ismételje meg a képletet. Sok sikert kívánok!