Kezdet „Euclid

1. modell posztulátumain Eukleidész rendszerének

Posztulátumok 1-3 meghatározza a lehetőségét vonalzó konstrukciók (osztás nélkül) és iránytűk. Érdemes tisztázni, hogy a „közvetlen” Euclid megérti „korlátozott” sort, azaz a modern terminológia, a szegmens.

A matematikusok már többször fellebbezett a rendszer posztulátumok és Euclides próbál javítani. Tehát, a XVIII. kiderült, hogy a tétel 4 felesleges, mivel ez következik a többi axiómák és feltételezi.

Hasonló vizsgálatokat végeztünk sokáig, és az 5-ik posztulátum továbbá, hogy azért van, mert a bonyolult nyelv tűnt sokkal kevésbé nyilvánvaló, mint a többi posztulátumok és axiómák. Megpróbálták bizonyítani alapján a fennmaradó posztulátumok és axiómák. Ebben az esetben, csak hogy megtudja, hogy az 5. posztulátum logikailag egyenértékű más nyilatkozatot (azaz, hogy lehet belőle származik, és a másik kezét, és származhat bármelyik, ha azt feltételezzük, hogy már létre), de sem ő vagy az állításai nem bizonyított alapján más posztulátumok és Euclides. Elképzelhető geometriát, amelyben az 5-edik posztulátum nem teljesül, és a fennmaradó posztulátumok és axiómák teljesülnek (Lobachevsky geometria). Jellemzően a modern veszi a geometria az 5. posztulátum helyébe annak megfelelő párhuzamos posztulátum (már megtalálható Proclus az V. században ...) ponton keresztül nem adott vonalon, akkor dolgozzon csak egy egyenes vonal, amely nem metszi ezt. (A „közvetlen” itt, mint általában a modern matematika, képviseli a végtelen egyenes vonal).

2 Modell Az axióma párhuzamosság

Felsorolja az euklideszi axiómák különböző fennmaradt ókori példányban a „Elements” eltérnek egymástól -, és nem az egészet adott axiómák (és posztulátumok) tartozik Euclid. A leggyakoribb az alábbi listából az axiómák.

Egyenlő egy és ugyanaz, és egyenlő egymással.

És a két vonal nem tartalmazhat szóközt.

Természetesen felmerül a kérdés merül fel, amikor találkozott a posztulátumok és Euclides, - a tanait eltérnek axiómák. Általánosságban úgy tűnik, hogy az axiómák, ellentétben posztulátumai vonatkoznak nagyon általános tulajdonságait mennyiségű változatos jellegét, r. H. Pl számok, nemcsak a geometriai objektumok. Azonban az axióma 9 ellentmond ennek az értelmezésnek. A jelentése ennek axiómának -, hogy a két szegmens nem konvergál két különböző pontban - azaz korlátozzák néhány ábra véges területen.

Ábra. 1. A kilencedik axióma Euclid

Most már megfogalmazott ezt az axiómát a következőképpen rendelkezik: „Két pont tartják legfeljebb egy sort.” Próbáld megérteni, hogy mi a különbség az axiómák posztulátum 1?

1 állítja posztulálni létezését legalább egy szegmenst a végei két adatpont és axiómát 9 - hogy az ilyen szegmensek nem több, mint egy.

Fontos szerepet játszik az axióma 7. Tény, beszélünk róla, hogy ha elő az egyik alak a másik, hogy azok egyeznek, akkor ezek a számok egyenlő lesz. Euclid mindig használja a „egyenlő” abban az értelemben, hogy az egyenlő terület, azaz a. E. Egyenlő tér (hossz, térfogat, szög, mennyiségek). A modern értelemben vett „egyenlő”, mint alkalmazott geometriai ábrákkal pontosan azt jelenti, „match bevezetésére”: azonos számok különböznek csak a helyét (vagy inkább az egyenlőség azt jelenti, hogy van egy mozgalom, amely átalakítja az egyik alak egy másik, a mozgás jelentette átalakulás, amely megőrzi a távolságot ha a szám volt szilárd, és tudtuk mozgatni). Már XVII századi matematika. egyenlőség érteni ebben az értelemben; Leibniz az ilyen egyenlőséget bevezetett egy speciális kifejezés - összhangot. Annak érdekében, hogy axióma 7, modern értelemben azt jelenti, hogy azonos (egybevágó) számok egyenlő területű. (Ez természetesen az egyenlő darabokra nem kell egyenlő).

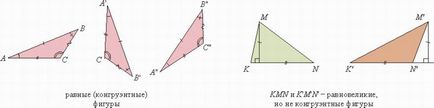
Ábra. 2. Ekvivalens és szabályos alakú

Az „összehangolás” Euclid azt bizonyítja, amit most hívott a jelei az egyenlő háromszögek, de a jövőben kerüli nyomvonalakat, hivatkozva a bizonyítéka egyenlőség egyes számok a már bevált jelei egyenlő háromszögek.

Általánosságban, a választás a axiómák és posztulátumok Euclid sikeres, de a rendszer nem teljes: hiányzik belőle néhány fontos axiómák (pl sztereometrikus). Ugyanakkor Arisztotelész úgy vélte, hogy időnként bemutatni a tudomány hallgat bizonyos tulajdonságait és rendelkezések miatt szembetűnőség. Lehetséges, hogy Euklidész nem célja az, hogy egy teljes listát a jóváhagyások szükséges további bizonyítékokat. Ez a feladat elhagyta, majd matematikus.