hibafüggvényt

előző ◈ a következő

Ez igaz (és a sorozat konvergál) minden valós x. és az egész komplex síkon. szerinti arány vizsgálata. Sequence nevezők formák sorrendben A007680 OEIS-ben.

hibafüggvény végtelenben egyenlő egy; de ez csak akkor igaz, ha a végtelenhez közelít mentén valós tengelye, mivel:

Ha figyelembe vesszük a hibafüggvényt a komplex síkban z = ∞, neki lényeges szingularitás.

A származék a hibafüggvény származik közvetlenül a meghatározás:

d d x EMA x = 2 π e -. X 2> \, \ operatorname \, X = >> \, e ^ >>.

Inverz hiba funkció egy sor

EMA - 1 x = Σ k = 0 ∞ c k 2 k + 1 (π 2 x) 2 k + 1 ^ \, x = \ sum _ ^ >> \ left (>> x \ right) ^,>

Ezért egy sor lehet az alábbi képlettel ábrázolható (megjegyzés, hogy a csökkentett frakció):

A szekvenciákat a számláló és nevező vágás után - A092676 és A132467 az OEIS-ben; szekvenciájának számláló csökkentésére - A002067 az OEIS-ben.

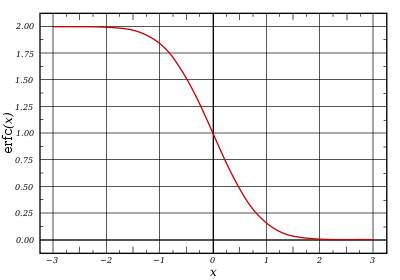
További hiba függvény

hibafüggvény és kiegészítő hibafüggvény található a megoldás néhány differenciálegyenletek, mint például a hő egyenlet peremfeltételek leírt Heaviside függvény ( „lépés”).

A digitális optikai kommunikációs rendszerek, bit hibaarány is fejezhető ki, amely a hiba funkciót.

A nagyméretű x hasznos aszimptotikus sor a komplementer hiba funkció:

Noha bármely véges x, ez a sorozat divergens, a gyakorlatban az első néhány tag elegendőnek kiszámításához ERFC x \ x>, jó pontossággal, míg a Taylor-sor konvergens nagyon lassan.

Egy másik közelítés a következő képlet adja

Inverz függvény Φ. ismert, mint a normális kvantilis függvény néha probit> és fejeződik ki a szokásos hiba funkciót, mint egy

Normál eloszlás gyakrabban használják az elmélet a valószínűség és a matematikai statisztika, míg az hibafüggvényt egyre inkább használják a matematika egyéb területein.

error függvény egy speciális esete az MittagLefflernek. és ez is képviseli, mint egy degenerált hipergeometriai funkció (funkció Kummer):

Hiba funkció is kifejezve a Fresnel integrál. Ami a szabályossá hiányos gamma-függvény a P, és a hiányos gamma-függvény,

Általános hiba függvény

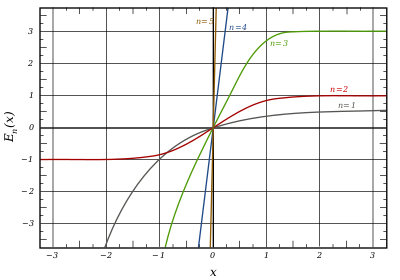
Jelentősebb speciális eset:

Miután elosztjuk n. Minden E n> páratlan n nézd hasonló (de nem azonos). Minden E n> n is, még hasonlítanak, de nem azonos, miután elosztjuk n. . Minden generalizált hibafüggvény n> 0 hasonlóan néz a féltér x> 0.

A fél-tér x> 0 minden általános funkciókat lehet kifejezni a gamma-függvény:

Ezért tudjuk kifejezni a hiba függvényében gamma-függvény:

Iterált integrálok a komplementer hiba függvény

Iterált integrálok a komplementer hiba függvény definíciója a

i n ERFC z = ∫ z ∞ i n - 1 ERFC ζ d ζ. \, \ Operatorname \, z = \ int \ határok _ ^ i ^ \, \ operatorname \, \ zéta \, d \ zéta.>

Ők lehet bővíteni egy sorozat:

ami azt jelenti, a szimmetria tulajdonságok

A nyelv a Java java.lang.Math tartalmaz egy szabványos könyvtár matematikai függvények [1] hibafüggvényt. EMA osztály megtalálható a csomagban org.apache.commons.math.special nem szabványos könyvtár szállított [2] Apache Software Foundation.

A Python, egy függvény hiba áll rendelkezésre [3] a standard matematikai könyvtárat. verziótól kezdődően 2.7. Továbbá, a hiba funkciót, a kiegészítő hibafüggvényt, és sok más sajátosságai modulban meghatározott különleges SciPy projekt [6].

A nyelv Erlang hiba funkció és a kiegészítő funkció hiba ről egy szabványos modul matematikai [4].

Kapcsolódó cikkek

előző ◈ a következő