Az eredete matematika 1950 Depman

Matematika az ősi népek

Középpontjában a matematika fejlődése, valamint bármely más tudomány, feküdjön kérdések gyakorlati emberi tevékenység.

„A megjelenése és a tudomány fejlődése miatt a termelést” - olvassuk Engels. - „Mint minden más tudományok, matematika alakult ki az emberek igényeit: mérésével földterületek és a hajók a időszámításait és mechanika.” *

* (Engels. Anti-Dühring. Gospolitizdat. 1948 o. 87.)

Ez a rendelkezés megerősíti a munka a nagy orosz matematikus Csebisev Pafnuty.

Egyiptomi hieroglifák felirattal és annak jelentősége

Legeredetibb, teljesen új matematika az idő, az ötlet merült fel egy tanulmány tökéletlenségek szélmalmok, a különböző gyári beállításokat, tisztán gyakorlati feladatok megoldásokat.

Egyértelmű, hogy minden tudomány kinő gyakorlatban táplálják és ellenőrzik.

Bizonyos matematikai ismeretek nőtt ki a gyakorlati emberi tevékenység, a megfigyelő a természeti jelenségek nekik susche * frissítik magukat a különböző népek az ókorban.

A „skála” írt az egyiptomi hieroglifák

Jelenleg ismerjük a matematikai tudás az ókori Babilon lakói (egy része a mai Irak) és az ősi Egyiptom (Nílus).

A legmagasabb a fejlesztési tevékenységek e népek, hogy létrehoz egy matematika elérte a négyezer évvel ezelőtt.

A legtávolabbi idők, a gyakorlati tevékenység az emberek nem nélkülözheti a matematikai részleteket. ez az információ felhalmozott több ezer éves, abban az időszakban, amelynek nincsenek írásos feljegyzések.

De a történelmi kor az élet különböző népek, van nagy korszaka, hogy nem engedélyezte a nevét bölcsek és tudósok, és a kutatás, mint a matematika, a teljesítmény csak annak tulajdonítható, hogy az egész nép, a gyakorlati tevékenység.

Először is meg kell, hogy meséljen a legfontosabb matematikai problémák az ókori Egyiptomban.

A modern tudomány egy viszonylag kis számú egyiptomi matematikai dokumentumokat. Jelenleg csak mintegy ötven.

Egyiptomi hieratikus, hogy egyszerűbbé, levél

A legrégebbi műemléke egyiptomi matematika az úgynevezett „Moszkva papirusz”, utalva az időszak körülbelül 1850 évvel időszámításunk előtt.

Ő szerezte meg az orosz gyűjtő Golenyiscsev 1893-ban és 1912-ben lett a tulajdonság a moszkvai Szépművészeti Múzeum.

Geometriai probléma a moszkvai papirusz. A feltüntetett majdnem négyszögletes, trapéz, amely megfelel a értelmezéseket az orosz matematikai kéziratok

Ez papirusz között más problémákat oldják meg a problémát kiszámítása a kötet egy csonka piramis négyzet alapú. Az ilyen problémák nem találtak más egyiptomi műemlékek. Ez az emlékmű tanulmányoztuk a szovjet tudósok - akadémikusok VA Turaev és VV Struve.

Térfogat nagyobb Moscow Rhind-papirusz, talált és szerzett az angol gyűjtő Rhind 1858-ban, ezért gyakran nevezik a Rhind papirusz. Tartozik a korszak ie 1700. Az orosz, írta le VV Bobynin *.

* (VV Bobynin. Matematika az ókori egyiptomiak. Moszkva, 1882. (Revision a Journal of az Oktatási Minisztérium 1908-ban)

Papyrus ez egy sávot 20 méter hosszú és 80 cm széles.

Ez azt mutatja, példákat a problémák megoldásához a mező számtani, geometria és algebra.

Minden más matematikai lapok Egyiptom, melyek közül az utóbbi utal az ezredik évben korunk ismételje meg ugyanezt a számítási szabályok, amelyek már az alapvető eszközök.

Kiderült, hogy az egyiptomiak négyezer évvel ezelőtt megoldotta sok probléma van a matematika gyakorlati (számtani, geometria, az első fokú egyenlet). Számba vették a decimális számrendszerben tulajdonában lévő számításokat lebegőpontos számok.

Fémhulladék Rhind-papirusz

A feladat, amit megoldani segítségével első fokú egyenletek, ezek megoldható oly módon, hogy az iskolában az úgynevezett „feltételezésekkel út” (ezt a technikát használták a XVIII században, a számtani minden nép néven „módszer a hamis pozíció” vagy „hamis szabály”).

Egyiptomiak megoldott és kihívások a haladást. Képesek voltak területének kiszámítására egyenes vonalú formák, és a tartomány; arány a kerülete és átmérőjének - mi száma π - a szabályok szerint az egyiptomi geometria egyenlő 3,10; egyes kutatók szerint az egyiptomiak tudták szabály kiszámításához a kötet egy gömb, és, persze, tudom, hogyan kell kiszámítani a kötet egy csonka piramis négyzet alapú.

Ezzel párhuzamosan a születési matematika Egyiptom lakói az ókori Babilon - sumérok - létrehozták a saját matek. Sumérok írt jelek, kötőjelet álló ék alakú, agyagcserép, amely szárítás után a tűző napon szerzett nagyobb erőt. Jelenleg ezek a több ezer agyaglap ásatások során.

Leningrádban, az Ermitázs és a moszkvai Szépművészeti Múzeum is számos egyiptomi és babilóniai emlékek autentikus feliratokat. Egyiptomi feliratok megőrizték és szfinxek álló Leningrádban a bankok a Néva folyó előtt a Művészeti Akadémia.

Az elmúlt húsz-harminc évben, azt találtuk, és tanulmányozta a hatalmas mennyiségű matematikai babiloni emlékek.

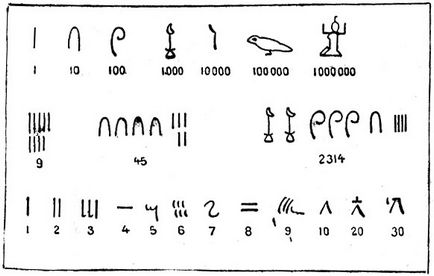
Egyiptomi számok: az első két sor volt írva hieroglifák; lényeg van írva hieratikus karakter

A tudósok találtak egy matematikai enciklopédia a babiloniak negyvennégy asztalok, képviselő, mintha egy összefoglalót minden matematikai eredményeket a sumérok a kora körülbelül kétezer évvel időszámításunk előtt, hogy van, az idő legnagyobb jólét a babiloni kultúra. E enciklopédia egyértelmű, hogy a babiloniak abban a távoli időben jobban gyakorlatban alkalmazott matematikai ismeretek, mint a görögök 1600 évvel később, bár még van néhány tudós szerint a görögök alapítói matematikai tudomány.

Probléma egyenletben rögzített hieroglifák. Olvasása jobbról balra: 'Pile (ismeretlen), 2/3, 1/2, 1/7, az egész 33', vagyis x + 2 / 3x + 1 / 2x + 1 / 7x = 33

A babiloniak voltak az alapítók a tudomány csillagászat. Ezek a megfigyelések alapján a görög csillagászat; közülük az, hogy egy hét napos hét, a szétválás a kör 860 fok, osztás 60 perc óra, perc 60 másodperc, 60 másodperc kétharmadát. Ugyanakkor babiloni asztrológia született - a képzeletbeli tudomány meghatározása a csillagok a jövő.

A babilóniaiak létre a tökéletes az idő számítás, amely alapján a 10-es számú nem, mint mi, és a 60-as számú, hogy sok esetben elősegítették a legnehezebb matematikai művelet - osztás.

Az általuk létrehozott rendszer a súlyok és intézkedések, amelyek várható előnyeit a mi metrikus rendszer (minden egyes intézkedés volt 60-szor nagyobb, mint az előző, ahonnan származik a szétválás a sarkok és intézkedések időben).

Ékírás a babiloniak

A babilóniaiak megoldható egyenletek másodfokú és néhány harmadik fokú egyenletek (az európaiak megtanulták, hogy megoldja az ilyen egyenletek csak a XVI század).

Babiloni agyagcserép

Mivel a második felében a második évezred kezdete előtt korunk területén között fekvő királyság Babilon, Asszíria és helyette az egyik kezét, és a Kaukázuson túli, másrészt, volt egy királyság Van vagy Urartu Királyság, amely a VIII században, ragadja meg a régióban a Dél-Kaukázus.

A népek Urartu, miután megtanulta a babiloni matematika, újratervezett azt. Megállapítást nyert, hogy beállnak a decimális számozás közel van a jelenlegi helyzeti decimális és drasztikusan eltér az egyiptomi decimális számozás, akik nem tudják a helyzetét elvet.

Urartui számtani nagyon hasonló az ősi örmény.

Így a matematika az ókori babilóniaiak által a nemzetek Urartu hatással volt a kultúra ősi matematikai kaukázusi népek, különösen az örmény, kizárólag előmozdítása korai virágzás.

Ezzel párhuzamosan Egyiptom és Babilon volt a matematika fejlődése Indiában.

Két vagy másfél ezer évvel időszámításunk előtt írták ősi hindu könyvek az úgynevezett Védák.

Ezekben a könyvekben, a változtatások az úgynevezett szútrák, részletes szabályokat tartalmaz a csere az egyik alak azonos területen, hogy egy másik szétválasztására és összecsukható ezek a számok.

Szabályai a Védák végeztük főként olyan derékszögű háromszög, amelynek oldalai vannak kifejezve egész számok. Védák ismertek integer derékszögű háromszögek a következő típusok:

1) oldala 8, 4b és hasonlók szorzatából a 3, 4, 5 az azonos számú;

2) oldala 5, 12, 13 és hasonlók;

3) oldala 8, 15, 17 és 12, 35, 37. A téglalap alakú háromszögek rendelkezik azzal a tulajdonsággal, hogy a négyzetösszegek a tér a átfogója a lábak (Pitagorasz-tétel). Ez a követelmény teljesül, ha a háromszögek a fenti számított a felek. Például:

12 2 + 35 2-144 + 1225 = 1369 = 37 2.

Építési formák más formában, ami pontosan megegyezik-ez és az ehhez kapcsolódó problémák, és lényeges részét képezik a görög geometria és tanult az iskolában természetesen.

A probléma a hajtogatási számok négyzet, háromszög vagy sokszög formájában négyzet tábla vagy tégla, amely helyére teszi az építési szakterületen, minden valószínűség, adott okot, hogy a tanításait háromszög, négyzet és általában sokszögszámok.

Háromszögű hívott számok: 1, 3, 6, 10, 15, és így tovább; tér - 1, 4, 9, 16, 25, és így tovább. Ha pontok ábrázolják tégla, ezek a számok jelentik a téglák száma létrehozásához szükséges háromszög vagy négyzet alakú fokozatos növelésével oldalukra, amint azt a rajzok:

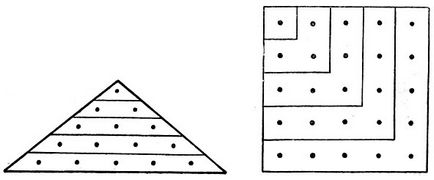
Szögletes lemezekre (tégla) az alapvető építőkövei Indiában és különösen vele szomszédos Babylon, teljesen mentes a kőből és fából. Izometrikus számadatok száma határozza meg ezeket a lemezeket.

Ez a gyakorlati feladat az épület art felhozott kérdését a meghatározása a szükséges lemezek száma, így háromszög, négyzet vagy sokszög alakú egy adott terület értékét.

Signature Ahasvérus ékírásos

Ez a feladat szükséges tanulási tulajdonságait természetes számok szekvenciák 1, 2, 3, 4. háromszög: 1, 3, 6, 10, 15. A tér: 1, 4, 9, 16. Ezek foglalkozott babiloniak, indiaiak és később - görög matematikusok, kezdve Püthagorasz.

Az életrajzok Püthagorasz (VI századtól időszámításunk kezdete) elmeséli tartózkodása Egyiptom, Babilon és India. Másrészt, annak tulajdonítják, hogy Püthagorasz annyi felfedezések terén a geometria és a több tudós, aki nem tudott tenni egy életen át.

Természetesen van egy elképzelés, hogy sok felfedezést tulajdonított Püthagorasz, ők hozták ki Babilonból, Indiában és Egyiptomban, különösen a tanítás a sokszög vagy rájött számok (háromszög, négyszög, és így tovább) kapcsolatos kérdéseket az épület art ezekben az országokban.

A legértékesebb hozzájárulása a kincset indiánok matematikai ismereteket az emberiség általunk alkalmazott rögzítési módszer segítségével a számokat tíz számjegy 1, 2, 8, 4, 5, 6, 7, 8, 9, 0.

Ennek alapján a módszer abban áll, a gondolat, hogy egy és ugyanaz a szám képviseli egység, több száz, vagy több ezer, attól függően, hogy milyen helyet foglal el ez a szám. Foglalt által meghatározott helyen a nullák tulajdonított a szám.

Az utolsó fejlesztés a helyi vagy pozicionális számrendszer, az ötlet az volt, a babiloniak, a legnagyobb érdeme a hinduk.

Francia matematikus Laplace (1749-1827) írt róla: „Az ötlet - hogy kifejezze az összes pár karaktert, így nekik más, mint az értéke az űrlap értéke azon a helyen, olyan egyszerű, hogy van, mert ez az egyszerűség nehéz megbecsülni, hogy mennyi ez elképesztő. ez nem könnyű, hogy jöjjön ez, látjuk tisztán példája a legnagyobb géniuszának görög tanulás - Arkhimédész és Apollonius, ahonnan ez a gondolat rejtve maradt. "

Nyitás a helyi számozási rendszer tette nem valami zseni. Ez a felfedezés, mint minden felfedezések az egyiptomiak és babiloniak, az eredmény egy hosszú fokozatos gazdagodását tapasztalat és megfigyelés az egész nemzet. Tehát sok látszólag nagyon absztrakt, a probléma a matematika.

A görögök, amelynek négy nagy kihívás, hogy az emberiség foglalkozik több mint két és fél ezer. Ezek a feladatok a következők:

1. Osszuk a kör vagy ív tetszőleges számú egyenlő részre (beépített kör szabályos sokszög tetszőleges számú oldalak).

2. Kettőzzék a kocka, hogy az, hogy létrejöjjön egy kocka, ami a térfogata kétszer magasabb, mint a kocka.

3. Osszuk bármilyen szögben három egyenlő részre.

4. Construct négyzet, amelynek területe megegyezik a terület a kör.

Mindezen feladatok megoldásához szükséges pontosan kizárólag vonalzót és iránytű, amelyen nincs szétválás.

Látszólagos egyszerűsége ellenére, nem voltak megoldható vonalzó és iránytű, amely jött létre csak a második felében a XIX.

Ezt megelőzően, részben azt követően, hogy sok ember, különösen a szerelmesek a matematika, nem komolyan tanulmányozta ezt a tudományt, időt és energiát egy hiábavaló kísérlet, hogy megoldja ezeket a problémákat.

A történelem ezeket a problémákat, mert meg van írva egy csomó könyvet, és brosúrák orosz lenne szükség egy külön könyvet, amelyből tanulni, mind eredménytelen kísérletet, hogy ki az elméd, ezek a látszólag nagyon egyszerű feladat lett nagyon fontos ága a modern matematika.