Meghatározása a súlypontok a sík szakaszok képződött hengerelt standard profilok és a

Home | Rólunk | visszacsatolás
Tárgy: A tömegközéppont.
A cél a munkát. Megtanulják felismerni a súlypontja bonyolult keresztmetszetek.
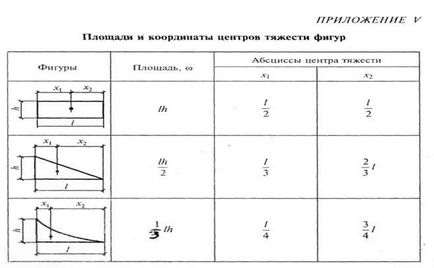
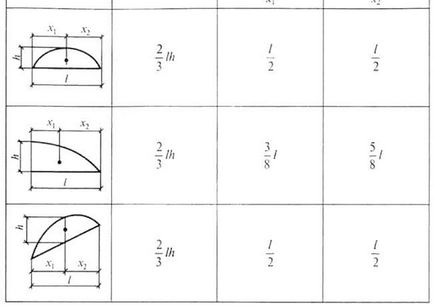
1. Szünet-szakaszt egyszerű formák. A problémák, mint szabványos alakú hengerelt profilok. Jellemzően hengerelt acél profilok képező részén, kijelölt 1,2,3 ....
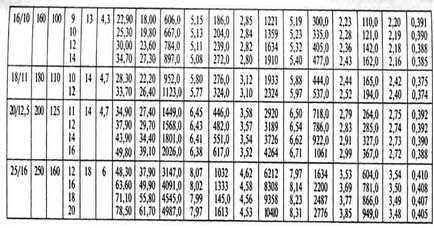
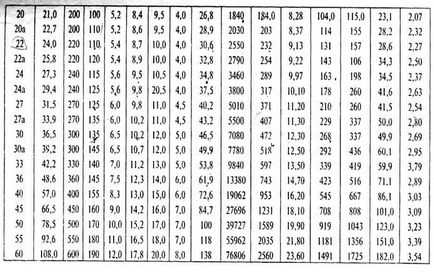
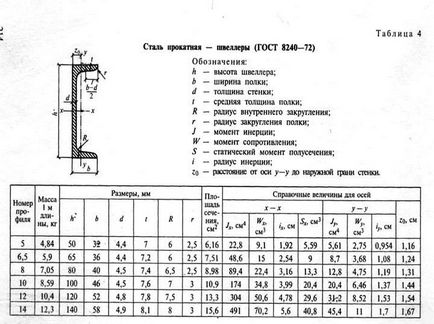
2. Jelölje meg a súlypontok az egyes profil (alak), és azt jelzik, hogy a C 1 C2 ..., Cn. Vélemények táblázat használatával (lásd. Prilozh.1).
3. Válassza ki a rendszer koordináta-tengely. Ajánlott az egyik koordinátatengelyek együtt a szimmetria tengelyével. A második koordináta tengely merőleges az első vezetőt, hogy áthaladt a súlypontok egy vagy több számok. Ha ez a származási egyeznek (vagy nem egyezik), hogy a súlypont a számok. A második tengely lehet irányítani úgy, hogy az áthalad az alsó (utolsó) metszéspontjából. Az első esetben a számítás egyszerűbb lesz.
4. Töltsük fel a képlet koordinátáinak meghatározására a súlypont a keresztmetszet:
Táblázatok segítségével felülvizsgálatok (lásd. App. 1), hogy meghatározzák a terület A1 hengerelt profilok. A2, ..., A n. x1 koordináták azok a súlypontok. x2, ... xn és y1. y2, ... yn képest a kiválasztott koordináta-tengely. A kifejezések száma a nevezőben és a számok a képletek számától függ a profilok által alkotott részén. A kapott értékeket behelyettesítjük a formulát és xc és yc.
Nem szabad elfelejteni, hogy ha az x tengely egybeesik a szimmetriatengely, a koordináta-YC = 0, és ha Y tengely egybeesik a szimmetriatengely, akkor xc = 0.
5. pont súlyponthelyzet az ábrán, azért, hogy egy bizonyos szinten, és megmutatja a távolságot a súlypont és a koordináta tengelyekkel.
6. Végezze érvényesítési megoldásokat, amely megváltoztathatja a helyzetét a koordináta tengelyek (vagy az ugyanazon a tengelyen), és segítenek megtalálni a koordinátákat a súlypont képest új tengelyt. A tömegközéppont nem attól függ, hogy a rendszer a kiválasztott koordináta-tengely.
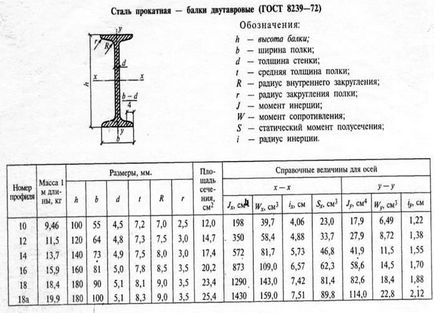
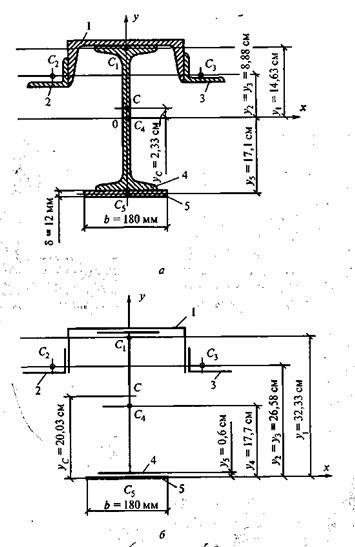
Példa 3.1. Határozza meg a súlypont koordináták szakaszok tagjai hengerelt szakaszok, amint az a 3.. A keresztmetszet áll egy I-gerenda № 33, csatorna № 27, két sarkok 90h56h6 mm, és egy lap részben 12h180 mm.
Megoldás 1. osztjuk a keresztmetszet összhangban hengerelt profilok és hagyja, hogy 1,2,3,4,5.
2. A táblázat segítségével állítsa be a súlypont az egyes profilok és hagyja, hogy C1. C2. C3. C4. és C5.
3. Mi választjuk ki a rendszer koordináta-tengely. Az y tengelyen kompatibilis egy szimmetriatengellyel, és irányítsa az x tengely merőleges az y tengelyen, és hordozzák a súlypontja az I-gerenda.
4. Mi írjuk a képletet koordinátáinak meghatározására a súlypont a keresztmetszet:
xc = 0, mert Y tengely egybeesik a szimmetriatengelye;
Mi határozza meg a területet, és a koordinátákat a súlypontok az egyes hengerelt profilok segítségével az asztal rész 2,3,4 App. 1
A5 = 1,2 · 18 = 21,6 cm 2;
y4 = 0, mivel az x tengely áthalad a súlypontja az I-gerenda;
Mi jelent a kapott értékeket a képlet meghatározására yc:
Nézzük a helyzetét jelzik a keresztmetszet súlypontja G (ld. 3).
5. Vizsgáljuk meg a megoldást. Döntetlen az x-tengelyen az alsó oldal a lemez (ábra. 3b.). Szögletes profilok változatlan marad, és a koordinátákat a súlypontok változása:
Határozza meg a helyzet a súlypont az új koordinátarendszerben
A különbség a koordinátáit a tömegközéppont egyenlőnek kell lennie a távolság a tengely x az első és a második oldat:
20,3-2,33 = + 1,2,
17,7 cm = 17,7 cm.
A: YC = 2,33 cm, ha az x tengely áthalad C4. és YC = 20,03 cm, amikor X tengely mentén terjed ki az alsó szélét.
Folytatása az asztal számát 1
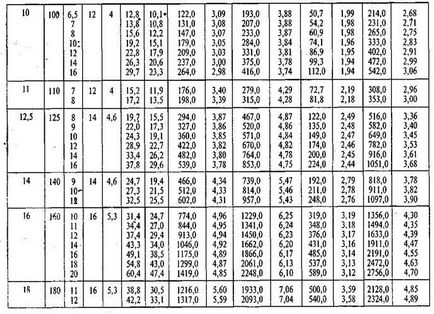
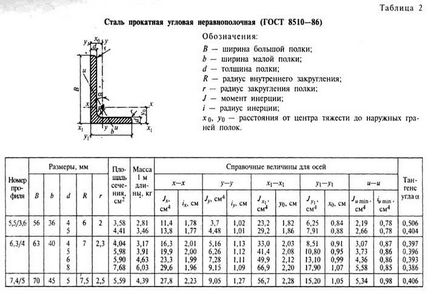
Táblázat folytatása 2 №