Elemzése és megoldása a feladat №5 OGE matematikai

grafikonok funkciók

Bár a vizsga, azt várjuk, hogy dolgozni grafikonok funkciók, azonban néhány megbízást kapott helyett rajz azok leírása. Ez úgy történik, hogy hangsúlyozzák a részleteket, hogy meg kell figyelni, hogy ha dolgozik, grafikus funkciókat.

Feladat száma 5 egyszerű, mégis utóbbi feladatokat kidolgozni, hogy az érdeklődő diákok valami gondolni.

A választ a feladat 5. számsor leíró összefüggés a különböző tárgyakat.

Elmélet a feladat №5

Mivel ezt a munkát beszélünk függvények és grafikonok, bemutatjuk az alapvető fogalmak és képletek.

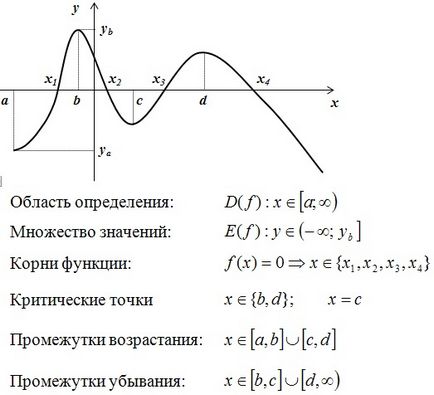
Önkényes például egy pillantást a tanulmány a funkció:

• tartomány és az értékkészlet
• gyökerek és kritikus pontok
• időközönként növekvő csökkenő

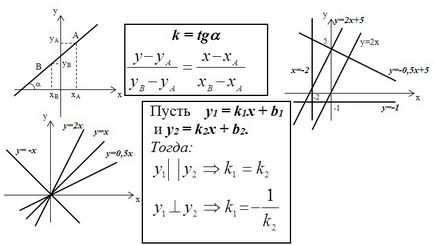
Most tekintsünk ezt az anyagot egy lineáris függvény:

ahol k - lejtő, b - konstans tag

Vegyük azt az esetet másodfokú függvényt:

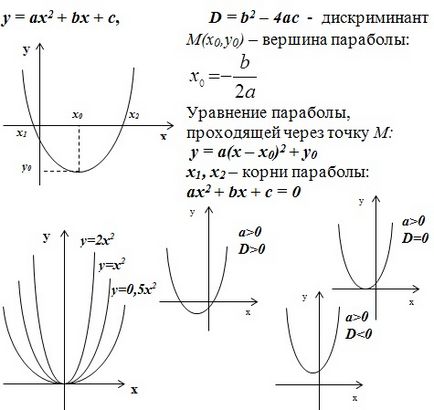
Azt, hogy ki a három esetben - az ügy a parabola és az olyan tényezők befolyása a formáját a parabola - az első példa. A második példában a szétszerelt hiperbola és általános minták függően általános formáját a grafikon egy matematikai kifejezés. A harmadik eset a direkt és változatai az építkezés, attól függően, hogy az együtthatók.

Elemzés modellváltozat №5 OGE matematikai megbízás

Az első referencia-kiviteli alak (parabola)

Az illusztrációk grafikonok funkciók

Egyezik a az együtthatók előjelei és c, és grafikonok a funkciók.

A) a> 0, c> 0

B) egy <0, c> 0

B) a> 0, c <0

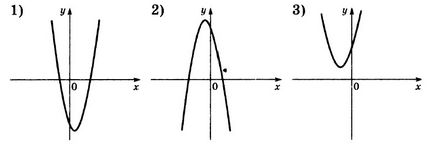
Emlékszünk a felelősséget a és b együtthatók az ábrázolási funkciók az űrlap

Együttható egy határozza meg az irányt a parabola ágai a: ha a> 0, akkor ága felfelé, és ha a <0, то ветви направлены вниз.

Így láthatjuk, hogy csak a második ága a parabola lefelé, majd egy <0.

Az első és a harmadik ág felfelé irányul, azaz az> 0.

Ezután megnézzük, hogy mi befolyásolja a koefficiens c.

A koefficiens c helyzetnek felel meg a parabola képest az X tengely, vagy a felelős a váltás a y-tengely, nevezetesen:

Ha c> 0, a csúcsa a parabola felett található az x tengelyen

ha c <0, то вершина параболы расположена ниже оси x

Így, az első parabola C <0, у второй и третьей c> 0.

Valamennyi fent, megtalálja a választ:

A második referencia-kiviteli alak (hiperbola)

Set közötti levelezés funkciók és grafikonok.

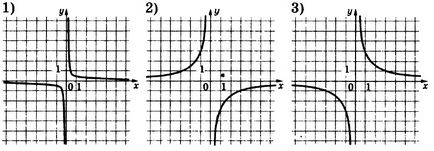
Ebben a helyzetben, akkor a két megközelítés - lehet irányítani általános szempontok, de akkor csak megoldani a problémát a helyettesítés. Azt javasoljuk, hogy megoldja a problémát az általános megfontolások és ellenőrizni cserélni.

• Ha az egyenlet a hiperbola pozitív (azaz, ha nem írja alá - mint a második és a harmadik eset), akkor a függvény grafikonját rejlik az első és a harmadik koordináta negyedévben
• ha mielőtt az egyenlet egy hiperbola egyik jele - (mint az első eset), akkor a gráf a második és a negyedik negyedévben

Így lehetséges, hogy azonnal meghatározza, hogy az első egyenlet felel grafikákat száma 2.

A második szabály, amit használni a következő:

• minél nagyobb a szám a nevezőben a hiperbola (a következő x), annál erősebb a hiperbola kapaszkodott a tengelyeket a koordinátasíknak

• Minél nagyobb a szám a számlálóban az egyenlet a hiperbola, a gyengébb és lassabb függvény grafikonját van nyomva, hogy a tengelyek

Következésképpen, a függvény B nekinyomódik a gyengébb tengelye, és megfelel a 3. ábrára, és a funkciók az 1. ábra szerint, mivel erősen nyomódnak a tengelyek.

A harmadik referencia-kiviteli alak (lineáris grafikon)

Set közötti levelezés funkciók és grafikonok.

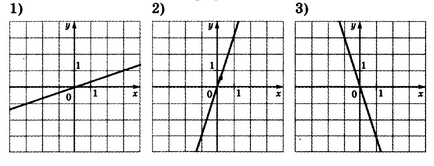
Funkció egy lineáris összefüggés, nevezetesen az első-rendű egyenlet formájában:

A grafikon ennek a funkciónak függ K és b.

• ha k <0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
• ha k> 0, a funkció növeli, azaz a vonal megy az alulról felfelé, mint az első két alak
• faktor b meghatározza az eltolás Y tengellyel, amikor b <0, то прямая пересекает ось y ниже 0 в точке y = b, если b> 0, a fenti nulla y = b
• Ha k> 1, akkor a vonal meredekebb, mint általában az y = x (mint a második és harmadik grafikon), ha k <1. то положе, как на примере рисунка №1

Ezért, grafikák y = 3x megfelel a 2. ábrának, mivel a vonal megy felfelé, és több, a meredek, mint a görbe az 1. ábrán, amely megfelel a függvény az y = (1/3) x.

A 3. ábra megfelel a függvénynek y = -3x Mivel a K = -3 <0, и график идет сверху вниз.

Az ötödik küldetés a demonstrációs verzió OGE matematikai rólunk szükség a következő:

Egyezik a grafikonok a funkciók és képletek, amelyek meghatározzák azokat.

A probléma megoldására van szükség, hogy tudja, hogy milyen típusú grafikonok a funkciók, amelyek a következők:

y = x² - parabola általában y = ax² + bx + c, de ebben az esetben, b = c = 0, és a = 1

X / 2 - egyenes, általában formájában egy grafikon egyenes y = ax + b, ebben az esetben, b = 0, a = 1/2

y = 2 / x - hiperbola, általában a grafikon y = A / X + b, ebben a példában b = 0, a = 2

Parabola ábrán látható A, hiperbola ábrán a B, és a vonal - B.