Összeadás és kivonás, vektorok
Az összeget két vektor \ (\ mathbf \) és \ (\ mathbf \) nevezik a harmadik vektor \ (\ mathbf \), és amelyet a \ (\ mathbf \) a végére \ (\ mathbf \), ha az elején a vektor \ (\ mathbf \) egybeesik a végén a vektor \ (\ mathbf \). Ezenkívül a vektorok végre a szabály alapján a háromszög vagy paralelogramma szabály.
\ (\ Mathbf = \ mathbf + \ mathbf \)
Összege több vektorok \ (\ mathbf \), \ (\ mathbf \), \ (\ mathbf, \; \ ldots \) az a vektor, \ (\ mathbf \), a kapott egymást követő hozzáadásával adatok vektorok. Egy ilyen művelet szerint végezzük a szabály a sokszög.
\ (\ Mathbf = \ mathbf + \ mathbf + \ mathbf + \ ldots + \ mathbf \)
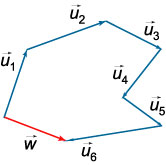
Kommutatív jog hozzáadás
\ (\ Mathbf + \ mathbf = \ mathbf + \ mathbf \)
Az asszociatív törvény hozzáadás
\ (\ Bal (+ \ mathbf> \ right) + \ mathbf = \ mathbf + \ left (+ \ mathbf> \ right) \)
Az összeg vektorok koordinátái
Amikor két vektor megfelelő koordinátákat adunk.
\ (\ Mathbf + \ mathbf = \ left (+, +, +> \ right) \)
A különbség a két vektor \ (\ mathbf \) és \ (\ mathbf \) az a vektor, \ (\ mathbf \), feltéve:
\ (\ Mathbf = \ mathbf - \ mathbf \), ha a \ (\ mathbf + \ mathbf = \ mathbf \)
A különbség vektorok \ (\ mathbf \) és \ (\ mathbf \) az összege a vektor \ (\ mathbf \), és az ellentétes vektor \ (- \ mathbf \):
\ (\ Mathbf - \ mathbf = \ mathbf + \ left (- \ mathbf \ right) \)
A különbség a két vektor egyenlő a nulla vektor.
\ (\ Mathbf - \ mathbf = \ mathbf \)
A hossza a nulla vektor nulla:
\ (\ Left | \ mathbf \ right | = 0 \)
Vector különbség a koordinátákat
Levonva két vektor megfelelő koordináta is levontuk.
\ (\ Mathbf - \ mathbf = \ left (-, -, -> \ right) \)