Funkciók és rekurzió a c - gyakorlat python Django
Funkciók és a rekurzió C ++

Nos, itt jön a végén a szilveszteri ünnepek, és velük együtt a képzés C ++. Mint említettük, azt kitüntetéssel végzett. Ma úgy a problémát a funkciók segítségével. A probléma részben megoldódik a használata rekurzív függvények. Emlékszem, hogy ezek a problémák felmerülésekor során Bevezetés a programozás (C ++) a steptic.org oldalon. Most egy kicsit megosztani a hírt, és kezdje el a feladatot.
Bit módosított helyszínen
-Írási funkciót min (a, b). kiszámításához legalább két szám. Ezután levelet min4 funkció (a, b, c, d). kiszámításához legalább 4 számjegy keresztül min funkciót. Tekintsük négy egész számot, és megjeleníti őket legalább.
A méret a bemeneti adat
Bevezetett négy egész számot.
A méret a kimenő adatok
A kijelző a válasz a problémára.
Mivel négy valós számok: $% x_1 $% $% y_1 $% $% x_2 $% $% y_2 $%. Írja meg a távolság függvényében (x1, y1, x2, y2). kiszámításához közötti távolság egy pont $% (x_1, y_1) $% és $% (x_2, y_2) $%. Tekintsük négy valós számok és az eredményt ez a funkció.
A méret a bemeneti adat
Bevezetett négy valós számok.
A méret a kimenő adatok
A kijelző a válasz a problémára.
Mivel két valós szám $% x $% és $% y $%. Ellenőrizze, hogy a pont tartozik a koordinátákat $% (x, y) $% teli négyzetek (beleértve a határ). Ha a pont tartozik a tér, kimeneti szó YES. egyébként nyomtatni a szót NO.
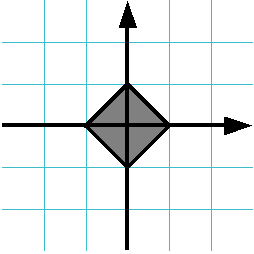
Az ábra nettó birtokában 1.
Az oldatot kell tartalmaznia IsPointInSquare funkció (x, y). return true. ha a pont tartozik a tér és hamis. ha nem tartozik. A program legfontosabb el kell olvasnia a egy pont koordinátáit, hogy hívja a funkció IsPointInSquare függően a visszaadott érték megjelenítéséhez a kívánt üzenetet.
IsPointInSquare funkció nem tartalmazhat az if.
A méret a bemeneti adat
Bemutatjuk két valós szám.
A méret a kimenő adatok
A kijelző a válasz a problémára.
Öt valós számok: $% x $% $% y $% $% x_c $% $% y_c $% $% r $%. Ellenőrizzük, hogy egy pont tartozik $% (x, y) $% kör középpontja $% (x_c, y_c) $%, és sugara $% r $%. Ha a pont tartozik egy kört, nyomtassa ki a szót YES. egyébként nyomtatni a szót NO.
Az oldatot kell tartalmaznia IsPointInCircle funkció (x, y, xc, yc, R). True. ha a pont tartozik a körbe, és hamis. ha nem tartozik.
A program legfontosabb el kell olvasnia a egy pont koordinátáit, hogy hívja a funkció IsPointInCircle függően a visszaadott érték megjelenítéséhez a kívánt üzenetet.
IsPointInCircle funkció nem tartalmazhat az if.
A méret a bemeneti adat
Bemutatjuk az öt valós számok.
A méret a kimenő adatok
A kijelző a válasz a problémára.
Ellenőrizze, hogy ezen a ponton tartozik az árnyékolt terület:
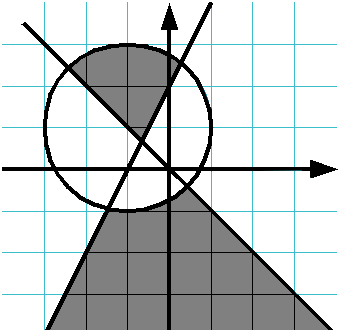
Ha a pont tartozik a régióban (a régió magában foglalja a határon), kimeneti szó YES. egyébként nyomtatni a szót NO.
Az oldatot kell tartalmaznia IsPointInArea funkció (x, y). True. ha a pont tartozik a régióban, és hamis. ha nem tartozik. A program legfontosabb el kell olvasnia a egy pont koordinátáit, hogy hívja a funkció IsPointInArea függően a visszaadott érték megjelenítéséhez a kívánt üzenetet.
IsPointInArea funkció nem tartalmazhat az if.
A méret a bemeneti adat
Bemutatjuk két valós szám.
A méret a kimenő adatok
A kijelző a válasz a problémára.
Adott egy valós pozitív szám $% a $% és tseloe szám $% n $%. Számítsuk $% egy ^ n $%. Megoldás készült egy funkciót teljesítmény (a, n).
A méret a bemeneti adat
Bevezetett egy igazi pozitív szám $% a $% és tseloe szám $% n $%.
A méret a kimenő adatok
A kijelző a válasz a problémára.
Adott egy pozitív egész szám, $% n> 1 $%. Vigyék ki a legkisebb osztó 1-től eltérő.
Megoldás készült egy MinDivisor funkció (n). Tranzakciók száma a programban arányosnak kell lenniük $% sqrt $%.
jelzés
Ha a szám $% n $% nem osztó, kevesebb $% n $%. száma $% n% $ - egyszerű, és a válasz a puszta száma $% n $%.
A méret a bemeneti adat
Bevezetett egy természetes szám.
A méret a kimenő adatok
A kijelző a válasz a problémára.
Adott egy pozitív egész szám, $% n> 1 $%. Ellenőrizze, hogy ez egyszerű. A programnak tartalmaznia kell, hogy a szó YES. ha a számos egyszerű és NO. ha a szám összetett.
Megoldás készült egy IsPrime funkció (n). amely visszaadja True prímszámok és összetett számok Hamis. Tranzakciók száma a programban arányosnak kell lenniük $% sqrt $%.
A méret a bemeneti adat
Bevezetett egy természetes szám.
A méret a kimenő adatok
A kijelző a válasz a problémára.
Hatványát is sokkal gyorsabb, mint a $% n $% szorzásra! Ehhez használja a következő rekurzív sorozat:
$% A ^ n = (a ^ 2) ^ $%, még $% n $%,
$% A ^ N = A × A ^ $%, páratlan $% n $%
Végrehajtja az algoritmus a gyors hatványozás segítségével rekurzív függvény.
A méret a bemeneti adat
Bevezetett egy valós számot, és egy nem-negatív egész szám $% n $%.
A méret a kimenő adatok
A kijelző a válasz a problémára.
feladat №10
Adott egy számsorozat, a szám megszűnik 0. Keresse meg az összeget az összes ezeket a számokat használata nélkül ciklust.
A méret a bemeneti adat
Sequence egész számok bevitele, megszüntetéséről száma 0 (self sorszám 0 nem tartalmazza, és ez szolgál jelzi a bezárás).
A méret a kimenő adatok
A kijelző a válasz a problémára.
feladat №11
Írása függvény FIB (n). amely az egész nem-negatív $% n $% hozam $% n% $ - e Fibonacci-szám. Ebben a feladatban nem használhatja hurkok - használja a rekurziót.
Az első és második Fibonacci-szám értéke 1, és minden következő az összege az előző kettő.
A méret a bemeneti adat
Bevezetett egy egész szám.
A méret a kimenő adatok
A kijelző a válasz a problémára.
feladat №12
Tekintettel az N. számának meghatározása módon lehet elhelyezni a táblán $% N × N $% $% N $% királynők nem üti egymást.
A méret a bemeneti adat
Ez tartalmaz egy számot $% N $%. $% (N ≤ 10) $%
A méret a kimenő adatok
A kijelző a válasz a problémára.