10-11 N
10. Elektromos kapacitás. kondenzátorok
Elektromos kapacitás félreeső vezetőt nevezett fizikai mennyiség egyenlő az arány a vezető tölteni a potenciális terén ennek fejében:
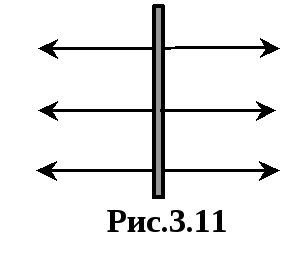
Villamos kapacitás karmester mutatja néhány díjat köteles tájékoztatni a vezetőt a potenciális vette a beállított értéket. Minél nagyobb a töltés vezeték, annál nagyobb a potenciális terén ez a díj. Ezért az elektromos kapacitás nem függ a nagysága a felelős vezető vagy annak potenciális értéke, de csak attól függ a mérete és alakja a karmester, és dielektromos tulajdonságainak a közeg, amelyben található. Egység vezető elektromos kapacitását SI nevezett farads (jele F 1):
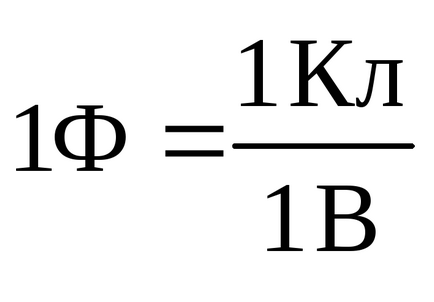
Tekintsük a meghatározása kapacitás a vezetőképes sugarú gömb R. található vákuumban. Erre a labda tájékoztatni fogjuk önkényes töltés Q töltés egyenletesen oszlik el a gömb felülete a felületi tömege
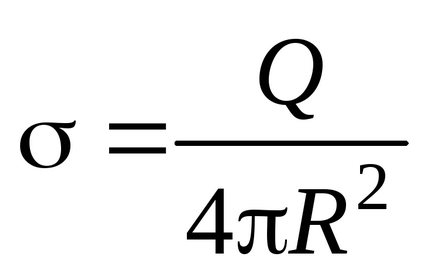
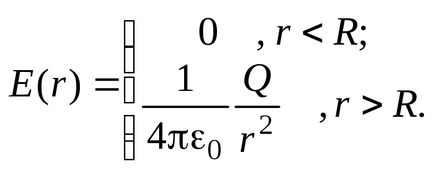
Részletek funkciók
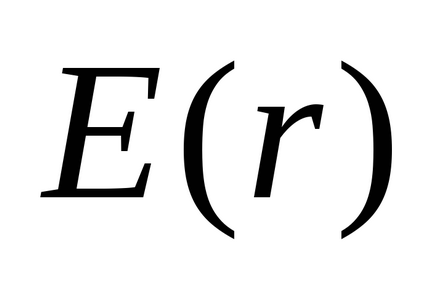
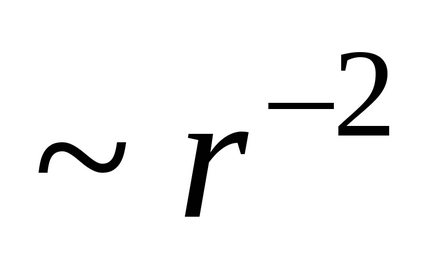
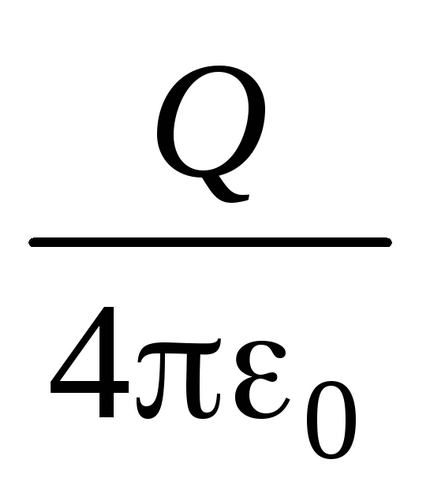
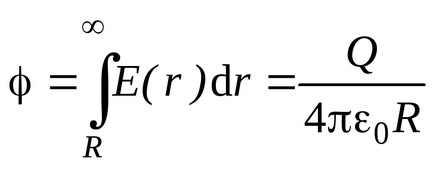
Összhangban (3.5) a labda konténer
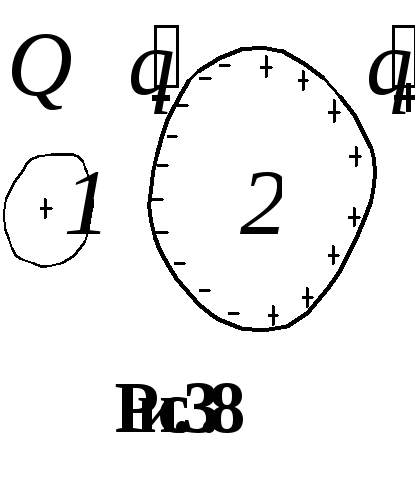
Elektromos kondenzátor kapacitása nevezzük fizikai mennyiség, egyenlő az arány a töltés kondenzátor a potenciális különbség által generált ez a töltés a területen közötti lemezek:
Ahogy a kapacitás a karmester, elektromos kondenzátor kapacitása nem függ a kondenzátor értéke díjat, sem a potenciális különbség a lemezek, és csak attól függ a mérete és alakja a kondenzátor és a dielektromos tulajdonságok a közeg kapacitás lemezek között. Meg kell jegyezni, hogy az elektromos kondenzátor kapacitása nem függ a jelenléte mellett a másik vezető vagy dielektromos szervek.
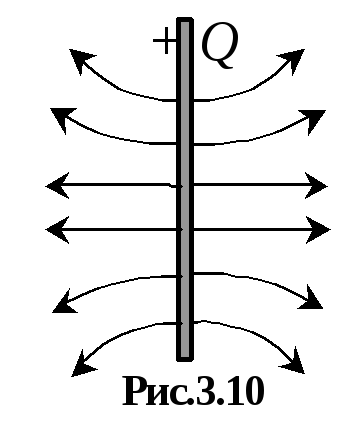
Példaként, mi származik egy általános képletű kapacitású lapos kondenzátor ábrán látható. 3.9 is. Definiáljuk az elektrosztatikus tér által termelt töltésű lemez terület S. erővonalait egy ilyen mező ábrán mutatjuk be. 3.10. Ha figyelembe vesszük, egy pont a térben helyezkedik el, közel a lemezt, hogy a távolság, hogy a lemez lényegesen kisebb, mint azelőtt, hogy határait (ezen pontok lemez fogja képviselni, mint egy végtelen nagy sík), a görbület a erővonalak a határokat a lemez lehet elhanyagolni (ábra. 3.11 ). Így egy végtelenül nagy feltöltött sík létrehoz egy homogén mező. Haladva a szimmetria a rendszer, a modul térerősség minden pontján egyenlő távolságra a lemez meg kell egyeznie, és az irányvektor

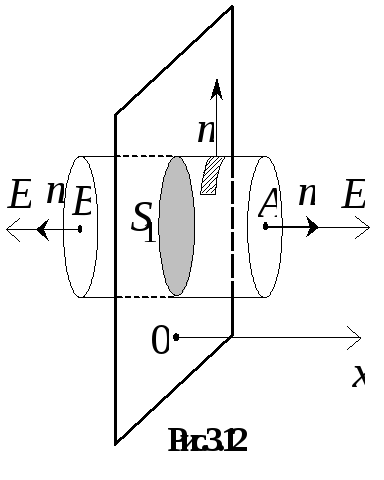
Mi határozza meg a térerő egy ponton koordináta x. mért tengelye mentén
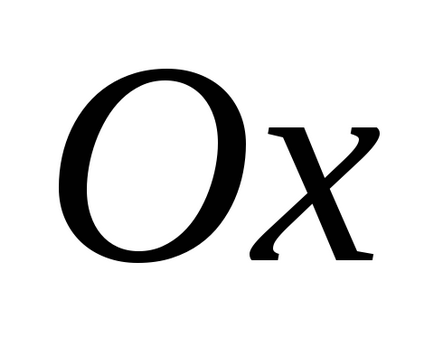
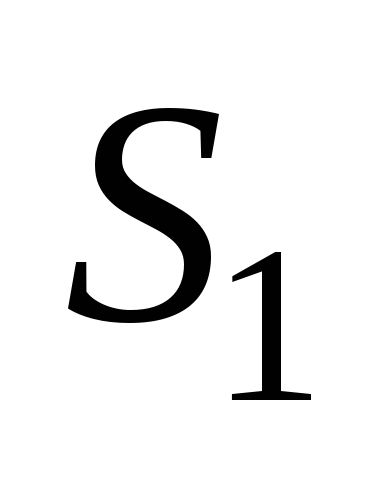

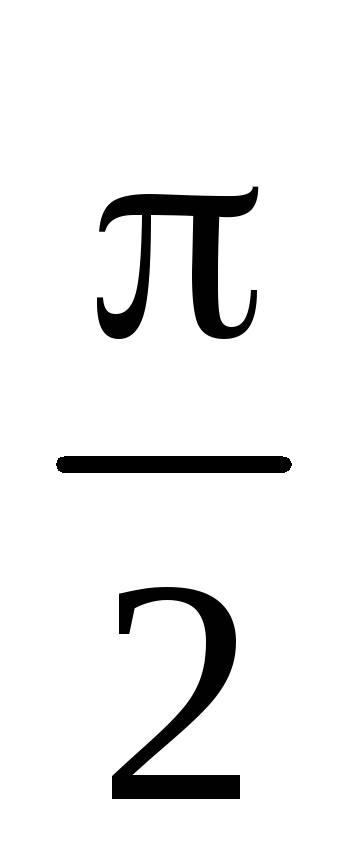
Határozza áramlási területen keresztül a kiválasztott felületre.
,
ahol
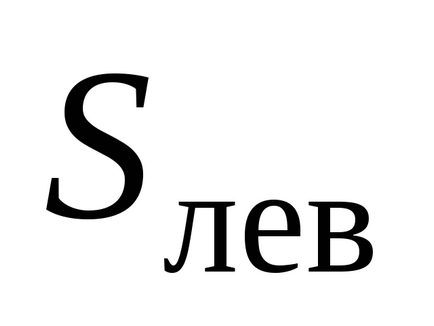
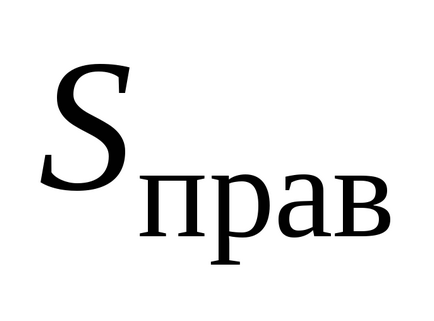
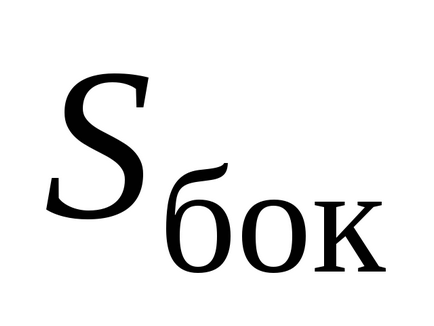
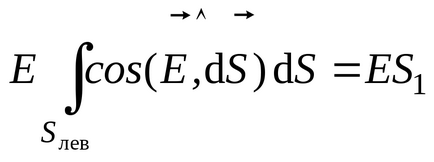
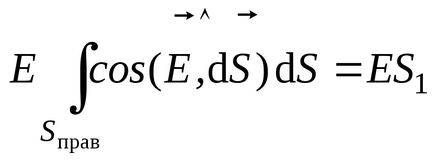
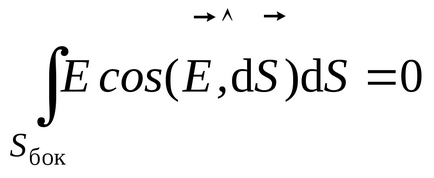
Határozza meg az algebrai összege díjak tartozó Gauss hengerpalást. Ebben az esetben, az elektromos töltés fogott benne - a felelős a „vágott” a lemez henger. Megtalálható megszorozzuk a henger alap területet a felületi töltéssűrűség a lemez:
Egyenlővé (3.8) és (3.9) és az együttható
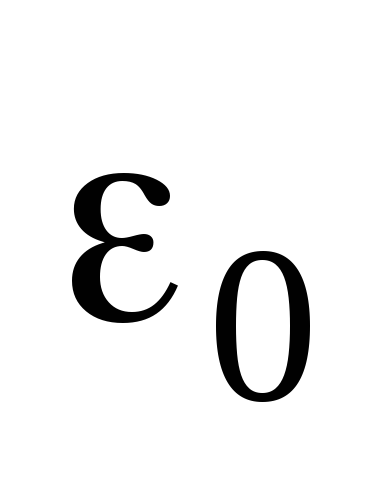
Ez az összefüggés határozza meg a modul egységes térerősség végtelenül nagy töltött lemezeken.
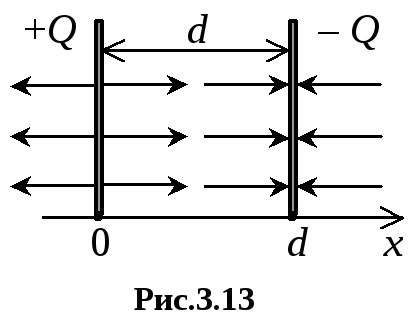
Amikor két ellentétes töltésű lemez elrendezve egy kis távolságra egymástól úgy, hogy kielégítse a feltétele a mező homogenitását (3.13 ábra.), A térerősség lehet figyelembe vételével határoztuk meg szuperpozíció elve (3.10)
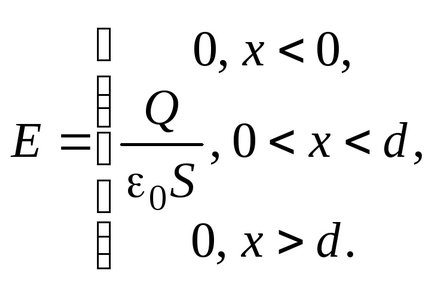
Ebben az esetben, a potenciális különbség az elektródok között a kapott kondenzátor lehet a következőképpen határozzuk meg:
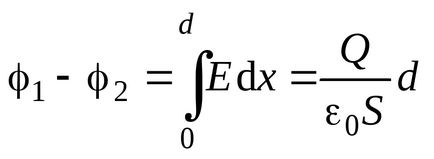
Kapacitás lapos kondenzátor, definíció szerint (3.7), majd
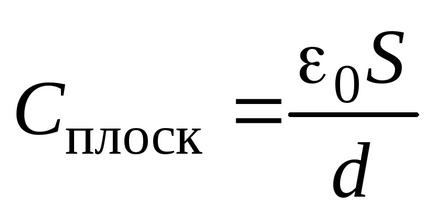
Megjegyezzük, hogy ha a tér között, a lemezek minden egyes kondenzátor töltse dielektrikum relatív dielektromos , majd ugyanazt az értéket a térerősség a töltés elektródok az elektródok közötti csökken alkalommal. Ezért időben csökken a potenciális különbség köztük, és ezért idővel növekedni fog kapacitás:
.
Mi ebből a képlet kapacitív gömbölyű kondenzátorral. Tekintsünk egy rendszer gömb alakú lemezek ábrán látható. 3.9. Tedd a belső bélés Q. töltés és a töltés a külső
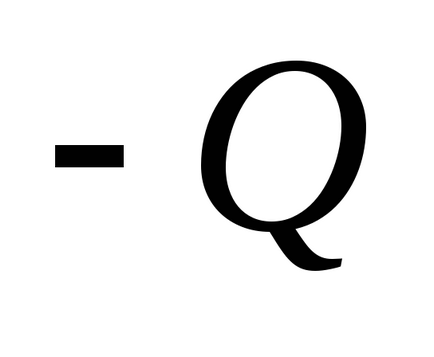
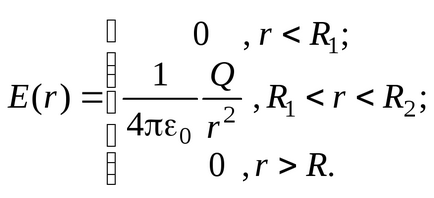
Definiáljuk a potenciális különbség az elektródák közötti, differenciál kötés erőssége, és a potenciál (1,13)
.
Kapacitás Egy gömb alakú kondenzátor, definíció szerint (3.7), majd
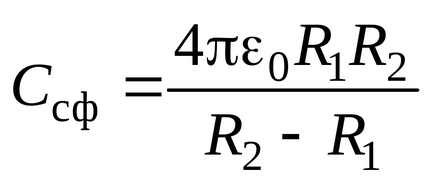
Ha a kondenzátor töltve dielektromos amelynek relatív dielektromos , a
Ismételten hangsúlyozzuk, hogy a kondenzátor kapacitása függ a mérete, alakja és hűtővel relatív dielektromos dielektromos közötti lapok.
11. Az energia az elektromos mező.
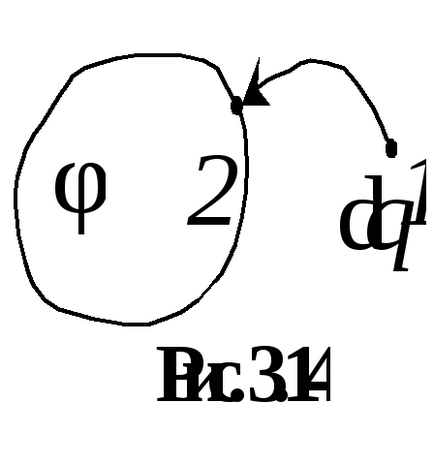
Tekintsük a töltési folyamatban egy magányos felfedező. Ahhoz, hogy elérje a felelős Q. tájékoztatja a vezetőt részeit díj dq. átviszi őket végtelenig a felszínre a vezeték 1 pont 2 (ábra. 3.14). Küldeni egy új díjat vezető részek
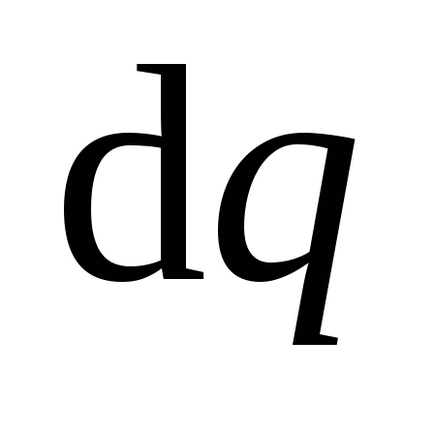
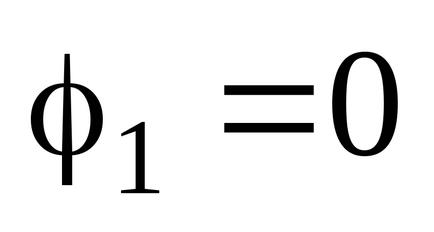
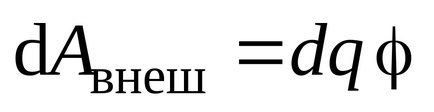
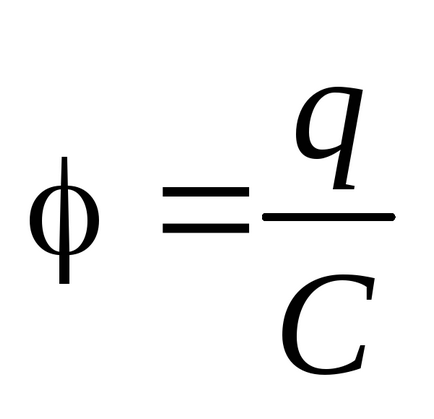
.
A törvény szerint az energiamegmaradás, a munka a külső erők töltés vezeték növeli az energia által az elektrosztatikus tér, azaz a tárolja az egyes energetikai vezető:
Tekintsük a töltési folyamatban a kondenzátort a forrás EMF. Forrás a töltési folyamat a díj átadása az egyik lemezről a másikra, ahol a forrás külső erők erőfeszítéseket tesz az energia a kondenzátor:
,
ahol Q - kondenzátor töltés töltés után. Akkor az energia az elektromos mező által generált kondenzátor definíciója
Egyenlet (3.14) lehetővé teszi, hogy rögzítse a nagysága az elektrosztatikus tér energia kétféleképpen:
Összehasonlítása a két kapcsolat lehetővé teszi, hogy egy kérdést feltenni: mi a hordozó elektromos energia? Díjak (első formula) vagy mező (második képlet)? Mind felvett tőke tökéletes összhangban van a kísérleti eredmények, azaz a mező energia számítás lehet egyformán jól vezet mindkét képlet. Ez azonban csak akkor következik be az elektrosztatika, hogy van, amikor az energia kiszámítását végzik a területen rögzített díjakat. Ha figyelembe vesszük az elmélet az elektromágneses mező a jövőben (Sec. 8) azt látjuk, hogy az elektromos mező lehet létrehozni nem csak fix díjat. Az elektrosztatikus tér - ez egy speciális esete az elektromágneses mező létező helyet olyan elektromágneses hullám. Az energiája eloszlik a tér egy bizonyos sűrűséget. Bemutatjuk a koncepció energiasűrűsége következik.
Transform az utolsó egyenlet (3.14) az esetében a párhuzamos lemezes kondenzátort használva a potenciális különbség, és a kötés erőssége a homogén mező:
,
ahol
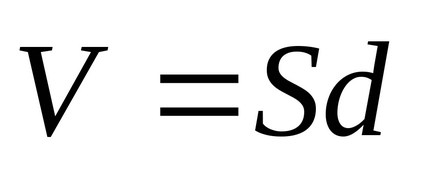
erőtér energiáját térfogatsűrűség aránya az erőtér energiáját zárt kis térfogatú teret, hogy a kötet:
Következésképpen, a homogén elektromos mező az energia lehet a következőképpen számítható ki:
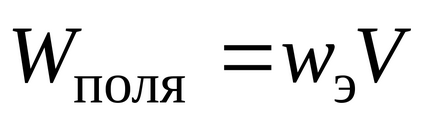
Ezt a következtetést lehet terjeszteni az esetben inhomogén mező az alábbiak szerint:
ahol
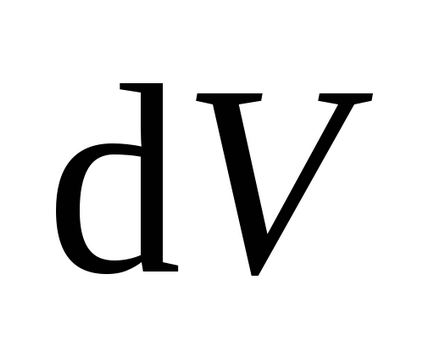
Például számoljuk az energiát az elektromos mező által generált magányos fém golyó R sugarú feltöltött díjat Q. található, és egy olyan környezetben, ahol a relatív dielektromos állandó . Megismételve a érve példa p.2.5 kapjunk egység térerősség függvényében
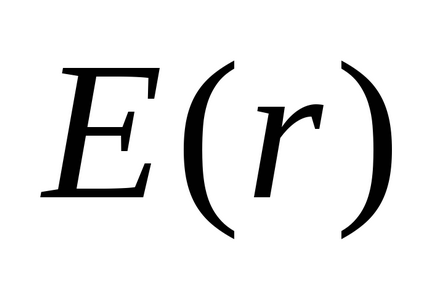
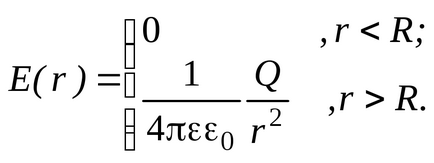
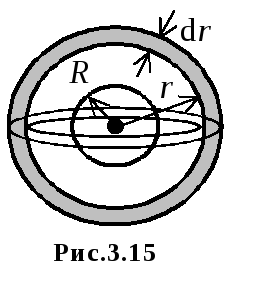
Ezután a kifejezés a térfogati energiasűrűség válik:
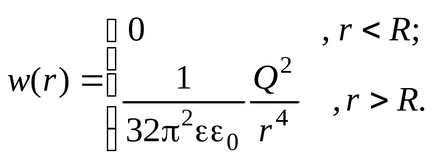
Mivel a térerő csak attól függ, a sugárirányú koordináta, akkor közel állandó belül egy vékony, gömb alakú héj belső sugara r és vastagsága
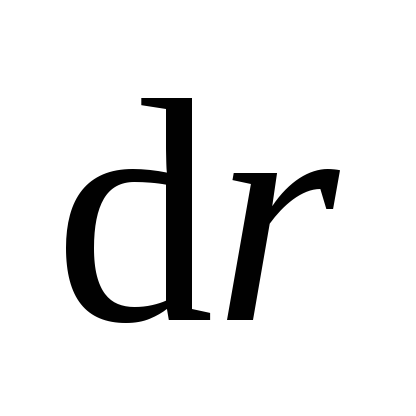
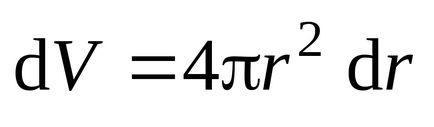
.
Hasonló eredményt kapnánk, ha a számított energiájú töltött gömb, amelyet a képlet (3,13), a (3.6):
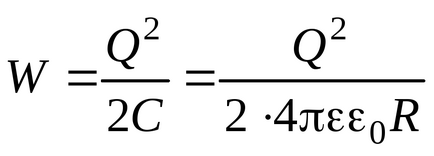
Ugyanakkor tudatában kell lennie, hogy ez a módszer nem alkalmazható, ha kell találni az energia az elektromos mező be van kapcsolva vagy teljes mennyisége a területen, de csak részben. Szintén képlet szerint (3.13), a számítási módszer nem használható annak meghatározására területén energiarendszer, amely nem alkalmazható a „tartály”.