Öt százhúsz rejtvények

373. Négy az érme. Vegyünk 4 azonos érmék és tegyük őket az asztalra segítsége nélkül más érmék vagy más segédanyagokat, így az ötödik érme lehet pontosan illeszkedik a négy adatok mozgatása nélkül az utóbbi (az ábrán satírozott kör képviseli az ötödik érme).

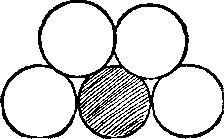
Támaszkodva csak a saját jó szemmel, akkor valószínűleg nem. Ugyanakkor az a feltétel is elvégezhető abszolút pontossággal. De hogyan?

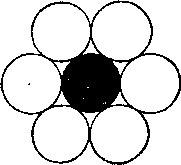
374. Hat érméket. Helyezzük 6. Az érem az asztalra, majd helyezze őket, amint azt az üres körök úgy, hogy a leeresztett hetedik érme (fekete kör) a központban, akkor volna hozta így érintkezik mind a hat érme. Futtatni kívánt biztos, nem „szemmel”. Emel érme az asztalon (különben nem kapott volna semmilyen rejtvények), vagy ilyen méréseket nem engedélyezettek. Az Ön rendelkezésére áll csak hat érme.

Kombinatorikus és topológiai probléma

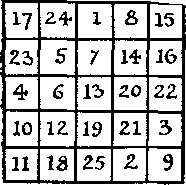
375. Rossz bűvös négyzet. Elhelyezni itt a jobb oldali ábra mutatja bűvös négyzet álló számok 1-16 beleértve. Számok összege minden sorban, minden oszlopban és minden a két nagy átlója egyenlő 34. Most azt feltételezik, hogy nem használhatja a számok a 2. és 15., hanem akkor másolatot kell készítenie a két szám már korábban alkalmazott.

Hogyan gondoskodik a számokat az új tér összessége sorok, oszlopok és átlók egyenlő marad 34? A siker attól függ, hogy milyen számokat cserélni 2 és 15.

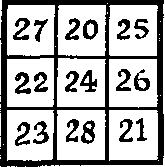
376. A félreértések a bűvös négyzet. Itt van egy bűvös négyzet ötödrendű. Azt találtam, hogy a legtöbb ember nem ismeri az elmélet a mély mágikus négyzetek, és meggyőződése, mintha egy ötödrendű négyzetek közepén száma 13. Egy olvasó szükségszerűen állni évekig szórakoztatta ez a tér, elcsodálkozott, amikor megtudta tőlem hogy a tér közepén bármilyen szám lehet 1-25.

Bizonyítsuk be, hogy ez igaz. Próbáld például, hogy egy mágikus négyzet ötödrendű, amelynek központja az volt, hogy 1.

377. Különbség négyzetek. Tud helyezze a 9 szám egy négyzet, hogy minden sorban, minden oszlopban és minden nagy átlók összege közötti különbség a két szám, a harmadik számjegy egyezik egymással? Ezen az ábrán látható négyzet, amelyben az összes sorokat és az oszlopokat felelnie az előírt feltétel - a különbség bennük 3 (például, 4 + 2 - 3, 1 + június 9-07 + 5 - .. 8, stb), de a átlós „szivattyúzzák fel”, mert a különbség 8 - (4 + 1) és a 6. - (1 + 2) kapott tiltott módon, amely nem az egyik alak le kell vonni az összeget a másik két, és az összeg a két - egy.

Milyen sok megoldás létezik?

378. Nem csinál semmit? Itt van egy egyszerű bűvös négyzet, amelynek összege a számok minden sorban bármely oszlopban a fő átlók egyenlő 72. A puzzle, hogy kapcsolja be a multiplikatív bűvös négyzet, amelynek a terméke számok a bárban, bármely oszlopban, vagy bármely a nagy átlók, volna egymással megegyezik. Nem szabad módosítani a helyek számát, vagy adjunk nekik semmit, és nem is használja a számtani jeleket! Csak akkor lehet mozgatni számokat belül az egyik cellába. Tehát ahelyett, hogy 27 hagyjuk, hogy a 72.

Ha sikerül felvenni a „kulcsot” a megoldás, a probléma az lenne, rendkívül egyszerű. Ellenkező esetben oldja meg a puzzle szinte lehetetlen.

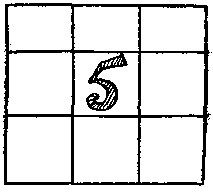
Töltsük terek (lásd. Ábra) számok (minden esetben különböző, úgy, hogy nincs két sejtek nem tartalmaznak ugyanazokat a számokat), hogy a számok összege a lehető nagyobb számú sorok és oszlopok a átló, egyenlő 15. A nyom „kiválasztás „fókusz nevezték ki a fődíjat, de hogy a jobb megoldás nem lehetséges senkinek.

Talán az olvasó, hogy kitaláljuk, mi a baj?

380. A bűvös négyzet négy szám. Mivel ez a tér áll egy és ugyanazon a napon 1234, persze, hogy a számok összege minden sorok, oszlopok és átlók egyenlő. A lényege a puzzle, hogy itt létre és 9 különböző négyjegyű szám (egyféle négyjegyű szám), hogy ők is alkotnak megfelelő mágikus négyzet. Vegye figyelembe, hogy minden számot kell együttesen tartalmazzák kilenc példányban a számjegyek 1, 2, 3, 4, és hogy ez igaznak kell lennie négyjegyű számokat nélkül frakciókat; Nincs semmi trükk itt nem engedélyezett.

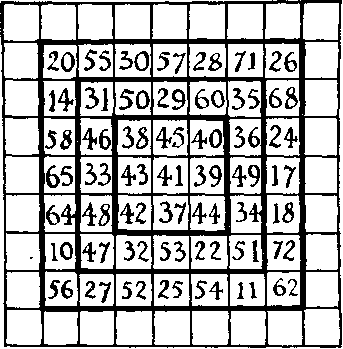
381. Progresszív négyzetek. Itt van egy bűvös négyzet, ami állandó, azaz a számok összege minden sorban, minden oszlopban és a két átló egyenlő: 287. Ha eltávolítjuk a számot szélein helyezkednek el, akkor a másik bűvös négyzet állandó egyenlő 205. Ha ismét távolítsa el a szélsőséges számokat, akkor kap a téren a folyamatos 123. most Töltse fel az üres cellák számát 1-83 befogadó, úgy, hogy a bűvös négyzet állandó 369 annak bármelyik 20 sor.

382. Feltételes bűvös négyzet. Bár viszonylag egyszerű felépítésű mágikus négyzetek semmi hozzá, de maga a tárgy van egy nagyon széles körű, de töredezett, irodalom, apró eltérések néhány új feltételeket mindig okoz érdeklődés. Ez nem egy nehéz egy példa.

Tud építeni egy bűvös négyzet, melynek összege a számok minden sorban, minden oszlopban és a két nagy átló lett volna ugyanaz, a számok 1-25 befogadó, ha elhelyezni a szürke cellákban csak páratlan számok, és mások még? Számos megoldás erre a problémára. Meg tudja találni legalább egyikük?

383. A ötágú csillag. Puzzle with the Stars van egy sajátos vonzereje. Adok egy példát egy puzzle egy egyszerű ötágú csillag.

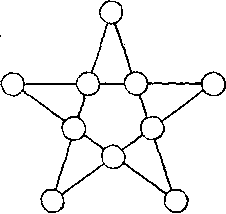
Minden körben ötágú csillag látható itt kell tenni a különböző számokat úgy, hogy az összeg minden négy számot ugyanazon egyenes, egyenlő 24. Solutions tíz egymást követő számok nem léteznek, de használható bármely egész szám, amit akar.

384. A hatágú csillag. Az előző feladat, figyelembe vettük az esetben egy ötágú csillag. Kiderül, hogy a hatágú csillag a helyzet még érdekesebb. Ebben az esetben (lásd. Ábra), akkor mindig a 12 egymást követő számok 1 és 12, és az összeg a négy szám minden sorban mindig egyenlő 26. A számok összege a hat csúcsok bármely szám lehet 24-54 befogadó kivéve a 28. és 50. Ebben a példában ez az összeg megegyezik a 24. Amennyiben helyett az egyes számokat behelyettesítve a különbség közte és a 13, kapsz egy másik megoldást, továbbá ezen, az összeget a csúcsok egyenlő 54 (78 mínusz 24). Két további összegeket összesítve mindig ad 78.