Hogyan állapítható meg, a korrekció a célja az égetés során a cél

A távolság a puskát a cél központ S. Ebben az esetben a cél központ található szintje felett a puskát a összeg h. golyó sebessége V. Ha a cél a fővonalat, a golyó nem érte el a céltábla közepe. Alatt a gravitációs erő, akkor deformálódik, a repülés és elérje a célt közepe alatt. Következésképpen szükség van a cél egy bizonyos képzeletbeli pont fölött a cél központ. Szükség van az eredeti adatokat, általános módon, hogy meghatározza a korrekció a célja, azaz - .. A távolság a látvány pont és a cél központ. légellenállás elhanyagolható.

Nem akarta, hogy megfogalmazzuk a problémát. Először is, a puska nem ez a lényeg. És a távolság „a puska” a végtelenségig. Talán meg kellett többet mondani határozottan, „a távolság a kimeneti végén a puska hordó.” Bár ez a probléma, hogy nem számít, hiszen minden esetben a távolságot le lehet olvasni csak kiömlővégéből a hordó. Hát ez szócséplés. De a következő megjegyzést jelentősebb.

Hagyja, hogy a célkitűzés rögzített függőleges falon. Jelöljük a kimeneti végén a puska hordó pont, és levonjuk belőlük vízszintes, hogy a kereszteződés a fal, amelyen a cél rögzített. Jelöljük ezen a ponton B. A központ a cél e pont fölött, jelöljük pont C. Ezután az A, B és C alkotnak derékszögű háromszög. Az a kérdés, hogy mit értünk a távolság a puskát (a kimeneti végén a hordó), hogy a központ a cél? A távolság AB, ami logikus, ha a feladat, a távolság a cél, vagy ez a távolság AC ( „ez akár a cél center”)?

Egyértelmű, hogy a cél az, hogy egy bizonyos ponton D.

Következő. Mit jelent a „Ha a cél a fővonalat.” Cél nyilak mindig „a fővonalon.” De hol ez a vonal irányul? B pontban (azaz, „fővonalat” azt jelenti, a vízszintes), vagy egy C pont, azaz a a sorban a kimeneti végén a puska hordó a központ a cél? Bár a megoldás ennek a „fővonal”, és nem fogja érinteni, de mégis, arra lenne szükség, hogy egy tiszta készítmény, nem tartozik a különböző értelmezések.

Most, hogy maga a határozat. Vegyük a leglogikusabb lehetőség szerint a távolság S utal, hogy a még mindig távolságot AB. Aztán a nap egyenlő h. Hagyja, hogy a távolság CD (a központ a cél, hogy boresight) egyenlő y. Ezután BD = h + y. jelöli a H távolság egyszerűsítése nyilvántartások, azaz H + y = H. Arra törekszik, hogy a D pontot, akkor a lövedék sebességvektor (V) mentén irányul AD. Felbontjuk azt egy vízszintes (Vx) és függőleges (Vy) komponenseket. Nyilvánvaló, Vx = V * S / √ (S ^ 2 + H ^ 2)

Vy = V * H / √ (S ^ 2 + H ^ 2). golyó repülési idő (t) t = S / Vx = S / (V * S / √ (S ^ 2 + H ^ 2)) = √ (S ^ 2 + H ^ 2) / V.

Mivel a légellenállást elhanyagoljuk, a vízszintes összetevője a sebességet a golyó repülés nem változott, és állandó marad. De a függőleges összetevő (jelöljük a Vv) változik a törvény szerint Vv = Vy-GT, és a golyók magassága (Y), a vízszinteshez képest AB változik a törvény szerint Y = Vy * T-GT ^ 2/2, ahol a g - gyorsulás szabadesés. Természetesen, a végén a lövedék repülési, Y jelentése hidrogénatom. Behelyettesítve t értéke a törvény változása magasság kapjuk:

V * H / √ (S ^ 2 + H ^ 2) * √ (S ^ 2 + H ^ 2) / V-G * (S ^ 2 + H ^ 2) / V ^ 2/2 = h. Miután egyszerűsítés megkapjuk a másodfokú egyenlet vonatkozásában H: H- (g / 2) * (S ^ 2 + H ^ 2) / V ^ 2 = H, amely kényelmesebben képviseli a szabványos formában

Megoldása kapjuk: H = V ^ 2 / g-√ ((V ^ 2 / g) ^ 2-S ^ 2-2 * H * V ^ 2 / g), és végül a korrekció a célzáshoz: y = V ^ 2 / g-√ ((V ^ 2 / g) ^ 2-S ^ 2-2 * H * V ^ 2 / g) -h.

Vasil Stryzhak [6.3K]

Vegyük azt az esetet nem szabványos megoldás.

Az ábra mentett jelölés, a javasolt Rafail.

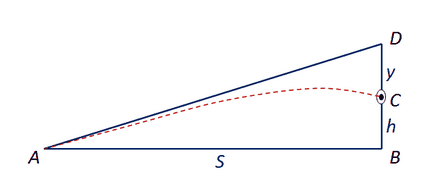
Legyen AB = S távolság a puska egy függőleges fal, amely a cél rögzített. Cél központ található, a fenti B pont értékével órán át a C pontban Másfelől, a szár vonal arra irányul, hogy a D pont, a fenti a központ a cél, hogy a y kívánt értéke szerint. Az eredmény egy derékszögű háromszög által alkotott pont az A, B és D.

Tegyük fel, a golyó nem az erő a Föld gravitációja. Ezután fogja legyőzni a távolságot AD = √ ((S² + (H + U) ²) során t = √ ((S² + (H + U) ²) / V. Képzeljük el, hogy miután üti a falat, hogy a D pontban, golyó kialudt sebesség és már a gravitáció alatt szabadesés elérte a cél központ idején t Ezután a törvény szerint a szabad esés = gt² / 2 behelyettesítve t értéke a variációs magasság ..:

Transform és jelen általános másodfokú egyenlet y:

Megoldására, megkapjuk módosítását célzó: