A megoldás a közlekedési probléma excel
§1. Nyilatkozat a közlekedési problémát (TOR) az n-változós
2. §. Egy példa a megoldás a közlekedési probléma
3. §. Szállítás feladatok különböző szempontok szerint
4.§. A megoldás a közlekedési probléma az Excel
Az úgynevezett „közlekedési probléma” egyesíti a széles körű feladatokat egyetlen matematikai modell segítségével. Klasszikus közlekedési probléma - a probléma a leggazdaságosabb terv szállítás homogén termék vagy helyettesítő termékek pontok termelési fogyasztási helyek előfordul, leggyakrabban a gyakorlati alkalmazás a lineáris programozás. Lineáris programozás egyik ága matematikai programozás - matematika, hogy fejlesszék az elmélet és numerikus módszerek megoldására többdimenziós szélsőérték problémák korlátok.
Rengeteg lehetséges közlekedési lehetőségek megnehezíti, hogy elegendő gazdasági terv empirikus vagy szakértő módon. Matematikai eszköztudás és a számítástechnika, hogy a szállítás tervezés ad egy nagy gazdasági hatása. Közlekedési problémákat meg lehet oldani a szimplex módszer, de a közlekedési problémát megszorítások a rendszer mátrix annyira különleges, hogy különleges módszereket fejlesztették ki azt. Ezek a módszerek, valamint a szimplex módszer, hogy megtalálják kezdeti támogatást oldattal, majd javítása kap az optimális megoldást.
Attól függően, hogy a prezentáció módja a szállítási feladat feltételeit, akkor meg lehet jeleníteni a hálózatban (sematikus), vagy mátrix (táblázatos) formában. A szállítási probléma is megoldható a korlátozásokat és korlátozás nélkül.
§1. Nyilatkozat a szállítási feladatok (TK) dlyanperemennyh
Tegyük fel, hogy van néhány szállítók hasonló termékek (mindegyik egy bizonyos mozgásteret), és néhány e termék felhasználói (az ismert igényeit minden). Szintén adott kommunikációs hálózat (utak, folyók, levegő vezetékek stb) összekötő egyes szállító minden fogyasztó számára. Minden kommunikációs szett ára kocsi - A szállítási költség egységnyi kibocsátás. Ha bármelyik - vagy nincs kommunikáció, akkor azt feltételezzük, hogy az, de a szállítási költség rajta beállított értéke a végtelenbe (+ ∞). Ez a megállapodás teszi veszteségessé szállítás és automatikusan törli ezt a közleményt a szállítási tervet.
Ezért szükséges, hogy a tervet a közlekedési termékek a beszállítóktól a fogyasztókat, hogy a fogyasztók igényeit lehetne kielégíteni eltávolításával készleten a beszállítóktól. A cél -, hogy minimálisra csökkentsék a teljes szállítási költség.
Szállítás problémák:
1) nyitott m ≠ n (a teljes állomány termékek a szállító rendelkezésére álló, nem esik egybe a teljes termék iránti kereslet a fogyasztók körében.)
2) Zárt m = n (összesen készleten a termék beszerezhető a szállítók, egybeesik a teljes termék iránti kereslet a fogyasztók által.)
lehetséges módszer szerint „működik” csak zárt TK, és zárt TK mindig megoldható.
TK csökkentheti a nyitott zárt TK oly módon, hogy a teljes állomány a termékek, illetve a termék teljes igényeinek hiányzó egységek egyenlő a teljes tartalék összegének és a termék gyártási igényeinek.
Zárt közlekedés bonyolult probléma a lineáris programozási feladat (ZLP) a következő:
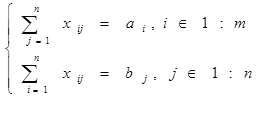
1. Optimalitáselmélet megtört a cella (3,3). Kinevezi a kocsijába # 952;> 0 (+ # 952; átlagos növekedés # 952;).
2.Narushaetsya export egyenlege a kapcsolatot 3 (kivitel 50+ # 952;, amely nagyobb, mint a tartalék!). csökkentsék # 952; szállításra töltött sejtvonal 3 (tele nem lehet csökkenteni, mert ez vezethet negatív kocsi).
Tekintsük azokat a sejtciklus, amely csökkenti a # 952; szállítás és vegye minimum levonni, mi ez min = 10.
És ez a szám a helyébe lép a ciklusban
3. §. Szállítás feladatok különböző szempontok szerint
A közlekedési problémát időben kritérium
Néha olyan helyzet áll elő, ha a körülmények (TK) szükséges, hogy minimalizáljuk a szállítási költséget nem, és a végrehajtásuk idejére (Term terhelés, szállítás a romlandó áruk, a munka a „sürgősségi”, stb)
Ott vagyok a szállítók
egyenletes terhelés és n a fogyasztók
rakomány. Minden egyes pár (
,
, amelyre az árut szállítanak
. Ez szükséges ahhoz, hogy a szállítási tervet, amelyben az összes szállítói állomány törlődik, és minden ügyfél igényeit maximálisan elégedett lesz a szállítási idő és a legnagyobb az összes áru minimális lesz.
Hozzárendelési probléma (Magyar Method)
Vannak n típusú munka és n dolgozók. Minden munkavállaló végezheti el nrabot egy ideje (üzemeltetési költség). Azt akarja, hogy ossza ki a munkát egymás között minden munkavállaló, hogy a szükséges idő minimális volt, de minden munkát végezni csak egy munkás.
4.§. A megoldás a közlekedési probléma vExcel
Példaként azt vizsgálta a közlekedési problémát a 2 tároló és 5 üzletek.
· A sejt-C4: C5 rögzített mennyiségű termék áll rendelkezésre a 2 raktárak.
· Az E5-ös cellát: I5 - Az a kapott termékek a boltokban.
· A B8 cellában: F9 - mátrix szállítási költségek, meghatározva a szállítási költség az I-edik készleten lévő J-edik boltban termelési egység.
· A cella B13: F14 - közlekedési terv - mátrix, a szállított áruk az I-edik készleten lévő J-edik boltban. A kezdeti eloszlása a terv által meghatározott elv „minden ember a fülbevaló testvér”, egyenletesen elosztjuk az összes termék boltban kaphatók raktáron. Ezek a sejtek szabályozott, és a megoldó kell találni egy jobb megoldást értékeinek megváltoztatásával ezekben a sejtekben.
· A sejt D15 - rögzítette a célfüggvény:
· A sejt D17: H17 rögzített korlátozásokat meghatározó követelmény precíz kivitelezés alkalmazásának minden boltban. Szokás szerint írtam le, a megfelelő képletet az első ilyen sejtek:
Majd másolja azt. Formula automatikusan változik másolása közben, amelyben a megfelelő határértéket. Ugyanakkor ügyelni kell arra, ugyanakkor a helyes adatokat orientáció. Például ebben az esetben a képlet kell másolni egy string, és nem egy oszlop.
· Majd megkérdezte a következő megszorítások. Ezek a korlátok megfelelnek a természetes állapot, amely nem veszi el a raktárból több terméket is rendelkezésre áll. Formula helyezzük D18 sejt formájában:
Ez a formula lett másolva egy oszlop cellában D19. Az előkészítő szakasz befejeződött - hívhatjuk a megoldó.
Ha felhívja a Solver és beállítási annak párbeszédablakban végezze alapmű utasításai alapján a sejtet a célfüggvény, a tartományban állítható sejtek és munkahely korlátok. Megjegyzendő, hogy amellett, hogy a két csoport megszorítások és korlátozások tettem egy egész szám. Feltételezzük, hogy a termékeket lehet szállítani csak a teljes egység - dob, zsákok és dobozok. Az ilyen korlátozások Solver meglehetősen egyszerű - csak az üzemeltetők között, amelyek összekötik a bal és jobb oldalán korlátozások válasszuk int operátor. Vegyünk egy pillantást, a megjelenés a munkám eredményei:
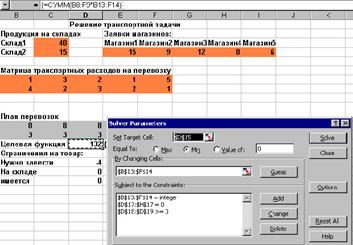
Ábra. 2.21. Ablak Solver megoldására közlekedési probléma
Mielőtt a parancsot, hogy a feladat, töltöttem beállítási lehetőségek a Beállítások. Különösen bekapcsoltam a zászlókat, amelyek jelzik a lineáris modell és a pozitív változás. Ezen kívül, azt növelték a pontosságát az oldat egész szám meghatározott feladatokat a Tolerance értékét 1% helyett 5%, az alapértelmezett.
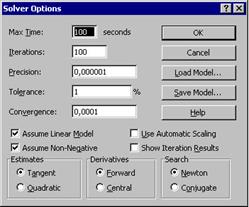
Ábra. 2.22. Beállítása ablak Solver megoldásokat javasol a közlekedési problémát
Bal kattintson a „Problémák” gombra, és az optimális szállítási tervet. Azt is elemezni, hogy az optimális terv eltér egyenletes eloszlását, amint azt az eredeti változat, és hogyan csökkenthető a szállítási költség:
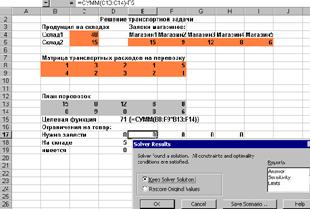
Ábra. 2.23. A megoldás a közlekedési probléma
A vezérlő paramétereket Solver
Tekintsük a teljesítmény menedzsment képességek Solver kérték a Beállítások párbeszédablakban (Opciók):
· A maximális idő (MaxTime) - korlátozza a rendelkezésre álló idő a folyamat megoldásokat találjanak. Az alapértelmezett érték 100 másodperc, ami általában elegendő alkalmazásai kis méretű, mintegy 10 korlátozásokat. A nagy léptékű problémák kell növelni ezt az értéket.
· Maximális iterációk száma (ismétlések) - egy másik módja, hogy korlátozza a keresési idő beállításával a maximális számú ismétléseket. Az alapértelmezett érték 100, de ez a szám növelhető akár 32767 Leggyakrabban ha a megoldás nem kapott 100 ismétléseket, azt reméli, hogy ez mikor növeli ezt az értéket egy kicsit. Sokkal jobb, hogy megpróbálja megváltoztatni a kezdeti közelítés és a keresés elindításához folyamatot.
· A relatív hiba (Precision) - meghatározza a pontosságát teljesítőképesség határait. Néha könnyebb megváltoztatni a limit, nyomja a határ, mint hogy megpróbálja végrehajtani korlátozásokat pontosan.
· Konvergencia (konvergencia) - adják tizedes tört, kevesebb, mint egység, amely lehetővé teszi, hogy hagyja abba a keresést, ha megoldásokat konvergencia a fix pont, amikor a relatív változás az elmúlt 5 ismétléseket nem haladja meg az előre meghatározott frakciót.
· A lineáris modell (Tegyük fel, Linear Model) - ez az opció is, amikor a célfüggvény és korlátok - egyenest. Ez a kiegészítő információ lehetővé teszi, hogy a megoldó, hogy egyszerűsítse a folyamat megoldásokat találjanak.
· Nem negatív értékek (Tegyük fel, nem-negatív) - ez a zászló, akkor meg korlátozásokat a változókat, amelyek megoldást keresnek a pozitív tartományban az értékek megadása nélkül a különleges korlátozások az alsó határ.
· A kijelző iterációt (Show Iteration Eredmények) - ellenőrizze, amely lehetővé teszi, hogy tartalmazza a folyamatot lépésről lépésre a megállapítás, rámutatva, hogy a képernyő minden egyes iteráció. A nehéz helyzetekben, amikor a Solver megállapítja megoldások automatikusan, akkor ajánlott, hogy ezt a lehetőséget, mert akkor néha megtalálni azt a pontot, ahonnan a keresési folyamat kitért az oldalon.
· Automatikus méretezés (Use automatizálása skálázás) - automata zoom box kell vonni, ha a skála értékeit a bemeneti változók és a célfüggvény és korlátok különböznek talán nagyságrenddel. Például változókat beállítottuk a darab, és az objektív függvény meghatározza a teljes költség, mért millió rubel.
· A relatív hiba (tolerancia) - százalékban adjuk. A megadott érték csak akkor van értelme a problémák egész korlátok. Megoldó ilyen problémák az első talál az optimális megoldás nem egész, majd megpróbálja megtalálni a legközelebbi egész pont olyan határozatot, amely eltér az optimális legfeljebb egy meghatározott mennyiségű érdeklődés ezt a paramétert. Ha egy ilyen pont is található, a megoldó jelentések siker. A nagy tolerancia (alapértelmezett 5%) elveszítheti a legjobb egész megoldás azonban eltér a megtalált megoldó tűréshatáron belül. Integer problémák tolerancia értelme csökkenteni, amit meg is tettem megoldásában a közlekedési problémát. Szeretném ismételten felhívni a figyelmet a funkció megoldására egész programozási feladatok. Ha az érték a tolerancia paraméter készlet nagy, a megoldó elromlik az idő, nem kap a legjobb egész megoldás. Ha elvisszük alacsony, a legjobb egész megoldás eltér a noninteger optimális megoldást nagyobb mennyiségben, mint amit megadott paraméter tolerancia. Ebben az esetben a hivatalos döntést, hogy véget a sikertelenség, mert a talált megoldás nem felel meg az előírt követelményeknek. Természetesen tolerancia paraméter játszik kisegítő szerepet, és az „intelligens” Solver megtalálni a legjobb egész megoldás az lenne, hogy tájékoztassuk megoldás, hanem a tolerancia határa nem teljesül. Ez azonban nem fordul elő. Még mindig szembe ezzel a helyzettel, ha figyelembe vesszük a következő probléma.
· Save modell (Save Model) - egy nyomógombbal; Ez lehetővé teszi, hogy egy párbeszédpanel, ahol megadhatja a nevét a tárolt modell szerint. Logikus, hogy használja ezt a beállítást, ha a munkalap több modell, mert ez az egyetlen modell automatikusan tárolja.
· Letöltés Modell (Load Model) - lehetővé teszi, hogy töltse be az egyik tárolt mintákat.
· Van néhány konkrétabb paramétereket, amelyek változtatásával szabályozható az alkalmazott eljárások a keresési folyamat. Ezeket kell használni, súlyos esetben, ha a döntés nem található.