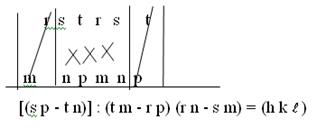Meghatározása az arcok karakterekből élek és egyszerű formák - studopediya
karakterek arcok alapján határozzuk meg az építőiparban a sztereografikus vetülete a kristály. Karakterek arcát - egy matematikai kifejezést arcokat, amellyel lehet, hogy bizonyos matematikai műveleteket. A törvény alapján az RJ Hauy karakter arcok kerülnek meghatározásra. Kettős kapcsolat paramétereit, levágta a két oldalát a kristály az ő három egymást metsző bordái közé egymás között, mint a kis- és egészek. Három borda - ez koordinátatengelyt által kiválasztott sorok rács. Az egyik felület van kiválasztva, mint a skála, szimbólumok bármely más arc képest van meghatározva, hogy a skála. Scale vagy egység arc kiválaszthatja a legelőnyösebb módon, de a kívánt arc lehet párhuzamos egy vagy két tengely, majd levágta az arány a paraméterek lesznek:
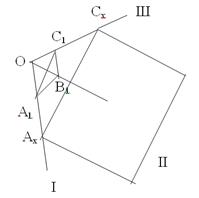
A második kifejezés ez a kapcsolat - a bizonytalanság - kínos számát. Ezért Miller arra kérték, hogy fordított összefüggés - a - minden ravnootnositelnye.
Írunk ez az egyenlet másik formában:
Egész kapcsolat a végtelenig úgy definiáljuk, mint nulla, ami azt jelzi, hogy a kívánt arc párhuzamos a második tengellyel. Kívánt arc párhuzamos a harmadik tengely, a szimbólum lesz formájában (h. K. 0), párhuzamosan a két tengely (h. 0. 0). A forma változó: a szögek között az arcok, hogy nem mérik és még nem lehet kiszámítani, jelöljük leveleket. Rendszeres formák: a szögek felületei közötti állandó szimbólumok a következők: a vonal hexaédernek -, a vonal rombododekaéder -, az arc egy köbös tetraéder -.
A változó formái: rombusz prizma -, rombusz piramis -, rombusz tetraéder -. Szimbólumok élek, ellentétben szimbólumok arcok által meghatározott közvetlen kapcsolatokat. Például, a szimbólum az első koordináta tengelyt és a bordák tengellyel párhuzamos, definíció szerint a [1 0 0]. Symbol bordák, síkjában fekvő első és második tengely, de merőlegesek a harmadik, - [1 1 0]. Symbol átlója a kocka, akkor definíció szerintSzimbólumok bordák szögletes zárójelek között, ellentétben az arcok karakterek mindig jelöljük, zárójelben.
A szimbólumok egyszerű formák általános szimbólumok minden arcok ezek a formák. Például: karakter arcok hexaédernek, specifikus elhelyezve képest a koordináta tengelyek jelöljük (1 0 0), (0 1 0), (0 0 1), (0, 0), (0, 0), (0, 0) .
Mind a hat oldalán át a pozitív és negatív végei tengelyek és különböző karaktereket.
Symbol egyszerű kocka alakú tükröznie kell a jellemző ebben a formában, és annyi karaktert, hogy a pozitív oldalát, és tegye zárójelek azt mondani, hogy ez egy általános szimbólum kocka -. Szeretné tudni, hogy az adott helyzetben a arcok kapcsolatban koordinátatengelyeken, látni az arcokat a karakterek zárójelben, ahol a meghatározott hely egységekben, ahol jelölt negatív és pozitív kereszteződésekben a tengelyek.
Ha a koszinusz tétel G.V.Vulfa tervezett karakterek arcát, akkor lehetséges a segítségével bizonyos módszerekkel meghatározható a karakterek más arcok és élek.
Goldschmidt törvény alapján jelenlétében a két oldalát a karakterek, akkor létrehozhatunk egy szimbólum harmadik arc, eltompítja a szélén az arcok, amelyek ugyanabban a zónában.
Symbol egy arc, a törvény Goldschmidt -
np (1 0 2) úgy definiáljuk, mint az algebrai összege:
r s t h k + r s t + (3 0)
(3 0) hk (április 2)
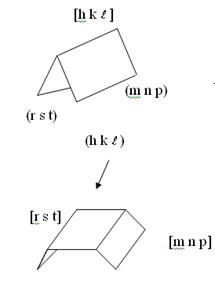
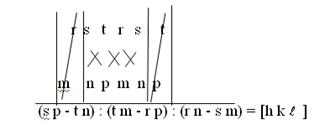
Ez a módszer alkalmazható a fordított kiviteli alakban:
Köztudott két bordáját, és azok értékét is
meghatározzák a karakter arcát, csatolva a