A többdimenziós rendszer - studopediya
Többdimenziós vagy többszörösen - a rendszer több vezérelt változók, valamint számos meghatározó és zavarok. Többdimenziós rendszer meglétét feltételezi többdimenziós objektumok (4.6 ábra), amelyet az jellemez, fennállásának több bemenet (pont alkalmazásának ellenőrzése és zavarok) és többszörös kimenet, amelyet a manipulált változó.
Ábra 4.6. Többváltozós vezérlő objektum
Többdimenziós objektum által leírt egy egyenletrendszer, amely kényelmesen képviseli mátrix formában. Ebben az esetben, a koordinátáit a vektor kontroll rendszer a referencia változó G (t), a szabályozott mennyiségű vektort Y (t), a kontroll vektorral U (t), és a vektor az F (t) zavar. Ebben az esetben,
Működési séma egy többdimenziós rendszer formájában ábrán látható 4.7.
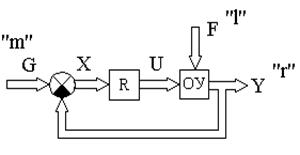
Ábra. 4.7. Működési séma egy többdimenziós rendszer
A blokkvázlat ábrán látható 4.8.
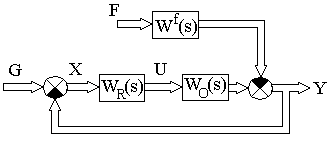
Ábra. 4.8. A tömbvázlata többdimenziós rendszer
Ott WR (s), W0 (s), W f (s) - átviteli függvény mátrix vezérlő és a rendszer kezelése objektumot.
Mátrix többváltozós lineáris differenciálegyenlet rendszer permited vonatkozó ellenőrzött mennyiségének a formája:
D (p) Y (t) = R (p) G (t) - N (p) F (t), (4.9)
-
négyzetes mátrix együtthatók (dimenzionalitás R'R, ahol r - számú ellenőrzött változók), amely jellemzi a viselkedését a rendszer szabad;
-
egy derékszögű mátrix együtthatók (dimenzionalitás r'm, ahol m - számot, amely megad akciók) összekötő referencia változó a szabályozott jellemző;
-
egy derékszögű mátrix együtthatók (dimenzionalitás r'l ahol l -. száma zavarok) összekötő zavart a szabályozott érték.
Alávetése az egyenlet (4.9) van a Laplace-transzformáció, megkapjuk a mátrix üzemeltető egyenlet, amelynek megoldása határozza meg a szabályozott mennyiségű képet
-
mátrixa átviteli függvények zárt rendszer;
-
mátrixa átviteli függvények a zavaró hatások a zárt rendszer.
Ott FIJ (ek) - átviteli függvénye a zárt hurkú rendszer összekötő i-edik kimenetre a j-ötödik input rendszer.
Hasonló módon állítjuk elő Noe mátrix differenciálegyenlet megoldotta a hibát, és a hiba képet meghatározzuk.
KÉRDÉSEK 4. szakasz
1. Hogyan szerezhető matematikai leírása egy zárt rendszer?
2. írása általában kezdeti differenciálegyenlet zárt hurkú szabályozó rendszer.
3. Mi a karakterisztikus polinomja a rendszer?
4. Sorolja az átviteli függvény a zárt rendszer.
5. Mi az átviteli függvény a nyílt hurkú rendszer?
6. Adjon az átviteli függvény a zárt rendszer a nyitott hurok átviteli függvény.
7. Hogyan határozza meg a karakterisztikus polinomja az átviteli függvény a nyílt hurkú rendszer?
8. Adja meg a meghatározását többdimenziós rendszer és többdimenziós ellenőrzési objektumot.