Szabad tartós oszcillációk oszcilláló áramkör
Szabad tartós oszcillációk oszcilláló áramkör.
Rezgéskör - egy elektromos áramkör, amely sorba kapcsolt tekercs L induktivitást, C kondenzátort és egy ellenállást R.
Tekintsük a következő egymás utáni lépéseket oszcilláció folyamat ideális áramköri elhanyagolható ellenállást (R = 0).
A kondenzátor előzőleg bevisszük, a töltés a lemezeken. Ezután, a kezdeti időben a lemezek között egy elektromos teret, amelynek energiája. Ha a kondenzátor közel a tekercset, akkor elkezdi kirakni és folyna az áramkörben áram időben nő az I. elektromos mező energiája a kondenzátor csökken, és a mágneses mező energiája a tekercs növekszik. Időben növekszik a tekercs áram termel növekvő mágneses mező, és, következésképpen, növekszik a mágneses fluxus. Szerint ezért Faraday indukciós törvénye, indukciós előfordul a tekercs áram, amely felé a kisülési áram a kondenzátor és a növekedést lassítja azt. Mivel R = 0. a törvény szerint az energiamegmaradás az összes energia a rendszer állandó marad, mivel A fűtési energia nem fogy:
Amikor tekercs áram maximális értéke, a kondenzátor teljesen lemerült. Ezen a ponton, a mágneses mező energia legnagyobb és a legkisebb elektromos mező. Továbbá, elérve a maximális értéket, a jelenlegi az áramkörben csökkenni kezd, így csökken a mágneses mező tekercset. Ez felmerül egy indukciós áram, amely folyik a iránya megegyezik a kisülési áram a kondenzátor. A kondenzátor feltöltődött, a töltés a lemezeket eléri a maximális értéket, és az áram a tekercs nulla. Az energia az elektromos mező elér egy maximális és egy minimális mágneses mező energiát. Ezután folyamatok fordulnak elő az ellenkező irányba.
Szerint Ohm-törvény - EMF induktivitás tekercs, - a kondenzátor feszültsége, - definíció szerint.
Aztán. A megoldás ennek az egyenletnek, így töltés változik harmonikusan a gyűrűs frekvencia és az idő - Thomson képlet.
A kondenzátor feszültsége:
, ahol - a legnagyobb érték a kondenzátor feszültsége.
Az áram a rezgőkör:
azaz aktuális szinuszosan változik, és megelőzve a oszcillálás fázis kondenzátor feszültsége a / 2. Ez azt jelenti, hogy ha a jelenlegi eléri a maximális értéket, a töltés és a kondenzátor feszültsége nulla, és fordítva.
Szabad csillapodó rezgések oszcillátor áramkört.
Minden igazi rezgőkör egy aktív ellenállás. A tárolt energia hurok fokozatosan fogy a fűtés, ami miatt a szabad rezgések és csillapított.
Ohm törvénye rezisztencia oszcillátor áramkör:
, - EMF induktivitás tekercs, - a kondenzátor feszültsége, - definíció szerint.
Jelöljük. Ezután a differenciálegyenlet írható fel.
Feltéve, hogy a megoldás ennek az egyenletnek a kifejezés, azaz a költség-ingadozás frekvencia.
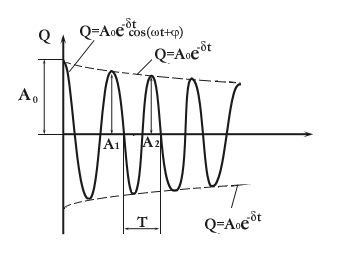
A kondenzátor feszültsége:
Azóta. Így, ha az áramkör ellenállását áramerősség vezet fázisban a kondenzátor feszültsége több mint / 2.
Logaritmikus csökkentő :.
Annak érdekében, hogy kompenzálja a tényleges vibrációs rendszer energiaveszteség és kap tartós rezgések kell dolgozni egy rendszert külső hajtóerő, amely időben változik szerint a harmonikus törvény.
Abban az esetben, a rezgőkör szerepet tölt be a hajtóerő a jelenlegi forrás EMF . Szerint Ohm-törvény:
Megoldás az inhomogén differenciálegyenlet:
Az általános megoldás a homogén differenciálegyenlet:
. Miután elég hosszú ideig faktor kevés lesz, és el lehet hanyagolni. Ez a határozat csak akkor játszik szerepet létrehozó oszcilláció.
Egy különösen oldatot az inhomogén differenciálegyenlet:
Steady-indukált oszcilláció határozza meg a kifejezést.
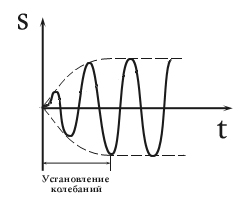
Az áram az :. Írunk a kifejezés formájában: ahol - fáziseltolódás a jelenlegi és az alkalmazott feszültség. majd
Következésképpen a jelenlegi elmarad a prilozhennogonapryazheniya ha és amikor a feszültség előre.
A feszültség az aktív ellenállás :.
A kondenzátor feszültsége: hol
A feszültség a tekercs:
Így, a feszültség a tartály mögött a jelenlegi erőssége a fázisban / 2. A feszültség a tekercs vezeti az áramot / 2. A feszültség az ellenállás fázisban van a jelenlegi.
Harmonikus rezgések állítható be a vektorba. Vegyünk például egy egyenes vonal, amely a számított kezdeti szakaszában áramok tengelyen. Aztán a feszültség az ellenálláson, a kondenzátor és a tekercs is képviselteti magát a diagram. A teljes feszültség egyenlő kell legyen a feszültség, mint szerint Ohm-törvény. Ezért, az ábrán U feszültség képviseli, az összegével egyenlő a vektorok.
A képlet az következik, hogy az amplitúdó a töltés és kondenzátor feszültsége van egy maximális frekvencián wrez. Ahhoz, hogy megtalálja a szükséges legnagyobb mérték különbséget a kifejezést az amplitúdó frekvencia, megkapjuk. Amikor a rezonancia görbék egy ponton.
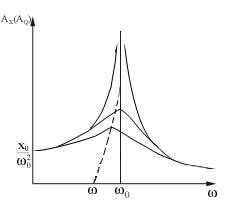
Az áram amplitúdója van a rezonáns értéket. Ezért a rezonancia frekvencia az aktuális egybeesik a természetes frekvencia az áramkör. A rezonancia görbe az I áram nulláról indul, mert állandó feszültség állandósult áramkör egy kondenzátor nem tud folyni.
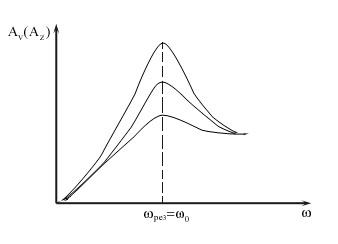
Maxwell-egyenletek az következik, hogy a váltakozó mágneses tér generál váltakozó elektromos tér és a váltakozó elektromos mező generál váltakozó mágneses mezőt. Ie elektromos és mágneses mezők elválaszthatatlanul kapcsolódnak egymáshoz. Alkotnak koherens elektromágneses mező. Ha kezdeményezni oszcilláló keresztül töltődnek váltakozó elektromágneses mezőt a környező tér keletkezik sorrendben egymásba az elektromos és mágneses mezők terjedő térben pontról pontra. Ez a folyamat az időszakos időben és térben, és egy elektromágneses hullám.
Megmutatjuk, hogy a elektromágneses hullámok létezését származó Maxwell-egyenletek:
Abban az esetben, egységes semleges ( = 0), nem vezetővé (j = 0) egy közepes állandó és Maxwell egyenlet átírható:
Vegyük a göndör egyenlet mindkét oldalát (1):
arányt tekintjük, hogy az itt használt. Szerint (3) az első ciklus a expresszió (5) nulla. Ezért.
Sorrendjének megváltoztatása differenciálódás tekintetében koordinálja és időt eredményez a következő egyenletet:
A (2) összefüggés megkapjuk
Hasonlóképpen, tudjuk szerezni egyenletet a vektort N azáltal, hogy a göndör a (2) egyenletnek:
Egyenletek (6) és (7) elválaszthatatlanul össze vannak kapcsolva egymással, például nyerik azokat Maxwell egyenletek, amelyek tartalmazzák mind az E és H.
Egyenletek - képviselnek hullámegyenlet, a fázis sebessége a hullám. Bepároljuk. Egy olyan környezetben. Ie c - sebességét elektromágneses hullámok terjedését vákuumban - egy határ sebessége elektromágneses hullámok terjedését.
Tekintsünk egy sík elektromágneses hullám terjesztő homogén semleges ( = 0). nem vezetővé (j = 0) környezetben állandó és . Mi irányítja a X-tengelye merőleges a hullám felülete, azaz, vektorok E és H és azok összetevői mentén a koordináta-tengelyek nem függenek koordinátákat y és z.
Akkor Maxwell egyenletek írhatók, mint:
Ily módon, és nem függnek az x.
Írunk az x-edik komponens rotorok E és H:
Így, nem függ az x és t. azaz hullám mezőnek nincs komponenseket az x tengely mentén. és ezért a vektorok E és H irányára merőleges hullámterjedés. Ez azt jelenti, hogy az elektromágneses hullámok keresztirányú.
Tegyük fel, hogy eredetileg létrehozott mezőben tengelyének irányába y. Szerint a Maxwell-egyenletek, ezen a területen létrehoz egy váltakozó mágneses mezőt irányítani a Z tengely mentén. Egy másik változat szerint Maxwell egyenletek, ezen a területen egy elektromos erőteret. Tehát a vektor E és H merőlegesek
Differenciálás az első egyenletben x. és behelyettesítve a második egyenletbe, megkapjuk és.
A megoldás, hogy az egyenletek a funkciók:
, ahol k - hullámszám, 1 és 2 - kezdeti fázisban.
Behelyettesítve ezeket a kifejezéseket a egyenletek és. kapjuk:
Annak érdekében, hogy megfelelnek a szükséges egyenletek a kezdeti fázisban egyenlőek: 1 = 2. E kettő szorzatával egyenletek. Így a rezgések a vektorok E és H vektorok fordul elő fázis és amplitúdó minden időpontban kapcsolja össze :.
Tulajdonságok elektromágneses hullámok:
1. A Maxwell egyenletek az következik, hogy a feszültség vektorok E és H az elektromágneses mezők megfelelnek a hullám egyenlet:
, ahol - Laplace operátor, v - a fázissebesség.
2. A fázissebesség adja meg: ahol a és o o - elektromos és mágneses állandók, és - elektromos és mágneses permeabilitása a közeg. Vákuumban bepároljuk, és a sebesség az elektromágneses hullámok terjedésének egybeesik c sebességgel. mert , A sebessége az elektromágneses hullámok terjedésének az anyag mindig kisebb, mint a terjedési sebessége elektromágneses hullámok vákuumban.
3.Elektromagnitnye keresztirányú hullám, azaz és a vektor az elektromos E és mágneses H mezők kölcsönösen merőleges hullám, és egy síkban fekszenek merőleges vektor v sebességének terjedését.
4. A vektorok E és H mindig ingadozhat azonos fázisban, pillanatnyi értékek az E és H bármely ponton kapcsolódnak a
5. hullámegyenlet kielégítik a lapos monokromatikus hullám (szigorúan meghatározott hullám frekvenciájának):
, ahol k - hullám számot.
Az energia az elektromágneses hullámok. Poynting vektor. az elektromágneses tér impulzus.
A térfogati energiasűrűséget az elektromágneses hullám áll ömlesztett sűrűségű és wel WM elektromos és mágneses mezők:
Az energia sűrűsége az elektromos és mágneses mezők minden egyes időpontban azonos.
Ha az energia sűrűsége szorozva a terjedési sebessége hullámok a közegben, kapunk egy modult a teljesítménysűrűség S = hv = EH. mert vektorok E és H merőlegesek, az irányt a vektor egybeesik az irányba energia transzfer. Vektor elektromágneses energia fluxus nevezett Poynting vektor: Ez felé irányul az elektromágneses hullám.
Felszívódik bármilyen szerv, elektromágneses hullám szerint ez a testület néhány momentum, azaz a Ez nyomást gyakorol rá. Lebegyev kísérletek 1908-ban, amely igazolja, hogy a fény a test nyomás.
Legyen egy sík elektromágneses hullám incidens a sík felületre a gyengén vezető testület. Az elektromos mező az elektromágneses hullám gerjeszti a test áramsűrűség. A mágneses mező hat egy aktuális hullám Amper erő, amely egységnyi térfogatú test egyenlő :. Következésképpen, a felületi réteg egységnyi területen és vastagságú dl. számolt impulzus :. Ugyanabban a rétegben az elnyelt energia egységnyi idő. Osztjuk egymással ezeket a kifejezéseket. ()
Következésképpen, az elektromágneses mező impulzus egységnyi térfogatra :. Poynting vektor. Irányvektorok P és S egybeesik.
Scale az elektromágneses hullámok.
Az elektromágneses hullámok span széles frekvenciatartományban. Azonban különböznek egymástól, ahogy a termelés és a regisztrációs eljárás, valamint azok tulajdonságait. Ezért, az elektromágneses hullámok vannak osztva típusok: rádióhullámok, fényhullámok, X-sugarak és a - sugárzás. (Lásd 5. táblázat a következő oldalon 298 Mills T. Kus fizika).
Legfontosabb meghatározások és törvényei geometriai optika.
Fény elektromágneses hullám. Az elektromágneses hullám rezgésbe vektorok E és H. Mint a tapasztalat azt mutatja, egy másik hatása a fény anyag pontosan rezgések az elektromos vektor. Ezért, az elektromos mező vektort az elektromágneses hullám az úgynevezett könnyű vektort. fény vektor képviseli az amplitúdó modul A.
Abszolút törésmutatója a közeg egy mennyiség arány egyenlő a sebesség az elektromágneses hullámok vákuumban való fázissebesség közegben.
A vonal mentén, amely a fényenergiát, az úgynevezett sugarak. A modul időben átlagolt energiát fluxus által hordozott fényhullám nevezik I intenzitását a fény egy adott pontban. Következésképpen ,. . Következésképpen ,. Akkor írtam.
A pontszerű fényforrás - forrás nagysága ami elhanyagolható képest a megvilágított tárgy vagy egy távolságban is.
A törvény egyenes vonalú fény terjedését. fény optikailag homogén közegben (közegben egy konstans törésmutatójú) kiterjed egy egyenes vonal. Ennek bizonyítéka a jelenléte az árnyék a törvény egyértelmű határvonal -megvilágítás átlátszatlan tárgy. A törvény összetörik, ha a fény áthalad a kis lyukak.
Act of Independence fénysugarak. a hatást az egyes gerenda nem függ attól, hogy vannak más gerendák vagy egyidejűleg nem.
Amikor a fény esik a határ két média, a beeső fénysugár két részre van osztva - a reflexió és fénytörés.
A törvény az elmélkedés. A beeső fénysugár, a visszavert nyaláb és merőleges a csökkentett felület két média a beesési pontjától egy síkban fekszik, és a beesési szög egyenlő a visszaverődési szög a.
A fénytörési törvény. A beeső fény, a gerenda megtörik, és merőleges a csökkentett felület két média a beesési pontjától egy síkban fekszik. Sine a beesési szög utal, hogy a szinusz a szög fénytörés, mint a törésmutatója a második közeg a törésmutatója az első közeg :.
Ha a fény egy optikailag kevésbé sűrű közegben az optikailag sűrűbb, azaz n1
Növelésével a beesési szög és a szög fénytörés megnő. Egy bizonyos beesési szög o. szög fénytörés 2 = 90 O. A további növekedés a beesési szög, nincs megtört fénysugár, és a fény teljesen visszaverődik a felületen két média. Ahogy közeledünk a beesési szög, hogy korlátozza az intenzitás a megtört fénysugár csökken, és tükröződik növekszik. Amikor i = ipred intenzitása megtört fénysugár nulla, és a visszavert - intenzitással egyenlő a beeső. Ezt a jelenséget nevezik a jelenséget teljes visszaverődés.
teljes visszaverődés jelensége használják teljes visszaverődés prizmák. üveg törésmutatója n = 1,5, így ipred = 42 0 (arcsin 1 / 1,5). Amikor fény esik a határ a pohár - a levegőben, amikor i> ipred. akkor teljes mértékben tükrözi. Beam lehet forgatni 90 0. sugarak csomagolja, forgassa el a képet.
teljes visszaverődés a jelenséget használják rostok, amely egy fényvezető magüveget köpeny vesz körül egy másik üveg egy kisebb törésmutatójú. Beeső fényt a homlok- szögben nagyobb korlátot a határa a mag és a héj részén megy keresztül teljes visszaverődés és terjed csak fénylő mag.
Vörösvértest és a hullám elmélet a fény.
Az alapvető törvényei geometriai optika óta ismert az ókori görögök. Néhány gondolat a fény természetéről transzformált 17-19 században. A végén a 17. században két elmélet a fény: korpuszkuláris (Newton) és a hullám (Hooke és Huygens). Korpuszkuláris elmélet leírja a kölcsönhatás a fény és az anyag kérdéseket (szórás, abszorpció), és a hullám elmélet a fény terjedési is jól leírták törvények (diffrakció, interferencia). Az egyik elmélet, hogy teljes mértékben leírja az összes törvényei sugárzás terjedését és felszívódását fény nem. Figyelembe véve a nyilvánvaló hullám-részecske kettősség.