Az egyenlet a Nernst-Plank
A transzfer molekulák (vagy atomok) a membránon keresztül. Fick egyenlet
Fontos elem a működése membránok képesek átadni, vagy sem, hogy adja át a molekulák (atomok) és ionokat. Lényeges, hogy a valószínűsége a penetráció a részecskék függ irányokat azok mozgását, például egy sejt vagy a sejt, és a különféle molekulák és ionok.
Ezeket a kérdéseket tárgyalja részben a fizika a szállítási jelenségek. Így a kifejezés a visszafordíthatatlan folyamatokat, így a fizikai rendszerben történik térbeli mozgása (transzfer) A tömeg, lendület, energia, erő, vagy bármely más fizikai mennyiség.
Átviteléhez jelenségek közé tartoznak diffúzió (anyagszállítás anyag), a viszkozitás (momentum transzfer), hővezető (energia transzfer), elektromos vezetőképesség (elektromos töltés átviteli). Itt és a következő bekezdésekben tartják a legfontosabb a biológiai membránok jelenség: az átutalás az anyag és díj átadása. Szinonimaként részecske közlekedés biofizika is kapott nagy távon részecske közlekedés.
Levezetjük az alap diffúziós egyenlet (Fick egyenlet), figyelembe véve az átviteli folyamat folyadékokban.
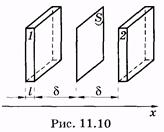
Áteresztő egy bizonyos területen S (ábra. 11.10) minden irányban mozgó folyékony molekulákat. Mivel az elmélet a molekuláris szerkezete folyadékok (lásd. § 7.6), azt mondhatjuk, hogy a molekulák át a platform, ugrás egyik egyensúlyi helyzetből a másikba.
A távolságok d megegyezik az átlagos mozgását a molekulák (az átlagos távolság a molekulák közötti a folyadék), a jobb és a bal pad megépíteni a paralelepipedonja kis vastagságú l (l < Minden molekulák miatt kaotikus mozgás lehet hagyományosan képviseli hat csoport, amelyek mindegyike mentén mozog, vagy ellentétes irányban az egyik koordináta-tengely. Ebből következik, hogy a merőleges irányban a földre S, mentén OX tengelye az első paralelepipedon ugrik 1 / 6Slnl molekulák, és szemben a második tengely OX paralelepipedon ugrik l / 6 Sln2 molekulák. idő Dt<«пролета» этими молекулами площадки S может быть найдено следующим образом. Предположим, что все молекулы из выделенных объемов движутся с одинаковыми средними скоростями . Тогда молекулы в объеме 1 или 2, дошедшие до площадки S, пересекают ее в течение промежутка времени Behelyettesítve a (11.1), a kifejezés az átlagos sebesség = d / t, ahol t - az átlagos idő „rendezni az élet” a molekula, akkor lehet tekinteni, mint az átlagos idő hopping. „Balance” közlekedési molekulák révén S közben dt időintervallum egyenlő a területet Szorzás (11.3) által m tömeget egyetlen molekula, és elosztjuk Dt, megtalálják a tömegáram révén az S felület: .. Ie tömeg anyagok, melyek 1 átjut a területen S. koncentráció változtatása n2 - nl molekulák képviseli, mint a termék a dn / dx távolságban 2d közötti kiválasztott kötet: Egyenletben (11,4) szerinti helyére Dt (11.2) és (n2 - n1) A (11.5): áramlási kapcsolatot az S felület, amelyen keresztül azt át az úgynevezett fluxussűrűség: A terméket molekula tömeg azok koncentrációja az anyagsűrűség (részleges sűrűség): Ezt szem előtt tartva, van honnan (11,7) Ez a diffúziós egyenlet (Fick egyenlet), amely általában írásos formában: A „-” jel azt jelzi, hogy a teljes permeátum fluxus sűrűsége a diffúziós felé csökkentve a sűrűsége (az ellentétes irányban a gradiens sűrűség), D - a diffúziós koefficiens képest forgó példában a folyadék diffúzió bele egyenlő Amint látható (11,10), egy mértékegység a diffúziós együttható [m2 / s]. Diffúziós egyenlet felírható a nem csak a sűrűsége és a tömeges potokat fluxussűrűség és a tömegáram sűrűség, míg egyenletben (11,9) helyett a sűrűséggradiens használandó rendre koncentrációs gradiense vagy gradiens moláris koncentrációk: Einstein bebizonyította, hogy a diffúziós együttható arányos a hőmérséklet: És így, ahelyett, hogy (11.11) van Általános képletben (11.12) és a további um - a mobilitás diffúziós molekulák (részecskék), a kifejezés a mol. Általánosságban elmondható, a mobilitás a szórófelület részecske (molekula, atom, ion, elektron) nevezzük, és az együttható közötti arányosság a sebesség a részecskék és erőt u f. mozgó részecskék, abban az esetben, ahol a részecske egyéb erők (például, a súrlódás, vagy ütközés más részecskék) és mozog egyenletesen: Amint a (11.14), a mobilitás egység 1 m / (s • H). És az értéke is, és össze vannak kötve az Avogadro-állandó: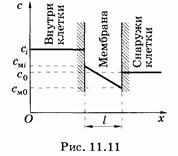
Mi transzformációs egyenlet (11.9) a biológiai membrán. Azt feltételezzük, hogy a részecskék koncentrációja diffundáló a membránon keresztül a membránhoz lineárisan változik (ábra. 11.11). A moláris koncentrációja a részecskék, és a sejten kívül egyenlő ci és C0. A moláris koncentrációja a részecskék a membrán változik a belső a külső rész, illetőleg, CMI, hogy SM0. Adott egy lineáris változás a molekulák koncentrációja, írhatunk
ahol L - a membrán vastagságát, majd ahelyett, hogy (11,11) van
Gyakorlatilag hozzáférhető meghatározza a moláris koncentrációja a részecskék nem tartozik a membrán (CMI és SM0) egy membrán: ketrecben (Cl), és a sejten kívül (c0). Úgy tartják, hogy a koncentrációk arányát a határ értékeket a membránban a koncentrációk arányát a szomszédos rétegek a membrán: SM0 / CMI = C0 / ci; ahonnan
ahol k - anyag megoszlási arány (részecskék) a membrán és a környező közeg (rendszerint a vizes fázis). Tól (11,18) a következőképpen
Behelyettesítve (11,19) a (11,17), van
ahol P - átbocsátási együttható. Ennek eredményeként, megkapjuk egyenletet a fluxussűrűség anyagok biológiai membránon keresztül diffúziós:
Mint ismeretes, létezik a membránpotenciál különbségek ezért a membrán van egy elektromos mező. Ez hatással van a diffúziós töltött részecskék (ionok és elektronok). Között a térerő E és a gradiens dj / dx a potenciális létezik egy ismert kapcsolat (lásd § 12.1.):
A felelős egy ion Ze. Egy ion erő hat; ható erő 1 mól ionok
Velocity irányított mozgása ionok arányos a hatóerővé [lásd. (11,4) (11,5)]
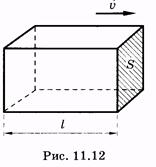
Ahhoz, hogy megtalálja áramlási anyag (ionok) kiosztani az összeg az elektrolit (ábra. 11.12), mint egy négyszögletes parallelepipedon alakú éllel, hogy számszerűen egyenlő a ion sebesség. Minden ionok paralelepipedon, 1 hogy átmennek a terület S. Azt is fog folyni F. A móljainak száma ezek az ionok megtalálhatók szorozni a térfogata a paralelepipedon (US) a moláris koncentrációja ionok:
anyag találni fluxus sűrűsége a következő képlet segítségével (11,24) és a (11,25):
Általában, ion transzport a két tényező határozza meg: a nem-egyenletes eloszlásuk, azaz koncentrációgradiens [lásd. (11.11)], és a hatása az elektromos mező [lásd. (11.26)]:
Ez a Nernst-Planck egyenlet. Kifejezés alkalmazásával mobilitás (11.12), transzformáljuk a egyenlet (11.27) a forma
Ez egy másik formája a Nernst-egyenlet Plank.
Használata Nernst-Plank egyenlet határozza meg a diffúziós fluxus sűrűsége attól függően, hogy az ion-koncentráció és az elektromos térerősség. Tegyük fel, hogy a rendszer állandósult állapotban, azaz a. E. j áramsűrűség állandó. Az elektromos mező a membrán venni, mint egy egységes, így a térerősség azonos, míg a potenciál lineárisan változik a távolsággal. Ez lehetővé teszi, hogy vállalja, hogy amennyiben JM - potenciális különbség a membránon keresztül. Leegyszerűsítjük a bejegyzést kifejezést az egyenlet (11.28):
- kiegészítő érték (dimenzió potenciális). Ami a (11,29) az egyenlet Nernst-egyenlet Plank formájában:
Mi választja el a változókat, és integrálják a következő egyenletet:
Hatáson (11,31), azt kapjuk,
Transform általános képletű (11,32), figyelembe véve a kifejezéseket (11,19) és (11.20):
Általánosságban elmondható, hogy a általános képletű (11,33) érvényes mind a pozitív (Z> 0, y> 0), és a negatív (Z <0, y <0) ионов. Однако для отрицательных ионов целесообразно видоизменить это выражение, подставив в него отрицательное значение безразмерного потенциала:
Osszuk a számláló és a nevező e kifejezés e - y:
Ha ezt a képletet, emlékeztetni kell arra, hogy a negatív Z értékek és y már szerepel a formula is, azaz y - .. A pozitív érték.
Egyenletek (11,33) és a (11,34) szerelt álló linket sűrűségű ionfluxust három változóval: 1) a permeabilitás a membránok egy adott ion, amely jellemzi az kölcsönhatását membrán szerkezetek ion; 2) egy elektromos teret; 3) a moláris koncentrációja ionok vizes oldatban körülvevő membrán (ci és c0).
Elemezzük a speciális esetekben egyenlet (11.33):
a) y = 0, ami azt jelenti, akár a Z = 0 (semleges részecskék), vagy hiányában a villamos térerősség a membrán (YM = 0), vagy mindkettő, és a másik:
Találunk korlátait az egyes tényezők.
Ez a bizonytalanság lehet nyitni a szabály alapján L'Hôpital:
Ebből kap, mint várnánk, az egyenlet (11,21):
b) az azonos moláris koncentrációja ionok a szemközti oldalon a membrán (ci = c0 = c) jelenlétében egy elektromos mező:
Ez megfelel a vezetőképessége az elektrolit (lásd. § 12,9). A semleges részecskék (Z = 0 és y = 0) J = 0;
c) ha a membrán impermeábilis részecskéket (P = 0), akkor természetesen, a fluxus nulla.