Szorzás vektorok és mátrixok száma

A termék egy mátrix

a chisloS úgynevezett mátrix az azonos méretű, ami. Ez a szabály érvényes a vektorok.

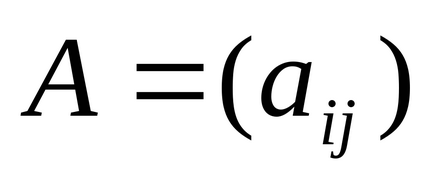
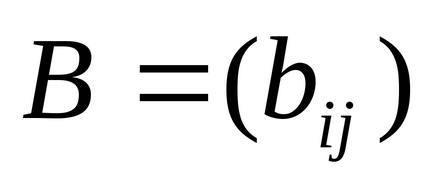
Felvenni a munkalap a nyomtatni kívánt a „szám” * „nevet

Szorzás vektorok és mátrixok.

A termék egy mátrix

méreta mátrixméretEz a mátrixméret, ahol . Négyzetes mátrixok.

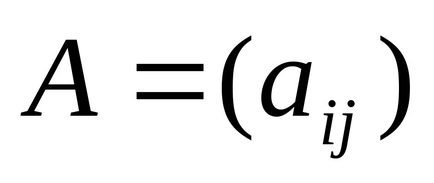
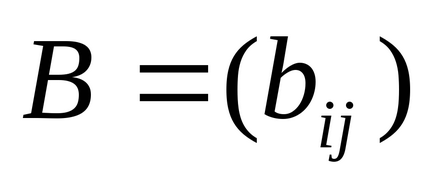
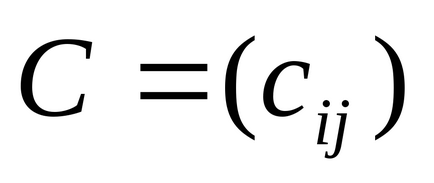
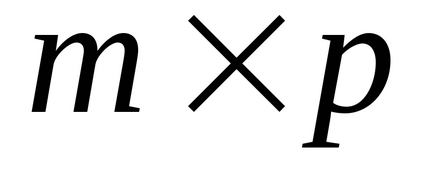
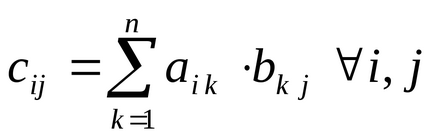
Rögzítése mátrix szorzás művelet lehet nyomtatni [Shift] * B = (egyenlő), vagy használja a kezelő Dot termék - skalár szorzat mátrixot Mátrix panel.

kétféle szorzás definiált vektorok:

- skalár szorzás (Dot Product)

, melynek eredménye egy szám, és

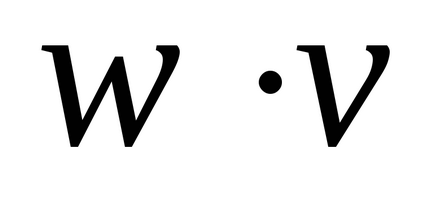
- vektor termék (szorzat)

, ami egy új vektort.

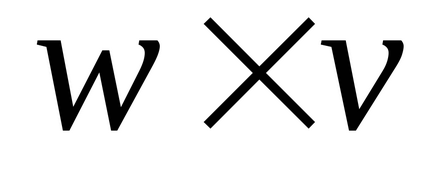
Munkalap skalár szorzata vektorok tárolt ugyanúgy, mint a mátrixok.

Vector terméket hivatkozás a Matrix panel, amelyben meg kell kattintani az egérrel opció

és töltse ki a sablont. Vektor olyan tényező legyen 3-dimenziós.

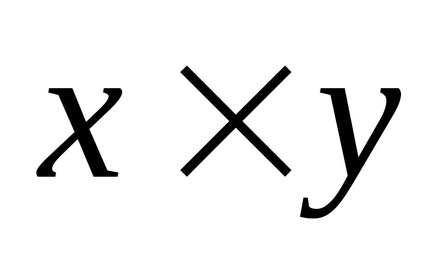
Átültetés vektorok és mátrixok.

Átültetés - transzformációs mátrix, ahol a kezdeti mátrix oszlopok vált sorok:

Átültetése a vektor - oszlop vezet felváltása vektor - egy sor azonos méretű:

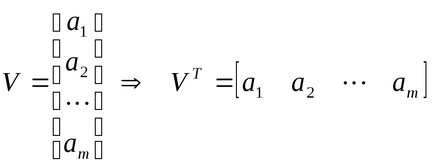
Példák az alapvető intézkedések a vektorokkal ábrán látható. 3.11. Körülbelül segítségével Mathcad, például svds (v). Utolsó (v) alább.

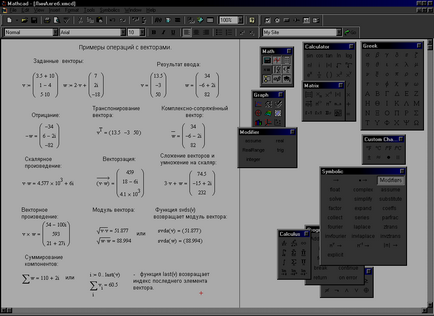
Ábra. 3.11. Példa műveletek vektorokkal.

3.2.5. A fordított mátrixba. Determináns egy mátrix.

mátrix

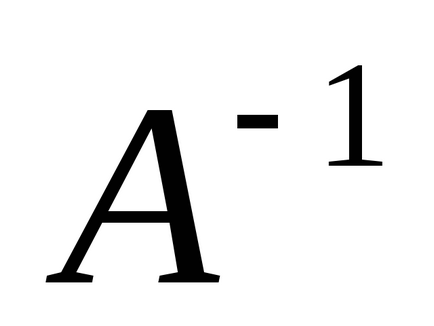
Ez az úgynevezett fordított matritsyA. ha akkor, amikor e - az identitás mátrix.

D

Egy négyzetes matritsyA fordított mátrix létezik, ha, és csak akkor, ha a meghatározója a mátrix elemei a vonal, nem nulla, azaz a . Meghatározói direkt és inverz mátrixok kapcsolja össze:.

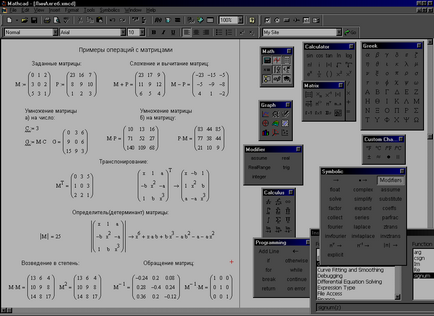
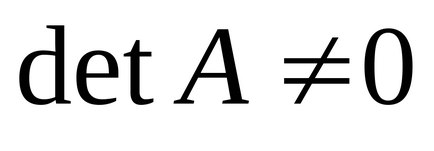
Ábra. 3.12. Példák cselekvések mátrixok.

Determináns (determináns) négyzetes mátrix

- szám (kijelölés) Jellemző tulajdonságait a mátrix. Kiszámítása mátrix determinánsa manuálisan - egy időigényes folyamat.

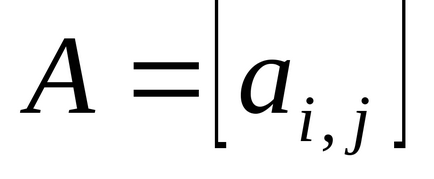
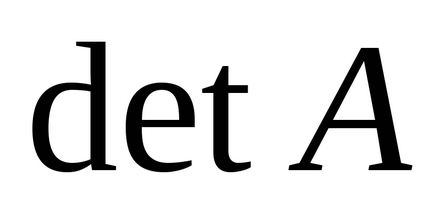
A Mathcad két lehetőség van kiszámítani a meghatározó.

Abban az esetben, ha a mátrix elemei az azonosítók meg kell adnia az azonos meghatározó sablont, töltse ki és küldje el az egér szimbolikus egyenlőségjel (balra nyíl) Szimbolikus panel (szimbolikus számítások), hogy megjelenítse az eredményt szimbolikus formában (ábra. 3.12).

3.2.6. vektorizálhatja operátor.

A Mathcad van egy készlet üzemeltető vektorizációs üzemben tartó (vektorizálhatja), amely különösen hasznos többször elvégezniük ugyanazt számítások.

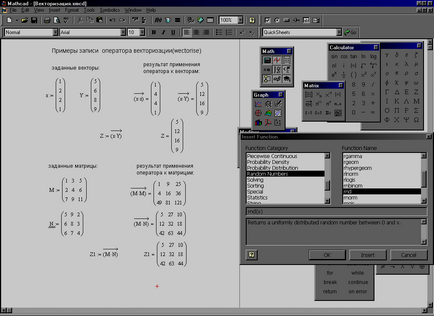
Ábra. 3.13. Példák vektorizáció szereplő bejegyzést.

A bevezetés a szolgáltató megszünteti a vita kapcsolatos skalár szorzata vektorok. Ennek lényege, hogy a vita a következő. Ha például, egy vektort megszorozzuk a skalár termék számának, kiderül egy új vektort, melynek minden eleme megszorozza ezt a számot, de ha a skalár megszorozzuk ugyanazt a vektort önmagával, az eredmény egy szám egyenlő a négyzetének összege a vektor elemek, nem egy vektort.

vektorizálás üzemeltető, ellentétben a skalár termék, megsokszorozza minden eleme VK (k = 1 ... n) a v vektor az elem az azonos számú (ugyanazt az indexet) a másik, vagy ugyanazon a vektoron, termelő új vektor az azonos hosszúságú n.

Írja vektorizálhatja szereplő két módja van:

- print Ctrl - (mínusz) „a neve az első operandus» [Shift] * «nevet a második operandus” = (egyenlő), és kattintson a bal egérgombbal;

- kattintson az egér opciót «f (M)» a mátrix Mátrix panelt, és kövesse a fenti lépéseket.

Operandusok vektorizáció üzemben lehet mátrix azonos méretű. Például, ha a nyomtatás M * M [lacuna] [Ctrl] - (mínusz) = (egyenlő), akkor megkapjuk egy új négyzetes mátrix azonos méretű, amelynek elemei egyenlő a termék minden egyes eleme a mátrix M önmagához.

Megjegyzés: Az a szám operandusok vektorizálhatja üzemeltető bármi lehet, nem feltétlenül egyenlő a kettő.