Meghatározza az első térsebesség a bolygó, ahol a tömeg és sugara a két

Állapota a problémát:

Határozzuk meg az első kozmikus sebességet a bolygó, a tömeg és a sugara kétszer nagyobb, mint a Föld.

№2.5.7 feladata a „Collection feladatok előkészítése a felvételi vizsgák a fizika UGNTU”

\ (R = 2R_3 \), \ (M = 2M_z \), \ (\ upsilon_1 -? \)

Megoldás:

Az első kozmikus sebesség - az arány, amit akar mondani a szervezetben, hogy ez lesz a társa bolygón. Megtalálható az alábbi szempontokat. Ha a mozgás egy műhold körpályán, a gravitációs erő adja a centripetális gyorsulás, így Newton második törvénye ad egy ilyen egyenlőséget:

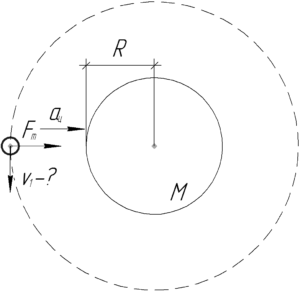
A gravitációs erő megtalálható a egyetemes tömegvonzás törvénye, tekintettel arra, hogy a magassága a pálya kicsi; ez egy földközeli:

műholdas centripetális gyorsulás, mozgó sebességgel \ (\ upsilon_1 \), egyenlő:

Az (1) egyenlet helyettesítheti az expressziós (2) és (3):

Ezért az első térsebesség lehet meghatározni a következő képlet:

A hipotézis \ (R = 2R_3 \) és \ (M = 2M_z \), ezért:

Elvileg kézhezvételét követően a képlet lehet mondani, hogy az első kozmikus sebességgel ezen a bolygón ugyanaz, mint a Földön. De mi „lesz elérni” a feladatot át.

Szaporodnak és osztódnak frakciókat root, hogy \ (R_3 \), akkor:

A kifejezés \ (>>>> \) a gyorsulás szabadesés \ (g \), közel a Föld felszínét, ennek eredményeként, van:

Emlékezzünk vissza, hogy a Föld sugara 6,4 · 10 6 m, ezért a számszerű válasz:

A: 8000 m / s.

Ha tetszik a probléma és annak megoldása, akkor ossza meg ismerőseivel Ezekkel a gombokkal.

Kapcsolódó cikkek

• Az első űrturista, Dennis Tito