Kockázat mérése az értékpapír-állomány

Home | Rólunk | visszacsatolás
A teljes kockázata a portfolió áll a piaci kockázat (nem diverzifikálható) és nem a piaci kockázat (diverzifikálható).
A legmélyebb hatást gyakorol a piaci kockázatot a GDP, az infláció, a kamatlábak és az átlag a gazdaság, a magas vállalati nyereség.
Nem piaci kockázat az egyéni jellemzőit egy adott eszköz. Ezt a kockázatot csökkenteni lehet a diverzifikáció.
Annak érdekében, hogy meghatározzák a kockázat az értékpapír-állomány szükséges meghatározni a mértékét a kapcsolatot, és a változás iránya a hozam a két eszköz. Például, ha az ár egy biztonsági emelkedik, a sebesség növekszik és egyéb értékpapírok, és fordítva, többirányú ármozgások vagy teljesen függetlenek egymástól.
Ahhoz, hogy meghatározzuk a kapcsolatát értékpapír használ ilyen mutatók a kovariancia és korrelációs együttható.
Covariance - egymással összefüggő közös variáció közül kettő vagy több jellemzője a folyamatnak. Covariance olyan intézkedés a variabilitás a közös a két értékpapír, mint a részvények.
Indikátor kovariancia a papírok A és B, a hozam a, amely jól ismert az időszakokban T adja meg:
Értelmezése a következő tényezők: a pozitív érték a kovariancia azt jelzi, hogy a hozam értéke ezeknek a részvények változik azonos irányban, a negatív kovariancia jelzi eltérő mozgások között a hozamok.
Értelmezze kovariancia nehéz, mert a nagy számértékek azonban méréséhez a kapcsolatot két eszköz segítségével a korrelációs együttható.
korrelációs számítást hajtjuk végre az alábbi képlet szerint:
Emlékezzünk vissza, hogy. - mutatók az értékpapírok kockázati (a becsült szórás)
A korrelációs együttható tól -1 és +1. +1 korrelációs érték azt jelzi, egy erős kapcsolatot, azaz a vagyon megy ugyanúgy. A -1 érték, ellenkezőleg, azt jelzi, többirányú, azaz a növekedés az egyik az eszközöket kíséri csökkenése a másik. A 0 érték azt jelzi, összefüggés hiánya.
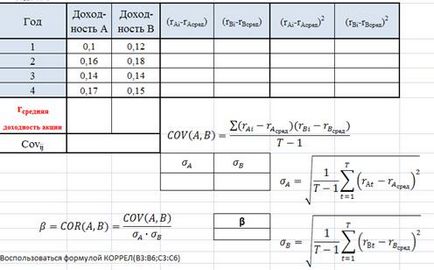
Együtthatók meghatározásához kovariancia és korrelációs két értékpapírok A és B
Markowitz modell alapja az a tény, hogy a hozam teljesítményét különböző értékpapírok állnak egymással: a növekedés a nyereségesség egyes értékpapírok van egy egyidejű növekedése az egyéb értékpapírok, és mások változatlanok maradnak, és a hozam a negyedik, éppen ellenkezőleg, csökken. Kockázat csökkentése megalakult a portfolió érjük el az épület egy portfolió számos különböző állományok.
A második módszer a kialakulását egy portfolió formulázzuk alapul Sharpe bezriskoy piaci hozam és kivetített nyereségesség.
A vetített hozam alapján határozzák meg a szakértői értékelés és a kockázat-mentes jövedelem mértékével mérve államkötvények, valamint a kevés vagy semmilyen kockázatot. A nyugati, a kockázat nélküli jövedelem mintegy 4-5%, akkor ugyanaz - 7-10%. A jövedelmezőség a teljes piac - a hozam a piaci index. Az Egyesült Államokban például az index a SP 500 és Oroszországban - az RTS index.
Most definiáljuk az együttható az egyes készletek # 946;, amely intézkedés a kockázat, összehasonlítva a jövedelmezőségére eszköz hozamok.
A kockázat szintje az egyes értékpapírok alapján határozzák meg ezeket az értékeket:
# 946; = 1 - az átlagos kockázati szint;
# 946;> 1 - magas kockázati szint;
# 946; <1 - низкий уровень риска.
Készletek magas béta (946 #> 1) nevezett agresszív, alacsony béta (# 946; <1) - защитными. Например, агрессивными являются акции компаний, чьи доходы существенно зависят от конъюнктуры рынка. Когда экономика на подъеме, агрессивные акции приносят большие прибыли. Например, акции автомобилестроительных компаний являются агрессивными. Инвесторы, ожидающие подъема экономики, покупают агрессивные акции, обеспечивающие больший уровень доходности в условиях растущего рынка, чем защитные. Акции компаний, чья прибыль в меньшей степени зависит от состояния рынка, являются защитными (например, акции компаний коммунальной сферы). Доходы таких компаний сокращаются в меньшей степени в условиях экономического спада. Поэтому использование защитных акций в периоды кризисов позволяет инвестору извлечь большую прибыль в сравнении с агрессивными акциями.
A kapcsolat a kockázata hozam modell szerint a hosszú távú eszközök értékelésére van leírva a következők:
- a várható hozam
- kockázatmentes hozamot, mint a szabály, államkötvények hozamainak
- A jövedelmezőség a teljes piac
Határozza meg a koefficiens értéke # 946; biztonsági A. A táblázat a biztonság és jövedelmezőség a teljes piac kilenc évig.
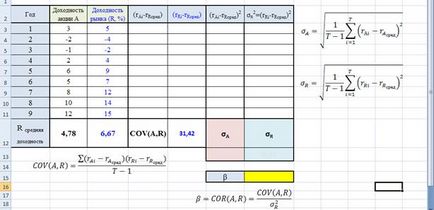
Ez az eredmény azt sugallja, hogy ha jövőre a piac növekedni fog a hozam 1%, akkor a befektető számíthat a hozam növekedés készletek átlagosan 0,706%.
Az ár a veszélye nélkül, 10%, a várható piaci hozam - 20%, p a részvény portfolió - 0, 8. Határozza meg az elvárt hozam a portfólió.
A kapcsolat a kockázata hozam modell szerint a hosszú távú eszközök értékelésére van leírva a következők:
- a várható hozam
- kockázatmentes hozamot, mint a szabály, államkötvények hozamainak
- A jövedelmezőség a teljes piac
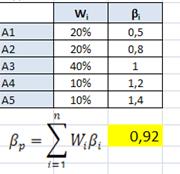
A portfólió öt eszközök. Fajsúly az első eszköz és a béta rendre 20% és 0, 5, a második - 20% és 0, 8, a harmadik - 40%, és 1, a negyedik - 10%, és 1, 2, az ötödik - 10%, és 1, 4. Határozza béta portfólió.
Beta portfolió - súlyozott átlag értékeinek béta eszközök szerepelnek a portfolió, ahol a súlyok az egységnyi tömege a portfolió. Ez a következőképpen számítjuk ki:
ahol: - béta portfolió
- béta i-edik eszköz;
- veri. a súlya az i-edik eszköz.
A portfolió két részvények - A és B aránya A részvények a portfolió 30%, béta - 0, 8, a nem-piaci kockázatot - 15%. Az akció fajsúlya 70% -kal egyenlő, béta 1, 3, nem piaci kockázatot - 8%. A piaci kockázat 10%. Mi a veszélye, hogy a teljes portfolió képviseli a szórást?
A teljes kockázata az eszköz lehet osztani divesifitsiruemy és nondiversifiable
ahol: - a piaci kockázat az eszköz,
- nem piaci kockázat az eszköz.
A kockázat, amelyre az egy eszköz birtoklása is két részre oszlik. Az első komponens - ez a piaci kockázatot. Úgy is nevezik szisztémás vagy nem diverzifikálható vagy nem specifikus. Ez együtt jár az állam a piaci feltételek, általában jelentős események, mint például háború, forradalom. Nem lehet kizárni, mert a veszélye, hogy a teljes rendszert. A második rész - a nem piaci, specifikus vagy diverzifikálható kockázat. Ez együtt jár az egyes funkciók egy adott eszköz, hanem az állam a piac egészére. Például a tulajdonos minden raktáron van veszteség kockázata miatt a sztrájkot a cégnél, hogy ki ez a papír, a hozzá nem értés a vezetők, és így tovább. N. Ez a kockázat diverzifikálható, mert lehet majdnem nullára csökkent segítségével portfóliódiverzifikáció. Amint azt a tanulmányok nyugati tudósok, a portfolió álló 10-20 jól megválasztott eszközök szinte teljesen megszünteti a nem piaci kockázatot. Széles körben diverzifikált portfolió tartalmaz szinte kizárólag a piaci kockázatot. Rosszul diverzifikált portfolió, mind a piaci és nem piaci kockázatokat. Így a befektető csökkentheti a kockázatot csak a szint a piacon, ha a forma széles körben diverzifikált portfolió.
Markowitz modell alapja az a tény, hogy a hozam teljesítményét különböző értékpapírok állnak egymással: a növekedés a nyereségesség egyes értékpapírok van egy egyidejű növekedése az egyéb értékpapírok, és mások változatlanok maradnak, és a hozam a negyedik, éppen ellenkezőleg, csökken.
- a biztonsági megtérülési feltételezett várható jövedelmezőség;
- a biztonsági kockázattal szórása visszatérés;
- azt feltételezzük, hogy a történelmi adatok számításához használt kockázat és a megtérülés, teljes mértékben tükrözi a jövőbeli értékek a hozam;
- mértéke és jellege közötti kapcsolat értékpapírok által kifejezett lineáris korrelációs együttható.
A gyakorlati alkalmazás modell Markowitz alábbi képletek segítségével optimalizálja a részvényportfólió:
· Hozamú értékpapírok:
ahol T - száma már megfigyelések a biztonsági visszatér.
· A kockázat a biztonsági (formájában értékelése szórás)
statisztikai értékelése közötti korrelációs együttható a két index hozamú értékpapírok:
- hozamú értékpapírok i és j a t.
N tekinthető az értékpapír kiszámításához szükséges korrelációs együtthatók.
Még az optimalizálási modell, kiválasztja az optimális portfolió nem kézzel. Hogy oldja meg a problémát optimalizálási Hasznos az Excel.