Brown-mozgás
A koncepció a Brown-mozgás
Törvényszerűségei Brown-mozgás és a tudomány alkalmazása
A koncepció a Brown-mozgás szempontjából az elmélet a káosz
A mozgalom egy biliárdgolyó
Integration determirovannyh fraktálok és a káosz
A koncepció a Brown-mozgás
Brown-mozgás helyesen Brown-mozgás, termikus mozgás anyag részecskék (mérete több mikron vagy ennél kisebb), szuszpendálunk a folyadék vagy gáz részecskék. Brown-mozgás az oka számos nem-kompenzált impulzusok által megkapott Brown-részecske a környező molekulák egy folyékony vagy gáz. Nyitott P. Browne (1773 - 1858) 1827-ben A látható, csak mikroszkóp alatt szuszpendált részecskék függetlenül mozognak, és leírják komplex cikcakkos pályáját. Brown-mozgás nem gyengíti az idő, és nem függ a kémiai tulajdonságai a közeg. Brown-mozgás intenzitása együtt növekszik környezeti hőmérséklet és csökkenő annak viszkozitás és a részecskeméret.
Következetes magyarázata Brown-mozgás adta A. Einstein és M. Smoluchowski a 1905-1906 alapján a molekuláris-kinetikus elméletét. Ezen elmélet szerint, a folyékony vagy gáz molekulák állandó hőmozgást, impulzusokkal különböző molekulák eltérő nagyságát és irányát. Ha a felület a részecskék környezetbe helyezzük alacsony, amint az a Brown-részecske, majd fúj által tapasztalt hogy a részecske a környező molekulák nem lesz pontosan kompenzálni. Ezért, ennek eredményeként a „bombázás” a molekulák egy Brown-részecske jön véletlenszerű mozgásban megváltoztatja a nagysága és iránya a sebessége körülbelül 10 14-szor másodpercenként. Ha megfigyeljük a Brown-mozgás van rögzítve (lásd. Ábra. 1) helyzetét a részecske szabályos időközönként. Természetesen a megfigyelések a részecske nem mozog egy egyenes vonal, de a kapcsolat az egymást követő pozíciók egyenesekkel ad feltételes képet a mozgás.
Gumigyanta részecske Brown-mozgás a vízben (1. ábra)
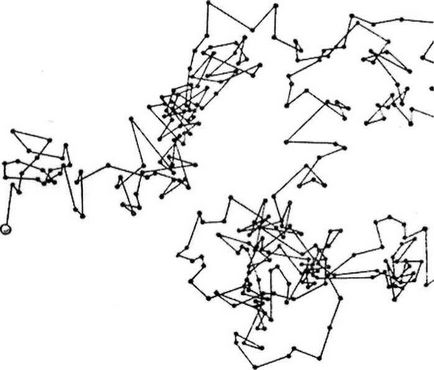
Törvényszerűségei Brown-mozgás
Törvényszerűségei Brown-mozgás egyértelműen demonstrálják alapvető rendelkezéseinek a molekuláris kinetikus elméletét. A teljes képet a Brown-mozgás által leírt Einstein törvény átlagos négyzetes elmozdulását a részecske bármely irányban x. Ha az idő két mérés között zajlik egy kellően nagy számú részecske ütközések a molekulák azután arányos ezúttal t:
Itt, D - a diffúziós koefficiens, ami által meghatározott az ellenállás által kifejtett viszkózus közegben ott mozgó részecske. Egy gömb alakú részecske sugarú, és ez egyenlő:
ahol k - Boltzmann állandó T - abszolút hőmérséklet, h - a dinamikus a közeg viszkozitása. Elmélet Brounskogo véletlenszerű mozgás magyarázza a befolyása a részecskék véletlenszerű mozgását, erők a molekulák és a súrlódási erők. A véletlenszerű jellege erő azt jelenti, hogy a kereset az időintervallum t 1 teljesen független a cselekvés intervallum t 2. Ha ezen intervallumok nem fedik egymást. Az átlagos idő elegendően nagy erőnek nulla, és az átlagos elmozdulását Brown-részecskék is nulla. Következtetések elmélet Brown-mozgás kiváló egyezést a kísérleti általános képletű (1) és (2) igazoltuk mérések J. T. Svedberg és Perrin (1906). Ezek alapján arányok kiszámítása kísérletileg Boltzmann állandó és az Avogadro-szám szerint a kapott értékek al. Methods. Az elmélet a Brown-mozgás szerepe volt az alapja a statisztikus mechanika. Ezen túlmenően, ez is egy gyakorlati jelentősége. Először is, a Brown-mozgás korlátozza a mérési eszközök pontosságának. Például, a határ a pontosság jelzések határozzuk jitter tükör galvanométer tükör, mint a Brown-részecske bombázzuk levegő molekulák. Brown-mozgás határozza meg a jogszabályok véletlenszerű elektronok mozgása, ami zajt az elektromos áramköröket. Dielektromos veszteségek dielektrikumokban magyarázzák véletlenszerű mozgások a molekulák dipólusok, dielektromos komponenseket. Véletlen mozgását ionok elektrolit oldatok növeljék elektromos ellenállás.
A koncepció a Brown-mozgás szempontjából az elmélet a káosz

Brown-mozgás - van, például, véletlenszerű és kaotikus mozgása porrészecskék vízben szuszpendáljuk. Ez a fajta mozgás valószínűleg egy aspektusa fraktálgeometria amelynek legnagyobb gyakorlati haszna. Véletlen Brown-mozgás termel frekvenciadiagram hogy lehet használni előrejelzésére dolgot, beleértve a nagy mennyiségű adatok és statisztikák. Jó példa erre az ára gyapjú, ami Mandelbrot jósolta útján Brown-mozgás.

Frekvencia diagramok létrehozott rajzoló alapján Brown számokat is lehet alakítani zene. Természetesen ez a fajta fraktál zene nem zene, és tényleg fárad a hallgatót.
Feltartotta a diagram véletlen Brown számokat megtalálja Dust Fractal hasonló ahhoz, ami itt látható példaként. Amellett, hogy használni Brown mozgás fraktálok fraktálok, és fel lehet használni létrehozására a tájat. Sok sci-fi filmek, mint a Star Trek Technology Brown mozgás létrehozásához használt idegen tájak, mint a hegyek és magas fennsíkok topológiai mintát.
Ezek a technikák nagyon hatékonyak, és megtalálható a könyvben a Mandelbrot fraktál geometria a természet. Mandelbrot létrehozásához használt egy sor Brown fraktál vonal a part és a szigetek kártyák (ami valójában csak véletlenszerűen pont a kép) a madártávlat.
MOZGALOM biliárdgolyó
Bárki, aki valaha felvette a dákó snooker, tudja, hogy a legfontosabb, hogy a játék - pontosság. A legkisebb hiba a szög a kezdeti hatása gyorsan vezethet hatalmas hibát labda helyzetét után néhány ütközések. Ez az érzékenység a kezdeti feltételekre nevezett káosz tűnik leküzdhetetlen akadályt számára, aki azt reméli, hogy megjósolni vagy irányítani a pályáját a mozgás a labda után, több mint hat vagy hét ütközések. És nem hiszem, hogy a probléma abban rejlik, hogy a por az asztalon, vagy bizonytalan kézzel. Sőt, ha használja a számítógépet az épület egy modellt, amely egy biliárdasztal, nem rendelkezik sem a súrlódás, embertelen pontosan szabályozható a helymeghatározás a végszó, még mindig nem tudja megjósolni a pályára a labdát a hosszú idő!

Meddig? Ez részben attól függ, pontosságát a számítógépen, de nagyobb mértékben az alakja az asztalra. Ahhoz, hogy teljesen kerek asztal lehet kiszámítani, hogy körülbelül 500 ütközések rendelkezéseinek hiba körülbelül 0,1 százalék. De meg kell változtatni az alakját az asztalra úgy, hogy lett legalább egy kicsit rossz (ovális), és kiszámíthatatlan útvonal meghaladja a 90 fokot, miután a 10 ütközések! Az egyetlen módja, hogy egy képet az általános viselkedése biliárdgolyó újjáéledő net asztalra -, hogy ábrázolják a fellendülés szög vagy ív hosszának megfelelő egyes ütemet. két egymást követő növekedése egy fázis-térbeli minta látható itt.

Minden egyes régió vagy csuklópontjaihoz szétszórják labda viselkedés előforduló egyik kezdeti feltételek. Terület Pictures, amely megjeleníti az eredményeket bármely adott kísérletben, az úgynevezett attraktor régió egy adott kezdeti feltételek. Amint látható formában a táblázat ezekhez a kísérletekhez alkalmazott a fő része attraktor területeket, amelyeket szekvenciálisan ismételjük a csökkenő méretű. Elméletileg egy ilyen önhasonlósági van, hogy örökké, és ha növeljük a szám egyre több, kapnánk mind az azonos alakú. Ez az úgynevezett nagyon népszerű ma, a szó fraktál.
BEILLESZKEDÉSE SZÁNDÉKKAL fraktálok, és a káosz
A fenti példák determinisztikus fraktálok látható, hogy azok nem mutatnak kaotikus viselkedés, és hogy azok valóban nagyon kiszámítható. Mint ismeretes, használja fraktál káoszelmélet, hogy újra, vagy talál mintát annak érdekében, hogy viselkedésének előrejelzésére sok rendszer jellegű, mint például az a probléma, madárvonulásban.
Most lássuk, hogyan is történik. A fraktál úgynevezett fa Pitagorasz, nem tartozik ide (ami mellesleg nem találta Pythagoras és semmi köze a Pitagorasz-tétel) és a Brown-mozgás (ami kaotikus), próbáljuk, hogy a szimuláció egy igazi fa. Ésszerűsítése levelek és gallyak a fa nehéz, és véletlenül, és valószínűleg nem valami egyszerű ahhoz, hogy képes emulálni egy rövid program 12 sort.
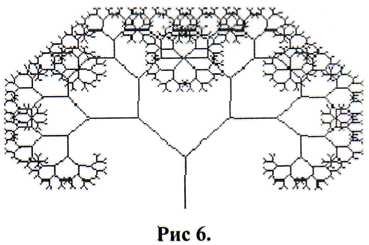
Először létre kell hoznia egy Püthagorasz fa (a bal oldalon). Ez szükséges ahhoz, hogy egy vastagabb törzse. Ebben a szakaszban a Brown-mozgás nem használt. Ehelyett minden szakasz most egy szimmetria vonalat a téglalap, ami lesz a törzs, és ágazik ki.
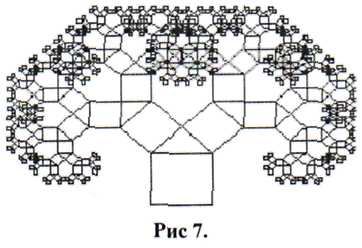
De az eredmény még mindig úgy néz ki, túl formális és rendezett. A fa még mindig nem úgy néz ki, mint egy élő. Nézzük alkalmazni néhány ismerete determinisztikus fraktálok, amelyet az imént vásárolt.
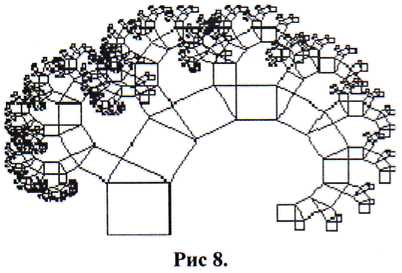
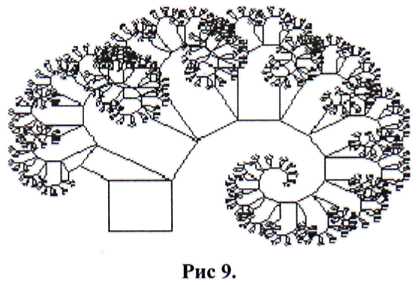
Most a Brown-mozgás lehet használni, hogy egy random rendellenesség, amely megváltoztatja a számot, a kerekítési őket legfeljebb két bit. Az eredeti 39 bites decimális számok kerültek felhasználásra. Eredmény (balra) nem úgy néz ki, mint egy fa. Ehelyett, úgy néz ki, mint egy gyanús horgon.
Talán kerekítve 2 számjegy volt túl sok? Ismét használja Brown-mozgás, ezúttal felfelé kerekítve 7 számjegy. Az eredmény még mindig úgy néz ki, mint egy horog, de ezúttal formájában logaritmikus spirál!
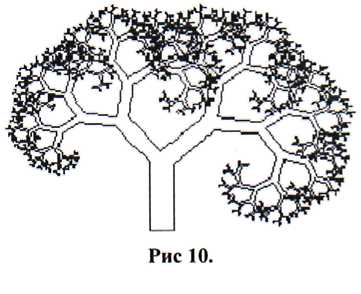
Mivel a bal oldali (amely minden páratlan szám) nem befolyásolja a horog véletlen zavar által termelt Brown-mozgás, kétszer alkalmazva az összes számot a bal oldalon, és csak egyszer kell a számokat a jobb oldalon. Lehet, hogy elég lesz, hogy megszüntesse vagy csökkentse a hatása a logaritmikus spirál. Így a szám kerekítve 24 bit. Ezúttal az eredmény - tetszetős számítógépes kaotikus emulációs valódi fa.
Kapcsolódó művek:
Mozgást, mint a módja, hogy
BEVEZETÉS 3 2 1 meghatározást a "MOVE". Korreláció az anyag és a mozgás. PROBLÉMA forrású mozgalom. Mozgás és a nyugalom február 4 alapvető formák. ügyet. Folyamatok előforduló a szervetlen természetű (brounovskoedvizhenie stb), a biológiai folyamatok (mutagenezis és mtsai.).
Anyagi pont. referencia szervezetben. A referencia-rendszer. Kinematikai joga mozgás a
elméletek és kísérleti igazolása. Brounovskoedvizhenie. A súlya és méretei a molekulák. brounovskoedvizhenie - folyamatos kaotikus mozgása mikroszkopikus részecskék oldhatatlan a folyadékban. Dvizheniebrounovskih részecskék miatt véletlenszerű mozgás.
microheterogeneous van rendszerek, amelyek részt vesznek brounovskomdvizhenii. mint amelynek eredményeként a részecskék a diszperz fázis. EK és a kinetikus energia a részecskék résztvevő brounovskomdvizhenii. Az állam a kolloid rendszer függ.
Tanfolyam >> Informatika
Az alkalmazás a káoszelmélet a világban 2.3.4 Brounovskoedvizhenie és annak alkalmazása 2.4 Integration determinisztikus fraktálok. tudás ma. 2.3.4 Brounovskoedvizhenie Brounovskoedvizhenie és alkalmazása - jelentése például, keverd.
az olyan jelenségek, mint brounovskoedvizhenie. diffúziós, ozmotikus nyomást. Részecskéket. mozgás. Így brounovskoedvizhenie következménye a termikus mozgás diszperziós közeget és a közvetlen tükrözi a statisztika. Brounovskoedvizhenie.