Elmélet és jelfeldolgozás matlab a tos, 7. oldal

miközben Z - nulla értékek vektora, p - pólus-vektor, k - erősítés.

Számára, hogy a pole - nulla képviselete folyamatos rendszer átviteli függvénye ribtínukleinsavval

bomlik egyszerű frakciókat az átviteli függvény képviseletében a arányban két polinom. Itt levonások tárolja a r vektor. pólusok - a vektor p. szert - k. Format [B, A] = maradék (Z, P, K) három bemeneti argumentumokat és két kimeneti rendszer átalakítja a pólus-zérus átviteli függvény a reprezentáció.

Építése a tranziens válasz (stepresponse) rendszer végezhetjük megadásával

Hasonlóképpen ábrázoltuk impulzusválasz (impulseresponse) rendszer

Annak megállapításához, a válasz (output) rendszer egy tetszőleges bemeneti parancs jelet használnak lsim (...).

Példa. Mi határozza meg a rendszer kimenő jel az átviteli függvény

és a bemeneti jel.

>> n = [2 0]; % A számláló és a nevező az átviteli függvény

>> t = linspace (0,5,301); % Beállítása az időintervallum

>> u = cos (2 * pi * t); input%

>> [y, x] = lsim (n, d, u, t); % A kimeneti jel

>> xlabel ( 'idő, sec');

A grafikonok a bemeneti és kimeneti jelek

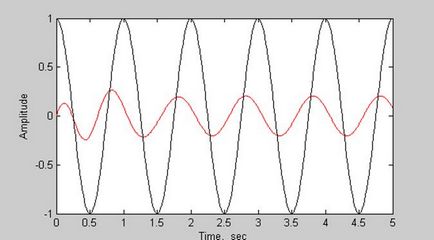
Frekvencia tulajdonságok és a grafikonok

MATLAB-függvények kiszámítására és építése grafikonok frekvencia jellemzői:

FFT (x) - kiszámítja a diszkrét Fourier-transzformáltja x vektor által a gyors Fourier transzformációs algoritmussal (FFT)

IFFT (x) - kiszámítja az inverz diszkrét Fourier-transzformáció x vektor segítségével FFT

fftshift - termel műszakban konverziós FFT tartományban (0, 2π) intervallumban (-π, π)

freqs (n, d) - kiszámítja a frekvencia jelleggörbét (frequencyresponse) a rendszer folyamatos átviteli függvény n (k) / d (s)

freqz (n, d) - kiszámítja a frekvencia karakterisztikával (diszkrét) átviteli funkció a rendszer n (Z) / d (Z)

Bode (n, d) - épít Bode diagramját folyamatos rendszer egy rendszer funkciója n (k) / d (s).

Csomagolja (P) - korrigálja a fázisszögek az egydimenziós tömb a P-elemek az átmenet során
Az érték-π.

Példa az építés a frekvencia karakterisztika a rendszer az átviteli függvény

set (GCA 'FontName', 'Times New Roman Cyr', 'betűméret', 8)

cím ( 'Amplitude - chactotnaya harakterictika')

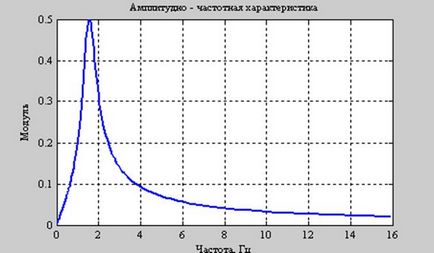
Példa Bode diagram és építésére a impulzusválasz

„Building% pólusok és nullák diagram

FFT () függvény a jelfeldolgozási feladatok használják, talán jobban, mint bárki más. A komputer diszkrét Fourier transzformáció (DFT) a vektor x a kifejezést

ahol - a hossza a x vektor.

Ugyanez a funkció a formátum

kiszámítja az N - pont diszkrét Fourier-transzformáció. Ha a hiányzó elemeket a tömb x egészítik nullákkal (zeropad). Ha, akkor további elemek eldobjuk.

A funkció x = IFFT (X) kiszámítja az inverz DFT-szekvencia X. A funkció x = IFFT (X, n) kiszámítja az N - pontos inverz DFT.

Kiszámításához az FFT () és IFFT () Fast Fourier Transform használt algoritmusok (FFT). Ez az algoritmus a legjobb teljesítményt, ha a szekvencia hossza egyenlő az x erejét 2. Ezért kívánatos használni szekvenciák amelynek hossza 2 hatványa.

% A számítási eljárást és gyártásakor spektrumok

% A jeleket FFT () függvény

N = 128; % Pontok száma

Ts = T / (N-1); % Mintavételezés

t = 0: Ts: T; % időszeletet

tau = 2; % Impulzus-időtartam

X = rectpuls (t, tau); Négyszög impulzusokat előállító%

részterület (311), plot (t, x), grid% ütemezés jel

set (GCA, 'FontName', 'Arial Cyr', 'fontSize', 8)

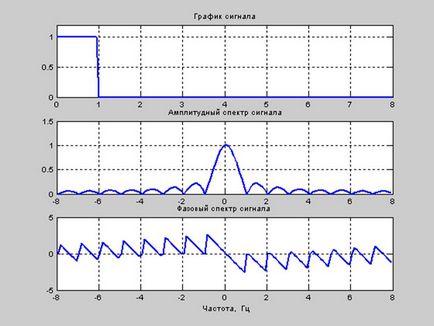
title ( 'jel tartás)

Fmax = 1 / Ts; % Maximális frekvencia

df = 1 / T; % Frekvencia felbontás

X = FFT (X, N); % FFT

Xp = fftshift (X); % Frekvencia eltolás

részterület (312), plot (F, ABS (Xp) * Ts), grid

set (GCA, 'FontName', 'Arial Cyr', 'fontSize', 8)

cím ( „amplitúdó spektrumú jel”)

% S = sinc (f * tau / 2) * tau / 2; % A Fourier-transzformáció a jel

részterület (313), plot (F, szög (Xp)), grid

set (GCA, 'FontName', 'Arial Cyr', 'fontSize', 8)

xlabel ( 'Frequency, Hz')

cím ( „fázis spektrum jel”)

Elemzés lineáris diszkrét rendszerek

y = CONV (x, h) - kiszámítja a konvolúciót a H és X szekvenciák. Használata konvolúciós számított kimenőjel diszkrét rendszer impulzus h és egy bemenő x zéró kezdeti feltételek.

Conv parancs is lehet használni, hogy szaporodnak a polinomok CONV (a, b) - a termék a polinomok által képviselt vektorokat a és b együtthatók.

Az átviteli függvény egy diszkrét rendszer

Ez képviseli MATLAB vektor együtthatók a számláló és a nevező

dstep és dimpulse csapat számított rendre és az impulzus tranziens válasz a rendszer

»Num = [10, 0]; den = [1 0,07 -0.6];