Lab 4 m definíciója lövedéksebesség útján egy torziós inga ballisztikai
- a tanulmány a működési elve a ballisztikus inga és a törvény védelme perdület;
- kísérleti függőség ellenőrzése között a fizikai mennyiségek jellemző torziós rezgések;
- kísérletesen meghatározott állandó rugalmas erői torziós és szögletes ballisztikai inga tehetetlenségi;
- kísérleti meghatározása segítségével ballisztikus inga sebességváltozás golyók.
Eszközök és kellékek:
- Timing-ballisztikus inga 02 automatizált időzítő időszakok és millisekundomerom tüzelő eszköz.
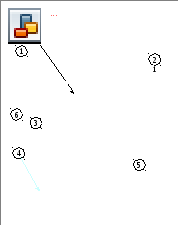
1. ábra - Általános nézet berendezése Timing 02
Az installáció:
1) ballisztikus inga (1) felfüggesztve egy acél izzószál. Az inga két átmérősen elhelyezett acélrúd, amelyek mozgatható rengeteg M. Az egyik rúd van rögzítve töltve agyagot célt;
2) a tüzelő eszköz (2);
3) a fényelektromos jelátalakító (3);
4) ciklusok száma az automata számláló (4);
5) Automatikus millisekundomera (5);
6) a szögletes skála (6).
Szerelési lehetővé teszi a közvetlen mérését az alábbi mennyiségeket: az oszcilláció időszakban a ballisztikus inga; szögletes amplitúdója torziós rezgések ballisztikus inga.
Podgotovkapribora dolgozni és mérések
A készülék tartalmazza a kulcsfontosságú hálózati „hálózat”. Az egyensúlyi helyzet ballisztikus inga úgy van beállítva, hogy az megfelel-e nullára szögskálájának.
Mérési időszak kolebaniyballisticheskogo inga.
Mozgatható terhek rögzíti a távolságot R1. által javasolt tanár. Zero leolvasott nyomja meg a „Reset” gombot, óvatosan döntse meg a ballisztikus inga egy adott tanár szög stabil egyensúlyi helyzete és felszabadulását. Amikor elérte a ballisztikus inga szám „kilenc” rezgések (9), nyomja meg a „STOP” gombot. Ebben az esetben a gróf idő után megszakad tíz teljes oszcilláció. Az az időszak, oszcilláció egyenlő időt osztva a rezgések száma (n = 10). T = T / N.
Szög amplitudypri teljesen rugalmatlan hatását egy golyó a célt plastilinomballisticheskogo inga.
Állítsa be a rakomány áthelyezéséhez a javasolt rendelet (a rendező a tanár). Töltse speciális golyó töltő rugós szerkezet úgy, hogy a vezetékes és után tartott rugó. Ballisztikus inga Gyurmazáras célt kell lennie a nyugalmi állapotban megfelelő a nulla helyzetét az szögskálájának. Megnyomása kapu tüzelő eszköz, regisztrálja a maximális szöget, amellyel a eltért ballisztikus inga.
Égetés után, a golyó kell maradnia ragadt és agyag célt. Ez a tapasztalat sikeresnek tekinthető. Ha a golyó lepattant, a telepítés kell hozni az eredeti állapotában, és ismételje meg a tapasztalat.
Ballisztikus ötlet sebességét mérő egy golyót egy golyó az ütközés alatt az ingával szögsebessége ballisztikus inga változik igen jelentős és szögletes mozgás jelentéktelen és elhanyagolható. Természetesen ez a feltétel teljesül abban az esetben az inga tömege sokkal nagyobb golyó súlyát.
Kezdősebesség mérésével határozzuk meg a maximális hajlásszöge az inga után rugalmatlan ütközések a golyót. A folyamat a rugalmatlan ütközések az ingával ismertet egy golyó a törvény alapján a természetvédelmi impulzusmomentum (ebben a folyamatban a mechanikai energiát nem konzervált!), És az azt követő eljárás mozgás leírható a törvény mechanikai energia megmaradás.
Azonban bármilyen elméleti modell csak egy hozzávetőleges leírást a fizikai helyzetet, mivel figyelmen kívül hagyva a hatása más hatások fordulnak elő a kísérletben. De ha az igazi neglect az elméleti modellben nem változik a végeredmény több mint 1/20 a valós értéket, akkor ez elméleti modell a fizikai laboratóriumi gyakorlaton egészen elfogadható, és lehetővé teszi, hogy meghatározza a kívánt fizikai mennyiség.
A mi esetünkben, figyelmen kívül hagyjuk a kis elmozdulás az inga tömegközéppontja az ütközés után a golyó, rugalmas hullámokkal, amely így keletkezik, és ennek megfelelően a mechanikai energiát újraelosztás a rugalmas és torziós rezgések. Is figyelembe csillapítatlan torziós rezgések, elhanyagolva a légellenállást és energiaelnyelő rugalmas rezgések a föld rugalmas drót akasztó és így tovább. N. Azonban a javasolt elméleti modell lehetővé teszi, hogy elég jó eredményeket.
1. meghatározása Cél ballisztikus inga tehetetlenségi nyomatéka (Io) ikoeffitsienta rugalmas erői torziós (C).
1. Állítsa a mozgatható tömeg M terhelések azonos D1 távolságban a forgási tengely. Elutasítása ballisztikus inga szögben φ
20 °, a T1 periódusban intézkedés oszcillációk. Ismételje meg a tesztet 3-szor, és kiszámítja az átlagos értéket T1.
2. Állítsa be a szállított áruk tömege M távolból d2 és ismételje tapasztalat (lásd. 1. hivatkozás). Sokkal jobb, ha az értékek a D1 és D2 különböznek, amennyire csak lehetséges.
3. A rendszer egyenletek 1) és 2), hogy ebben az esetben a numerikus értékek T1. T2. d1. d2. Keresse Io és C.
4. Számítsa ki a relatív hiba meghatározásakor a tehetetlenségi nyomaték és a rugalmas együtthatója a torziós erők
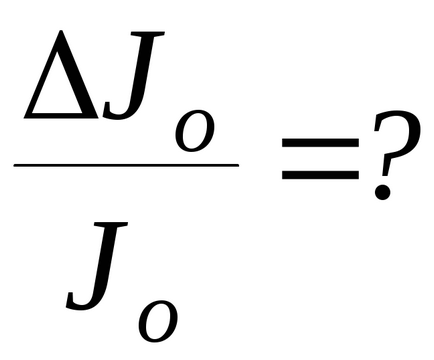
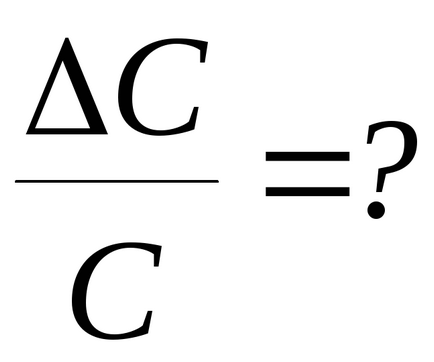
Bonyolultsága miatt a matematikai kifejezés meghatározására ez a hiba, akkor egy egyszerűsített számítási lehetőség. Ehhez a relatív hiba értékeket közvetlenül határozza meg (M, d, T) hozott egyenlő:
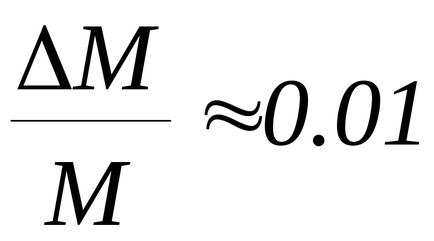
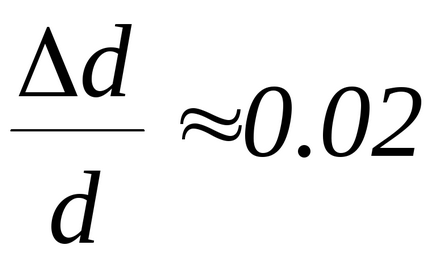

Töltse képfelvevő eszközzel és a beállítási mozgatható terhelések (M) az azonos távolságra d3. hogy egy lövés, miközben mérjük a maximális eltérés a ballisztikus inga φmax és a távolság a forgástengelye a tömegközéppont golyók
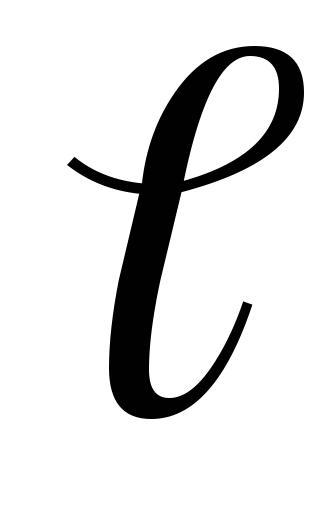
A törvény megőrzése perdület ad:
ahol vn a sebessége a lövedék,
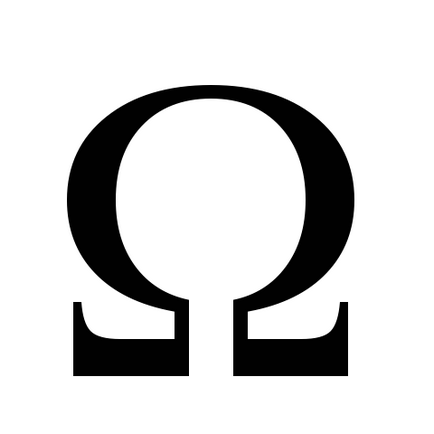
A törvény a mechanikai energia megmaradás:
A egyenletrendszert 3) és 4) keresse és Vn. Angle φmax így szükség van, hogy helyettesítse radiánban:
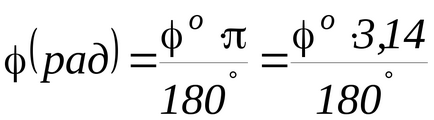
ahol φ a - fokban.
Számoljuk ki a relatív hiba a sebesség golyók
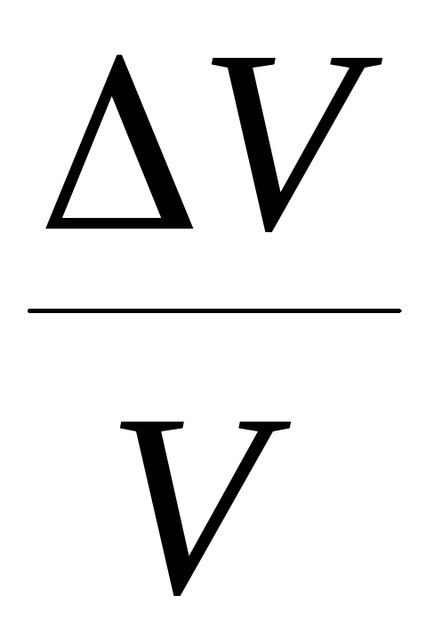
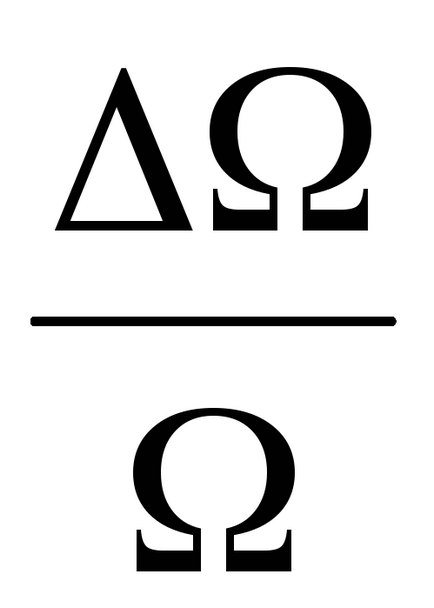
Relatív hiba értékek közvetlenül határozza meg (m. Fordulat.
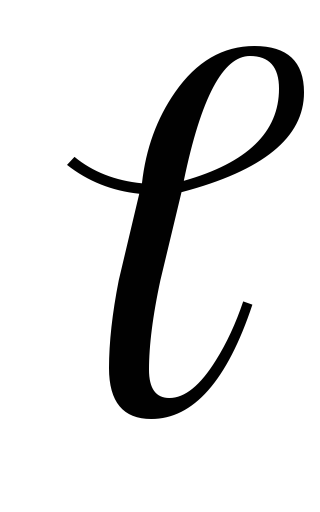
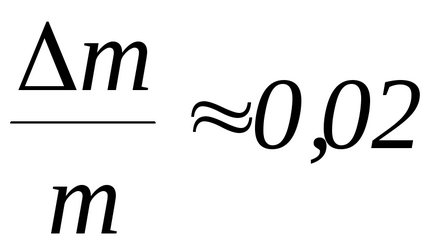
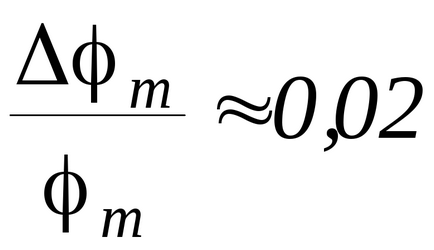
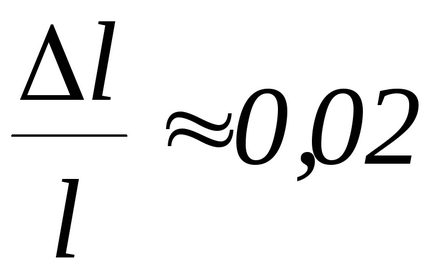
Alkalmazás. Meghatározása lövedék sebességű ballisztikus inga (elméleti anyag)
Ha bejön egy golyót a célt, gyurma, ballisztikus inga szerez szögsebességgel és elhagyja az egyensúlyi helyzet, oszcilláló tengelye körül. Feltételezzük, hogy a kezdősebesség idején ütközés és tengelyére merőleges az inga karja. Ha ez a feltétel nem teljesül, akkor amellett, hogy a forgási, akkor is izgatott és rezgési szabadsági fokkal az inga, azaz a. E. A tengely inga elkezd rezegni.
Mivel kezdősebesség merőleges a cél sík, az impulzusmomentum golyók:
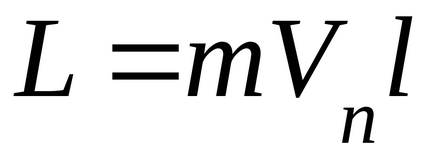
ahol
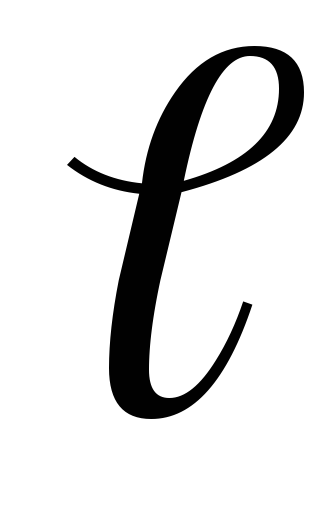
Impulzusnyomatékhajtómű a rendszer az ütközés után adja meg:
ahol I - tehetetlenségi nyomatéka a rendszer ütközés után a lövedék egyenlő: I = Io + 2M
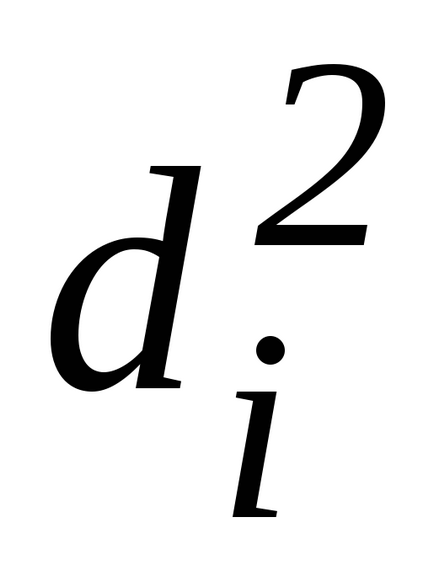
- szögsebesség a rendszer az ütközés után.
Puncs tekinthető teljesen rugalmatlan, mert becsapódáskor egy cél golyó beragadt gyurmából. Ebben az esetben a törvény megőrzése perdület változások:
Így az ütközés után ballisztikus inga szerez szögsebességgel. Amikor az inga mozgása akkor fog működni a nyomaték okozta torziós deformációját acélhuzal egy inga, amely egyenlő:
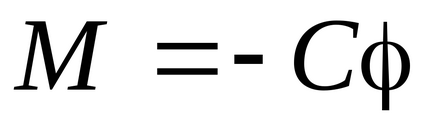
ahol a C - állandó rugalmas erői torziós huzal;
φ - a szög eltérése az inga az egyensúlyi helyzetből.
A „mínusz” jel azt jelzi, hogy ha φ> 0, M <0. Поэтому в момент соударения угловая скорость будет максимальной, а в дальнейшем она будет уменьшаться до нуля.
A további mozgás, ha nem veszi figyelembe a légellenállás, a törvény mechanikai energia megmaradás. A legnagyobb alakváltozás időpontjában a szögsebesség nulla és a potenciális energiája maximális és egyenlő
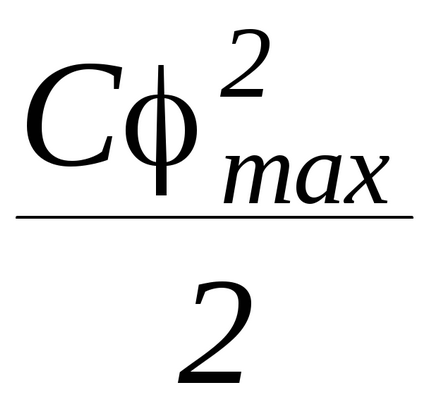
Így a törvény az energiamegmaradás felírható:
ahol φmax - a legnagyobb elfordulási szögét az inga.
Segítségével törvényei megőrzése perdület a (n-1) és az energia (n-2), kapjuk:
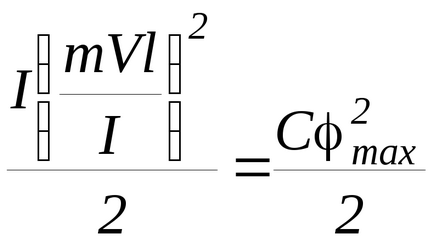
. Azaz kezdősebesség az ütközés előtt a ballisztikus inga által adott kifejezést:
Adjuk meg a perdület. Hogy ezt az értéket használjuk a laborban?
Mi az az elv, a ballisztikus?
Mi természetvédelmi törvények ebben a vizsgálatban alkalmazott?
Adj egy meghatározást a tehetetlenségi nyomaték.
Fogalmazza meg a tétel a Steiner-Huygens.
Hogyan állapítható meg, a tehetetlenségi nyomatéka a ballisztikus inga?
Hogy a szórás szögét ballisztikus inga becsapódáskor a lövedék és a rezgési periódus, ha egy nagyobb tehetetlenségi nyomatéka?
Mi történik, ha a golyó szögben síkjára merőlegesen a cél?
Kap képlet meghatározására lövedéksebesség, ha miután a ballisztikus inga rugalmatlan ütközés által eltérített a maximális szöget φ.