Hiperbola, mivel a aszimptotákkal, analitikus geometria
Ha túlzás egyezik a valós és a képzetes fél tengely, azaz, a = b, akkor a közötti szög aszimptotákkal egyenlő 2arctg (b / a) = 2arctg1 = π / 2, azaz a Ez egyszerű. Az ilyen túlzó hívják szabályos. Kivéve a kanonikus koordinátarendszer, amelyben a koordináta tengelyeket egybeesik a szimmetriatengelye a hiperbola, valamint figyelembe véve más, amelyek tengelyei vannak aszimptotákkal. Levezetjük egy egyenlet túlzás ebben a koordináta-rendszer, amely jelöli Oxy. Legyen i, j - a keretben. és i 'J' - Ox'y kanonikus frame koordinátarendszer „(8.1 ábra.).
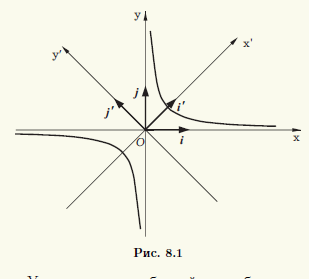
Kanonikus koordinátarendszer képest elforgatva Oxy rendszer szöget π / 4. Ezért (lásd. 4.2) i '= √2 / 2i + √2 / 2J, J' = -√2 / 2i + √2 / 2J .Znachit koordináták x 'y' kanonikus koordinátarendszer kifejezve koordinátái x, y az azonos együtthatók: x '= √2 / 2x + √2 / 2y, Y' = -√2 / 2x + √2 / 2y
Egyenletben négyzetes hiperbola kanonikus koordinátarendszerben formában van (x „) 2 - (y”) 2 = a 2., ahol egy - valós (ugyanaz a képzeletbeli) tengely mentén a hiperbola. Cseréje Ebben az egyenletben a kanonikus változók x, y, azt kapjuk, 1/2 (x + y) 2 - 1/2 (x - y) 2 = a 2. vagy
Egyenlet (8.1) nevezzük az egyenlet a hiperbola a aszimptotával.
Megjegyzés 8.1. Egyenlet xy = -a 2/2 beállítja konjugátum hiperbola derékszögű hiperbola (8.1).
Példa 8.1. Megtaláljuk a csúcsainak koordinátáit, gócok, illetve azokat az egyenleteket a aszimptotái hiperbola xy = - 8 és a kivitelezést.
Ez az egyenlet egy egyenletet a konjugátum aszimptotákkal négyzetes hiperbola. Ezért, a koordináta-tengelyek, azaz Direct X = 0, y = 0, vannak annak aszimptotákkal. Erre a hiperbola -a 2/2 = -8, azonban a 2 = 16, és a = b = 4. De majd c = √ (a 2 + b 2) = √ (április 2 2 + 4) = 4√2, és mivel a megnevezések csúcsok és gócok, találunk: a (-2√2; 2√2), B (2√2; - 2√2), F1 (-4; 4), F2 (4, -4) ( ábra. 8.2).