A mértéke csúcsok
(Helyi) mértéke vagy (vegyérték)
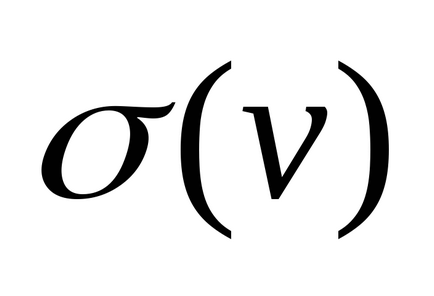
Hacsak másképpen nem jelezzük, a hurok kétszer számít a számítás a vegyérték a csúcsok.
Egy gráf helyes (vegyértékű r) vagy r-valens gráf (szabályos, egyenletes), ha az összes csúcsainak foka egyenlő.
Vertex nevezzük izolált. ha ez nem egybefüggő bármelyik a gráf, vagy ami ugyanaz, neintsindentna szegélyét. A mértéke a vertex egyenlő 0.
A csúcs, amelynek mértéke egyenlő 1, az úgynevezett lóg (terminál). Rib intsindentnoe lógó felső, az úgynevezett terminál.
1. elfogadása (lemmao kézfogás): A n-gráf összege fok minden csúcs van kétszeresével egyenlő az élek számát (azaz igaz):
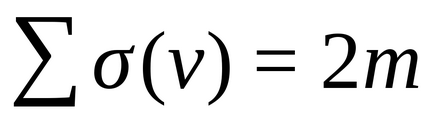
Következmény 1. Egy tetszőleges gráf páros számú csúcsainak páratlan fokú.
Következmény 1. Az élek száma a teljes gráf egyenlő
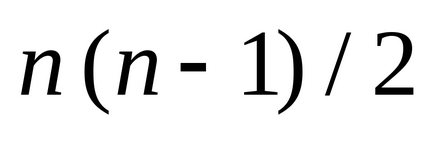
Az OP-oszlopon két (helyi) szinten tetején:
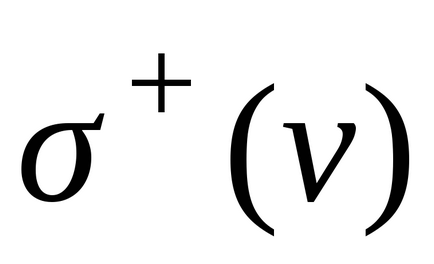
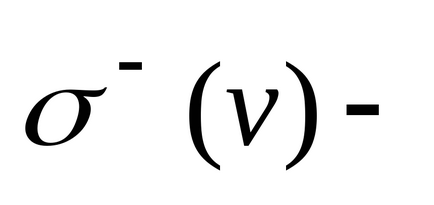
2. igénypont szerinti összege hatáskörét valamennyi a gráf vagy-egyenlő az élek száma a gráfban, és ezáltal, egyenlő egymással. m - az élek számát.
Rész, részleges grafikon és részgráfok
A grafikon H nevezzük egy része a G gráf (
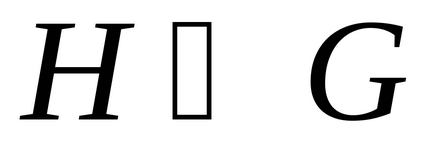
Ha a készlet a gráf H és G gráf egybeesik, majd grafH úgynevezett részleges gráf gráf részleges grafikon H nevezzük fedél n-gráf Ha minden csúcsa a G gráf intsindentna legalább egy éle a NA (azaz, ha G nincs izolált csúcsot, akkor a részleges grafikon, amely csak nem kell izolált csúcsok).
részgráf
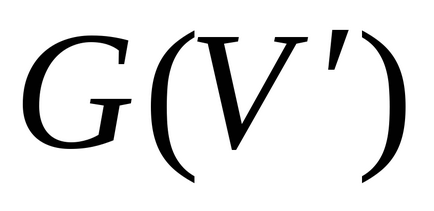
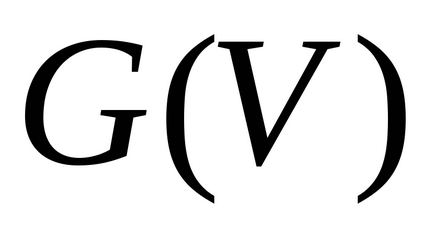
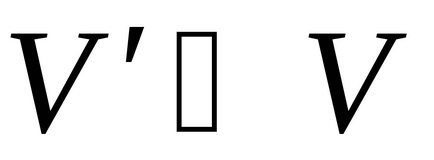
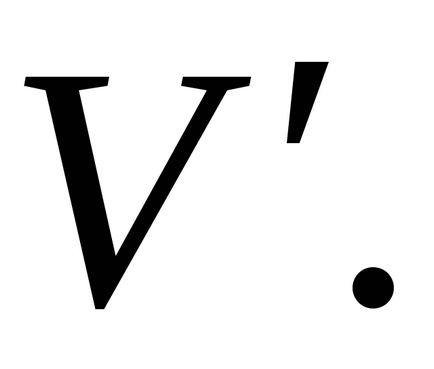
(részgráf
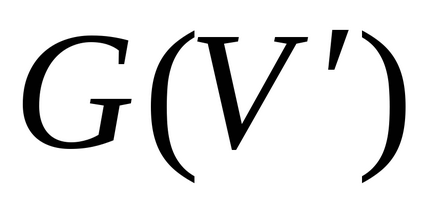
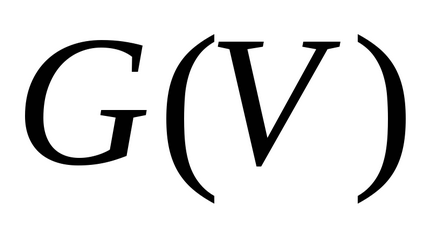
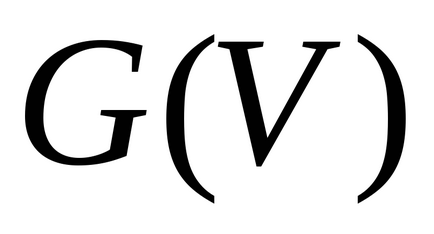
Manipulálása alkatrészek száma
kiegészítés

, ;
összeg

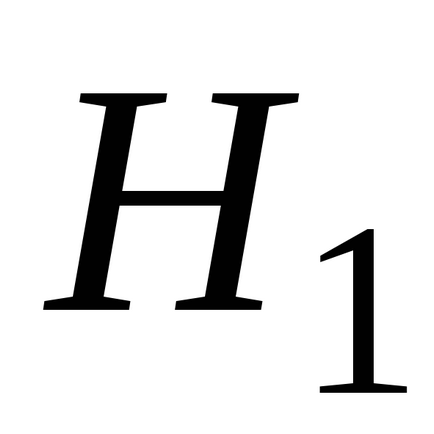
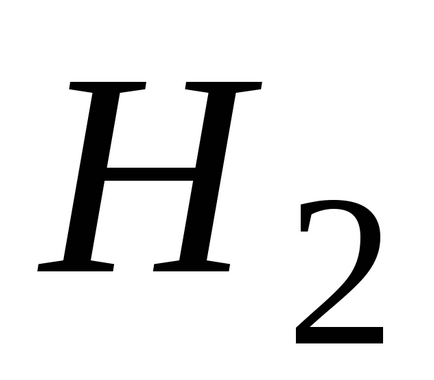
termék
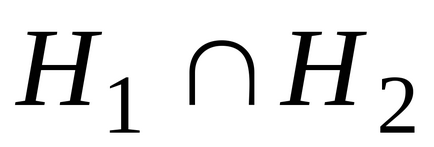
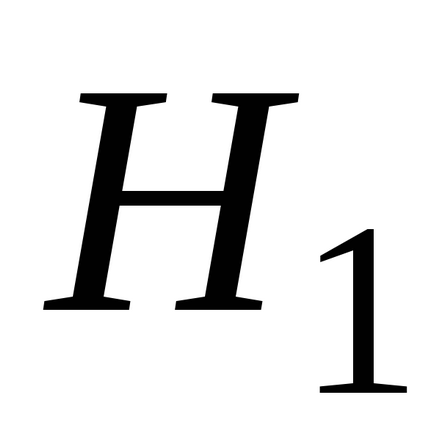
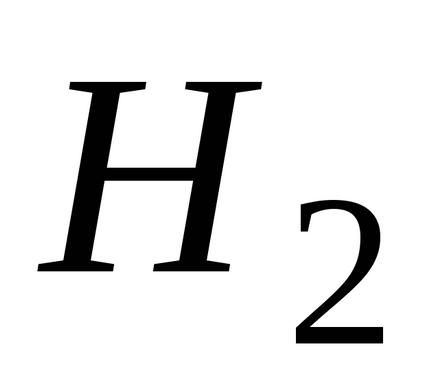
alkatrészek
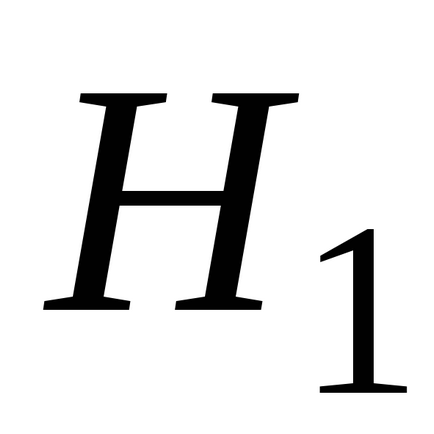
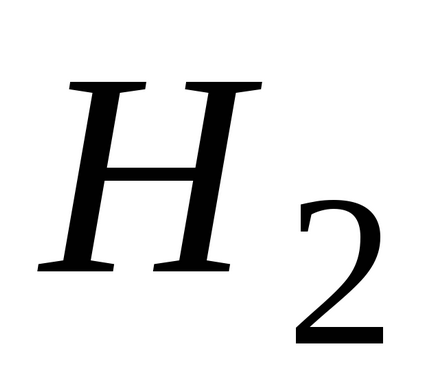
, .
alkatrészek
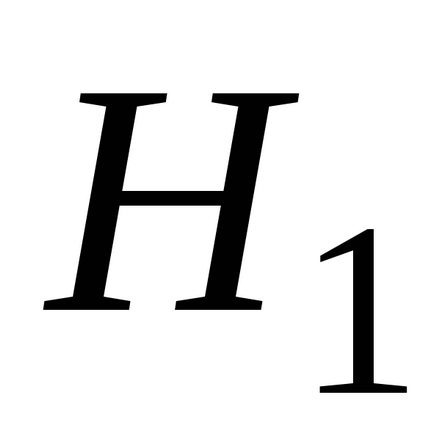
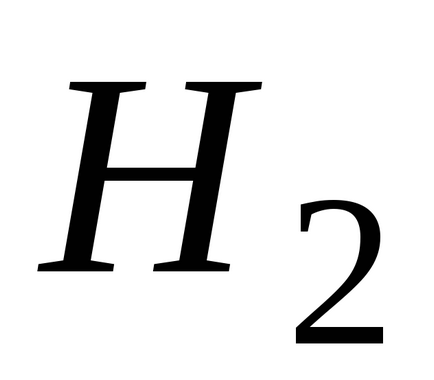
.
Ha, akkor az összeg

Grafikonok és bináris kapcsolatok
R arány, halmazán megadott V, egy-az-egyhez megfelelés G irányított gráf (R) nélkül többszörös éleket csúcshalmaza V, ahol a borda
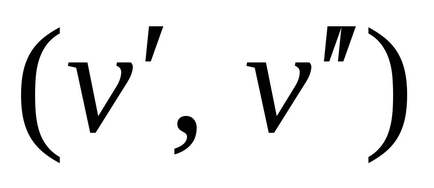
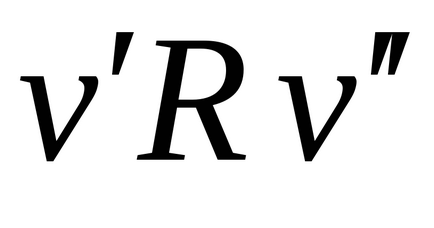
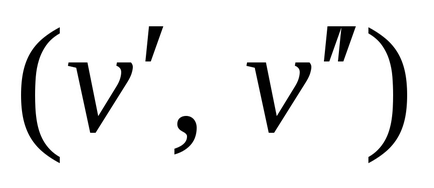
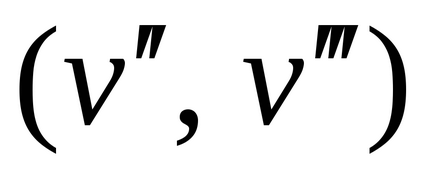
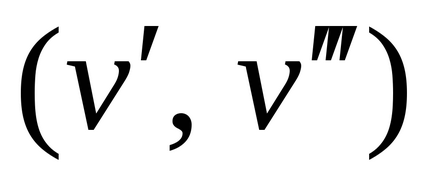

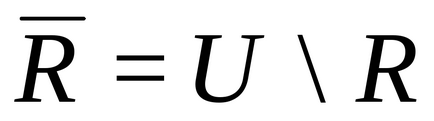
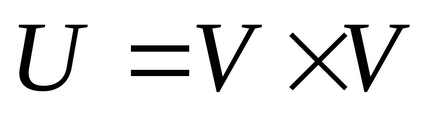
G gráf (

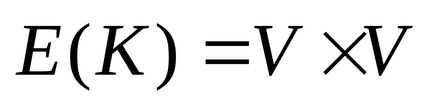
fordított arányban gráf G (
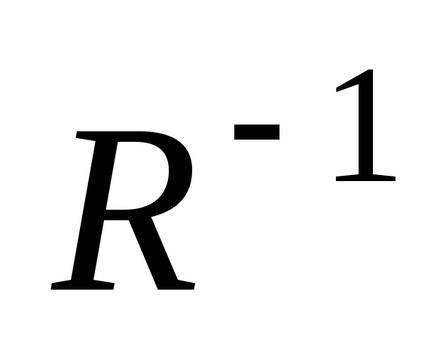
Count kombinálva két kapcsolatok meghatározott V,
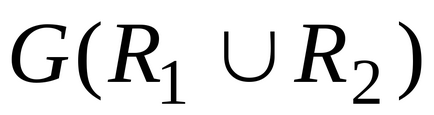
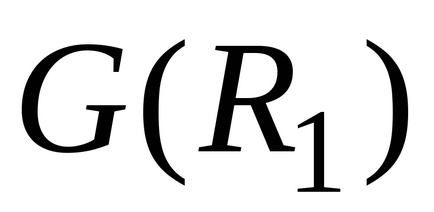
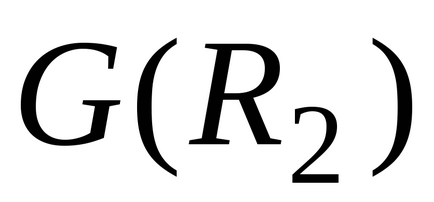
.
kereszteződés grafikonja kapcsolatok V és
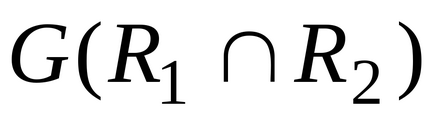
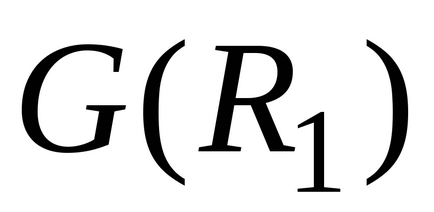
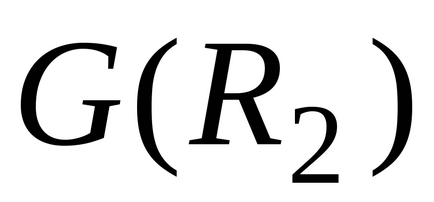
.