Operations Research Előadások, bemutató (p
Azaz, X * is optimális megoldást.
1. Tétel jelzi elvének megoldása LP problémák: ahelyett, hogy a tanulmány a végtelen sok lehetséges megoldás is szükséges vizsgálni, véges számú sarkok.
1.3. Grafikus módszer megoldására LP problémák két változó
Dana LP probléma két változó
A grafikus módszer megoldás alapja a grafikai lehetőségek SDT probléma megtalálni benne az optimális megoldást.
1. Építsd SDT probléma megoldások, mint a kereszteződés régiói minden, a meghatározott korlátok. SDT lehet egy konvex sokszög; konvex sokszög határtalan domént; üres terület; gerenda; szegmens; egy pont. Ha SDT az üres halmaz, a probléma nem oldja meg az összeférhetetlenséget átlagos rendszer korlátaira.
2. Ha a SDT nem üres, határozza meg az irányt a növekedés a célfüggvény Z (X).
Egy tetszőleges rögzített értékét sík egyenlete meghatároz egy egyenest, amely a vonal szintjét az objektív függvény - a vonal, amelyen a célfüggvény a probléma tart állandó érték. Az általános nézet az a szint egyenes egyenletéből: s1x1 + s2x2 = l, l = const. Minden szinten vonalak párhuzamosak egymással. Az normális. VozrastaniyaZ irány az az irány (X).
Így, a második lépésben az épület egy normál szint vonalak és az egyik szintvonalakat (amelynek egy közös pont a SDT).
3. A vonal párhuzamosan mozognak a szint a normális irányba maximalizálására, az ellenkező irányba, a probléma, hogy egy minimum. Egy bizonyos ponton, akkor elviszi a határhelyzet 1) rendelkezik legalább egy közös pontja van a SDT 2) SDT lesz ugyanaz félsíkban vonalhoz képest szinten. Ez a szint az úgynevezett referencia vonal egy egyenes vonal. SDT bármilyen LP probléma nem több, mint két referencia vonalak, amelyek közül az egyik lehet az optimális megoldás.
4. Ha az elmozdulás szinten SDT sorban a megfelelő irányba vonalszintű végtelenhez tart, a probléma nem optimális megoldás, tekintettel a célfüggvény korlátos. Írja Z (X) →.
5. Ha a probléma van egy optimális megoldást jelenlétére feltétlenül szükség van, hogy megoldja egyidejűleg az egyenleteket vonalak határoló SDT és a közös pont a referencia vonalat.
6. Számítsuk ki a értéke a célfüggvény az optimális megoldást.
Attól függően, hogy az SDT és az objektív függvény Z (X) LP probléma lehet egy egyedülálló megoldás, végtelen számú megoldások optimális megoldások (lásd. Ábra. 1, 2, 3).
Az 1. ábra mutatja a szint a vonal válik kétszer támogatásával kapcsolatos sokszög döntéshozatal. A minimális érték Z (X) megvalósíthatók t max - .. A t C.
A 2. ábra egy támogatási tétel egybeesik az egyik a sokszög oldalainak megoldásokat. Az optimális megoldás bármely konvex lineáris kombinációja szegmens AE pont.
A 3. ábra nem korlátozódik SDT felfelé értékek Z (X).
Példa 1. Oldjuk grafikusan LP feladat:
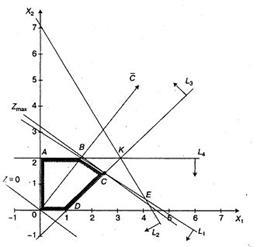
Építsünk Solution sokszög (4. ábra). Ehhez X10X2 koordinátarendszerben a síkon ábrázolja a határvonalak:
3x1 + 2x2 = 13 (L2);
Figyelembe bármely pontján, például a származási hozunk létre néhány félig sík határozza meg a megfelelő egyenlőtlenség. Half-által meghatározott síkban a egyenlőtlenségeket, a 4. ábrán mutatjuk nyilak. Solutions OABCD sokszög.
Építési szintű görbét Z = 3x1 + 4x2 = 0 és a vektor gradiens. Egyenes Z = 0 lépés párhuzamosan magát az irányt a vektor. Ábrából következik, hogy a 4. kapcsolatban sokszög való utalás ebben a sorban válik a C pontban, ahol a függvény a maximális érték.
A lényeg metszéspontjában az L1, L3. Annak érdekében, hogy meghatározzák a koordinátákat megoldani az egyenletrendszert:
Optimális terv célkitűzései x1 = 2,4; x2 = 1.4. Behelyettesítve az értékek x1 és x2 a lineáris függvény, ezt kapjuk:
.
1.4. Az oldatot lineáris programozás problémák a szimplex módszer
Hoz LP problémákat a kanonikus
Ha egy matematikai modellt a LP probléma a következő:
akkor azt mondjuk, hogy a probléma bemutatott kanonikus alakban a minimum (maximum).
Több kompakt jelölés:
(1) és (2), - a felvételt a koordináta kanonikus LP probléma.
Vector jelöléssel a kanonikus probléma:
Mátrix jelöléssel kanonikus probléma:
Bármilyen LP probléma csökkenthető kanonikus a következő szabályok szerint.
1. Átmenet feladatról feladatra max min (és fordítva) módosítja a jel a célfüggvény
Az eredeti és a kapott problémák ugyanolyan optimális megoldást X * és az értékeket a célfüggvény az oldatban csak abban különbözik jel.
2. Ha vannak korlátozások között egyenlőtlenség, majd bevezetésével további nem-negatív változók alakítjuk saját
A célfüggvény a további változók kerülnek bevezetésre nulla együtthatók, egyáltalán nem tudják befolyásolni a jelen esetben, a Z érték (X)
3. Ha egy változó xk korlátozás nincs a jelet, hogy helyébe (a célfüggvény és minden korlátok) a különbség a kettő között új, nem-negatív változó: hol.
1. példa, így a kanonikus formában (legalább) az LP probléma:
1. Most viszont, hogy a feladat legalább
2. Tegyünk minden korlátozás behatárolja szintező rendszer változók x 4, X 5, X 6. A rendszer egyenletek írhatók formájában.
.
3. A kanonikus alakja a felvétel LP problémát az összes változó szerepel a rendszer korlátozásainak negatívnak kell lennie. Tegyük fel, hogy hol.
Behelyettesítve ezt a kifejezést a rendszer korlátai, és a célfüggvény és írásban változók növekvő sorrendben az index, megkapjuk a LP probléma bemutatott kanonikus formában:
A működési elve a szimplex módszer
LP problémák döntés alapján a szimplex módszer teljes keresést a sarokpontok célozzák javítása SDT értéke a célfüggvény.
Először is érvényes megoldás megfelel az egyik sarokpont SDT. Kockás, amely annak szögletes pontot, hogy található ugyanazon a határon SDT, mint a jelenlegi sarokpont (egy kétdimenziós SDT - ugyanazon az oldalon egy sokszög, egy háromdimenziós - ugyanazon szélén a poliéder, stb ...).
Belátható, hogy az átmenet az egyik szögpontja SDT egy másik (szomszédos) megfelel a változás alapján egyetlen változó. Ilyen esetben az azt jelenti, hogy az egyik nem-bázikus változók (mely nulla érték) szerepel az alapja m. E. Fokozott, és az egyik alapvető változók nullára csökken, azaz a. E. kizárt alapján. A választás az ilyen változók végzik bizonyos szabályok szerint, amely a leggyorsabb javulás a célfüggvényt.
Ha egyik szomszédos sarokpontjait a célfüggvény nem javult, majd az oldatot befejeződött; SDT tényleges sarokpont megfelel az optimális megoldást a problémára. Ha vannak szomszédos sarokpontok SDT, melyek az objektív függvény javul, a folyamat az egyik közülük, amelyek a leggyorsabb javulás érhető el az objektív függvény. Egy új sarokpont SDT folyamat megismétlődik. Számbavételét sarokpontok fordul, amíg nincs optimális megoldás talált m. E. Amíg a sarokpont SDT, melyek sem a szomszédos pixelek értéke a célfüggvény nem javult.
A módszer az úgynevezett simplex, hogy az, hogy a tolerancia a megoldások, amelyeket figyelembe vettek a korai fejlődési szakaszában a módszer, volt egy egyszerű (egyszerű) formájában (1. ábra) ..:
1.Zadacha csökken kanonikus formában.
2.Stroitsya simplex eredeti tábla, és határozza meg a kezdeti kivitelezhető oldatban (kezdeti szöget bezáró pont).
3.Vypolnyayutsya simplex konverziós táblákat megfelelő sarokpontjait a rendezési SDT illetve az optimális megoldásokat.
Tekintsük a végrehajtása ezen algoritmus megoldása lineáris programozási feladatok:
1. Mi átírni a probléma kanonikus formában, hozzáadjuk ismeretlenek:
2. Írja le az első simplex táblázat:
Ha az utolsó sor (a számok C1, C2 ....) nincs negatív együtthatók a lúgos oldatot (amikor a szabad ismeretlenek x1 = ... = xn = 0) optimális. Valóban, ha a növekedés 0 közül legalább az egyik a szabad ismeretlenek, akkor a függvény csökken.
Tegyük fel például, -C1 <0, тогда, увеличивая число х1 будем получать большие значения функции. Если число a11>0, akkor az egyenlőség minden más szabad 0 ismeretlen x1-ra emelhető, legfeljebb száma b1 / a11. Ha a11 0, akkor az egyenlőtlenség nem korlátozhatja a növekedés a száma x1 (x1, akkor lehet növelni, mint szükséges). Ezért, ha minden együttható a11, ..., AK1 nem pozitív, akkor x1 nőhet a végtelenségig, és ugyanabban az időben, a funkció is növekedni fog a végtelenségig. Ebben az esetben az optimális megoldás nem.
3. esetekre korlátozódik, ahol az első oszlopban a számok között a11, ..., AK1 pozitív együtthatók: míg az x1 értékre növeljük x0 = min. Hagyja perc alatt éri el a sorban, és legyen i1 = 1 Most pedig, hogy az alap, fordítására x1 xn alapján helyett + 1. Kapunk egy új szimplex tábla, amelyre a függvény értékét növeli a számát C1 x0> 0.
Egy új szimplex táblázatot, ha az utolsó sor nem negatív együtthatók megfelelő bázikus oldat optimális (a funkció a forma, ahol a számok, ..., 0, és ezért számának növelése x1, ..., xn + 1 veszteséges). Ha az utolsó sor negatív tényező, majd végezze el az előző eljárás (az átmenet egy új szimplex tábla) újra. A véges számú lépésben megkapjuk az optimális lúgos oldatot vagy bizonyítja, hogy nincs optimális megoldás.
2. példa a kivitelezési a termékek előállítására az 1. és 2. típusú 10 egység 1. alapanyag és 8 egység a 2. anyag. Minden egyes terméket 1-es típusú fordított 2 egység minden egyes alapanyag és minden egyes termékre 2. típusú töltött 4 és 1 egység minden típusú nyersanyag. Gyártási terv, hogy az összes termék a legmagasabb volt.
Hagyja, hogy a termékek az 1. és 2. típusú termelt x1 és x2 egység, míg a nyersanyag 1-es típusú költik, valamint a nyersanyagok, a 2-es típusú. Szükséges, hogy megtalálják a legnagyobb a funkció nem negatív egész szám értékét az érvelés.
Bemutatjuk kisegítő ismeretlen X3 és X4 (maradék nyers 1. és 2. típus), és szerezzen be egy kanonikus probléma:
Összetétele a kezdeti simplex táblázat: