Lecke - merőleges a vonalat
Rövid leírása a dokumentum:
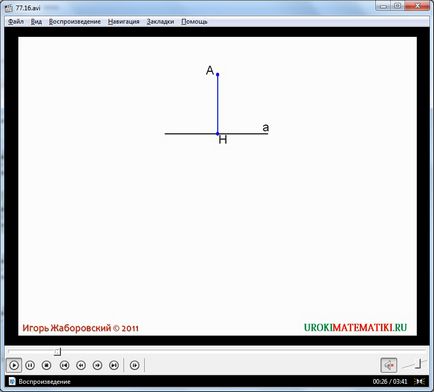
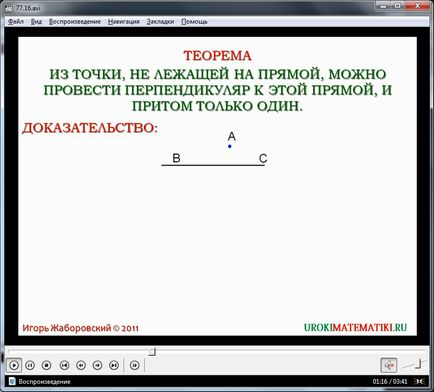
Ezután a diákok úgy tűnik, hogy bizonyítania egy fontos tétel, amely segít megoldani sok geometriai problémák és bizonyítani a következő tétel. A szöveg a tétel megjelenik a képernyőn, és felajánlott egy notebook rögzíteni a diákok. A bizonyíték kezdődik az építkezés a BC egyenest, és pont nem tartozik a közvetlen V Az első bizonyíték - az a tény, hogy a pont lehet merőleges a BC egyenest. Annak bizonyítása, ez az állítás, először épült ∠MVS szög, amely megfelel a szög ∠AVS épült, az elején a nap sugarai. Mivel az adatok szögek egyenlőek, majd impozáns azok azonosak. Továbbá, az ugyanazon az oldalon a BA és BC ∠AVS oldala BM és a nap szöge ∠MVS. Ebben az esetben pont alkalmazzák a pont A1. Meg kell jegyezni, H pontja, amely a metszéspontja egyenes szakaszokból AA1 és BC. Ezt úgy lehet értelmezni, impozáns összecsukható felett rajz egy egyenes vonal BC. Így a kapott építőiparban a szegmens AN, és merőleges a vonalat gerenda NA egy vonalban van a gerenda HA1. Így ∠1 - a szög metszi a szegmens AN, és irányítsa a nap ráhelyezve ∠2 - HA1 szöge metszi a szegmens és a közvetlen Nap A szögek és ∠1 ∠2 szomszédosak. Lehet azzal érvelni, hogy minden sorban ezen szögek, mivel az összege szomszédos szögek 180 °, és mivel a keresztezési szögek vannak kialakítva, az AN merőleges vonal BC. Rendeltetése merőleges vonalak a képernyőn látható egy speciális szimbólum, szentelt emlékezve.
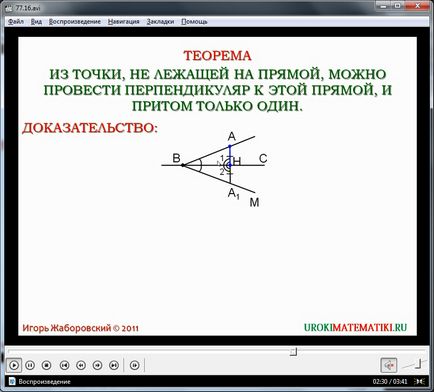
A második rész foglalkozik a bizonyíték arra, hogy a pont lehet végezni egyetlen merőleges a Nap Ez úgy történik, további építési alább az első mintát. A bizonyítás elő az ellenkezőjére. Feltételezzük, hogy az A pont meg lehet tölteni egy pár sort merőleges egyenes V Az ábra, kivéve, merőleges, egy másik vonal csökkent az A pont, hogy a vonal BC. Azonban kiderül, hogy épült egyenes ZH1 metszi a meglévő merőleges Akadémia. De ez lehetetlen, ezért a pont lehet végezni egyetlen egyenes merőleges a nap - ez bizonyítja a tétel.