WolframAlpha orosz, hogyan kell felépíteni egy grafikonon az f (x) alapján a tanulmány eredményeit
Ebben a bejegyzésben, végül össze egy grafikon az eredmények egy korábbi tanulmány.
Egy sor hozzászólás szentelt végrehajtására a közös feladatokat egy változó konstrukció keretében Wolfram | Alpha, mi következetesen tartott több szakaszból áll, meghatalmazotti ha már egy tanulmányt a függvény „kézzel”. Wolfram | Alpha ugyanakkor azt használni, mint egy kiegészítő eszköz - egyfajta számológép minden alkalomra. Ez lehetővé tette számunkra, hogy nagyrészt menekülni rutin számítások, és elsősorban a megfelelő működésének a tanulmány. Anélkül, Wolfram | Alpha néhány szükséges számítások lenne túl időigényes kézi számítások és tanulmány ezt a funkciót úgy tűnik, hogy nekünk túl nehéz.
Ez az a filozófia - a lehetőséget, annak ellenére, mennyisége és bonyolultsága rutin számítások, hogy vizsgálja meg minden olyan funkciót - a fő ok használata mellett Wolfram | Alpha ilyen jellegű problémák megoldását. Tény, hogy az általánosság elvesztése nélkül megoldható elsősorban módszertani feladat -, hogy tanulmányozza és megtanulják, hogyan kell a gyakorlatba átültetni az általános biztosítási rendszer, a kutatási funkciója.
A gyakorlatban azonban, a megoldás az alkalmazott problémák, nem valószínű, hogy bárki menne egy ilyen bonyolult és zavaros módon, kivéve, ha van más lehetőség. És vannak. A megoldása során ezeket a lehetőségeket én szisztematikusan megvizsgálták, és megpróbált összpontosítani rájuk a figyelmet: ez az egyedi igények Wolfram | Alpha, amely lehetővé teszi, hogy „egy kattintással” szükséges, hogy megtalálja az összes egyedi tulajdonságait és jellemző pontjait a funkciót. A részletes bemutatása „hands-on” megközelítés a tanulmány a funkciók segítségével a Wolfram | Alpha, ellentétben az „elméleti”, amely már követte minden alkalommal, bemutatásra kerül az egyik ilyen hozzászólások.
Azonban vissza a végső szakaszban a klasszikus rendszer az átfogó kutatási feladatokat. Ez a negyedik szakaszban a teljes rendszerben a kutatás funkciót. E lépés - Ki kell építeni az eredményeket a fenti tanulmány függvény grafikonját:
A fő feladata a negyedik szakaszban a következők: spolzuya és a korábbi kutatási eredmények építeni egy grafikonon az f (x). Ehhez szükségünk van az eredmények minden korábbi kutatási szakaszok funkciót.
Ez a feladat, különösen az önálló munkavégzésre a diákok, még pontosabban kell meghatározni formájában egyéni feladatok:
16.1. Döntetlen koordinátarendszerben megadott eredmények korábban a domain ezt a funkciót (lásd még a függvény domain Wolfram | Alpha.), És több funkció számértéke (lásd még: több funkció értékek Wolfram | Alpha.). Ez az információ szükséges ebben a szakaszban, hogy felhívja a koordináta-rendszert úgy, hogy a függvény grafikonját található a nagyméretű, és a közepén, és nem a „nagyon magányos kakas” a gyermek szemfelnyitó könyvet Carlson, aki él a tetőn :)
16.2. Jelölje meg azt a pontot az x-tengelyen a diszkontinuitás. Tájékoztatás pontok diszkontinuitás kapunk a vizsgálat domén ezt a funkciót.
16.9. Döntetlen függvény grafikonján az összes jelek és pontok, alkalmazva a rajz alapján. Én nem ezt itt - csak lusta csinálni kézzel (felhívni a grafikon a papírra, majd lefényképezni vagy szkennelni.). Annál is inkább, hogy a következő szakaszban, már megkapta ezt az ütemtervet a Wolfram | Alpha.
17. Vizuálisan ellenőrizze a helyességét a rajzoló funkciókat használja a lekérdezés: plot f (x) x = a..b, ahol [a, b] a szegmenst, amely tartalmazza az összes funkciók jellemző pontok talált korábban:
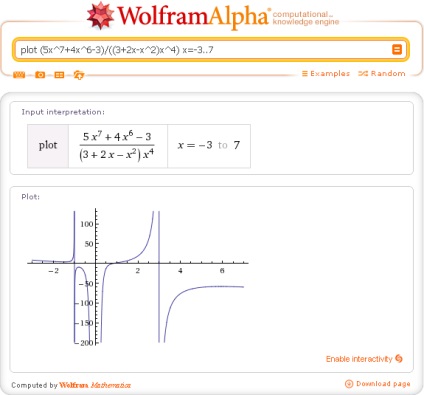
Vagy kérés aszimptotákkal f (x). hogy itt is, mint sok más esetben, ha megjelenik egy még nyilvánvalóbb eredmény:
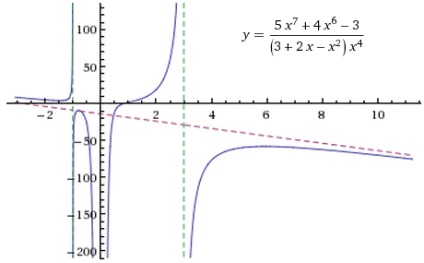
18. A fennmaradó, alkalmazásával kapott ütemezés funkció, elemzi a geometriai tulajdonságainak az épített gráf (szimmetria tengelyével ordinátán, az eredete a koordináta-rendszer, stb), és következtetéseket vonjanak le a tulajdonságok páros-páratlan és a gyakoriságot, a f (x). Ez a rész hagylak független tanulmány.
Ui
Ahogy ígértem az elején ezt a bejegyzést, az egyik ilyen hozzászólásokat lesz ellátni a részletes kimutatás „hands-on” megközelítés a tanulmány a funkciók segítségével a Wolfram | Alpha, ellentétben az „elméleti”, amely már követte minden alkalommal.