vektor termék
Tulajdonságok vektor termék
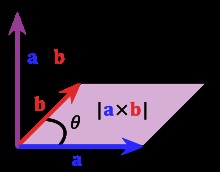
A terület egy paralelogramma egyenlő a vektor termék
- A és b vektorok> kollineáris, ha, és csak akkor, ha a × b = 0 = \ mathbf>. A definíció következik, hogy a eltűnő a kereszt termék egyenértékű vagy egyenlőség nullára az egyik tényező (a nulla vektor kollineáris a többi), vagy eltűnő sine közötti szög a vektorok. Mivel bármilyen vektor kollineáris magában, majd a × a = 0>.
- vektor terméket modul számszerűen egyenlő a terület a paralelogramma kialakított ezen vektorok. Ez következik a meghatározás. Legyen e> - az egység vektor merőleges a vektorok a és b>, és a kiválasztott, hogy a hármas (ab e), \ mathbf)> pozitívan orientált, S Π (a b)) >> -. Területe a paralelogramma épített a vektorok egy, és b>. Ezután a × b = S Π (a. B) e = S _)> \ mathbf>.
- Antikommutativitás: a × b = - b × a = - \ mathbf \ times \ mathbf>.
- Asszociativitás viszonylag skalár szorzata: (K a) × b = k (a × b) = a × (K b) = k (\ mathbf \ alkalommal \ mathbf) = \ mathbf \ alkalommal (k \ mathbf)>.
- Disztributivitás hozzáadásával: (1 + 2) × b = 1 × b + a 2 × b + \ mathbf _) \ alkalommal \ mathbf = \ mathbf _ \ alkalommal \ mathbf + \ mathbf _ \ alkalommal \ mathbf>.
- A Jacobi identitás: (a × b) × c + (b × c) × a + (c × a) × b = 0) \ alkalommal \ mathbf + (\ mathbf \ alkalommal \ mathbf) \ alkalommal \ mathbf + (\ mathbf \ times \ mathbf) \ times \ mathbf = \ mathbf>.
- Lagrange identitás: a × (b × c) = b (a ⋅ c) - c (a ⋅ b) \ alkalommal \ mathbf) = \ mathbf (\ mathbf \ cdot \ mathbf) - \ mathbf (\ mathbf \ cdot \ mathbf )>. Megjegyeznünk a használat emlékeztető „BAC mínusz TSAB»
Vector termék ortonormált koordinátarendszerben szerkesztése
a × b = (a 1 e 1 + a 2 e 2 + 3 e 3) × (b 1 e 1 + b 2 e 2 + b 3 e 3) = = a 1 b 1 e 1 × E 1 + a 2 b 2 e 2 × e 2 + 3 b 3 e 3 × e 3 ⏟ 0 + (a 1 b 2 - a 2 b 1) e 1 × e 2 ⏟ e 3 + (a 1 b 3 - 3 b 1) e 1 × e 3 ⏟ - e 2 + (a 2 b 3 - 3 b 2) e 2 × e 1 3 ⏟ e = = | 2, 3 b 2 b 3 | e 1 - | 1 3 b 1 b 3 | e 2 + | 1 2 b 1 b 2 | e = 3 | 2, 3 b 2 b 3 | e 1 + | 3 3 b 1 b 1 | e 2 + | 1 2 b 1 b 2 | e 3 \ mathbf \ times \ mathbf = (A_ \ mathbf _ + A_ \ mathbf _ + A_ \ mathbf _) \ alkalommal (B_ \ mathbf _ + B_ \ mathbf _ + B_ \ mathbf _) = \\ = \ underbrace B_ \ mathbf _ \ alkalommal \ mathbf _ + a_b_ \ mathbf _ \ alkalommal \ mathbf _ + a_b_ \ mathbf _ \ alkalommal \ mathbf _> _> + (a_b_-a_b _) \ underbrace _ \ alkalommal \ mathbf _> _ _> + (a_b_-a_b _) \ underbrace _ \ alkalommal \ mathbf _> _ _> + (a_b_-a_b _) \ underbrace _ \ alkalommal \ mathbf _> _ _> = \\ = a_a _ \\ b_b_ \ end> \ mathbf _-a_a _ \\ b_b_ \ end> \ mathbf _ + a_a _ \\ b_b_ \ end> \ mathbf _ = a_a _ \\ b_b_ \ end> \ mathbf _ + a_a _ \\ b_b_ \ end> \ mathbf _ + a_a _ \\ b_b_ \ end> \ mathbf _ \ end >>