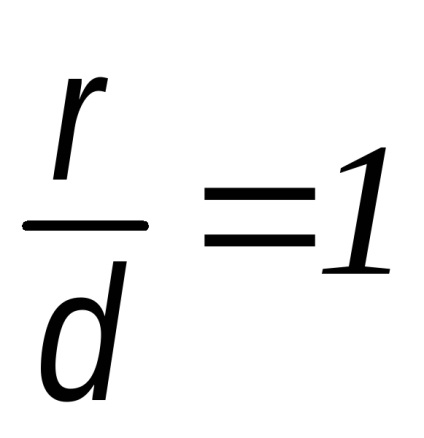Túlzó és kanonikus egyenlete
Definíció. A hiperbola a pályája pont különbség amelyek mindegyike két adatpont nevű gócok állandó
Vegyünk egy koordináta-rendszert, így a hangsúly feküdt az x tengely, valamint a származási megosztott szegmens F1 F2 fele (ábra. 30). Jelöljük F1 F2 = 2c. Ezután F1 (a, 0); F2 (-c; 0)
M
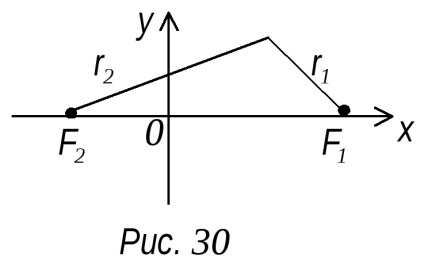
Definíciója szerint egy hiperbola r1 - r2 = const.
Jelöljük ezt a 2a
=> A kanonikus egyenlete a hiperbola
Mivel a hiperbola egyenlete x és y a még hatáskörét, ha a pont M0 (x0, y0) van egy hiperbola, akkor is hazugság M1 (x0, y0) M2 (-x0; y0) M3 (-x0; y0).
Következésképpen, a hiperbola szimmetrikus tekintetében mind a tengely.
Amikor y = 0 x 2 = 2, és X = ± a. Hiperbola csúcsai az A1 (a, 0); A2 (-a, 0).
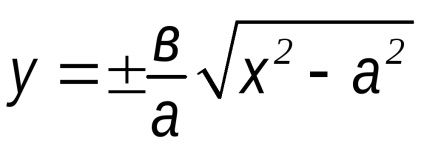
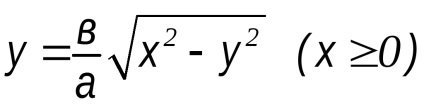
1)
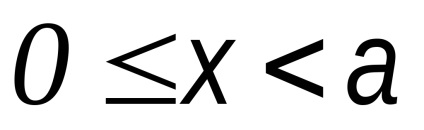
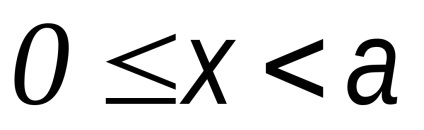
2) x = a; y = 0 A1 (a, 0) tartozik a hiperbola
3) ha X> a; y> 0. Továbbá, alatt korlátlanul szaporodnak hiperbola ág x tart a végtelenbe.
Ebből következik, hogy a hiperbola egy görbe, amely két végtelenített ág.
6. P aszimptotái hiperbola
Vegyük együtt egyenlet
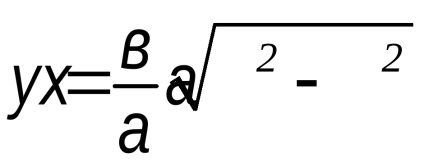
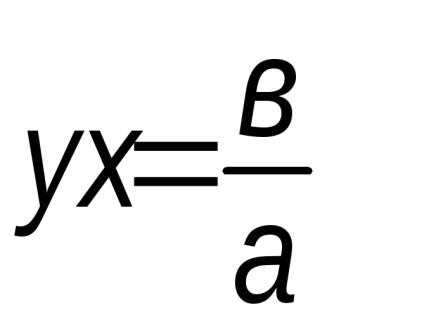
K
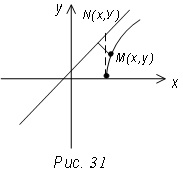
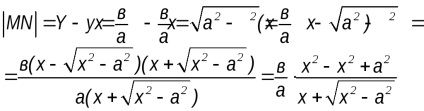
Tehát, ha az M pont, mozgó túlzás az első negyedévben eltávolítjuk a végtelenbe való távolsága a sorban
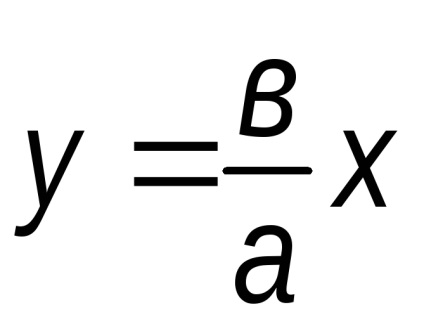
Szimmetria, ugyanez igaz a közvetlen
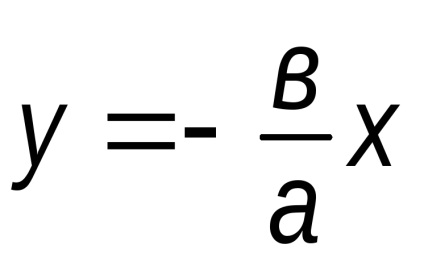
Definíció. Közvetlen, amelyekre az
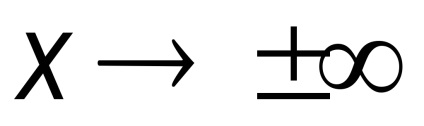
és
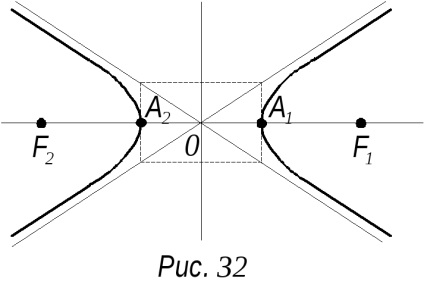
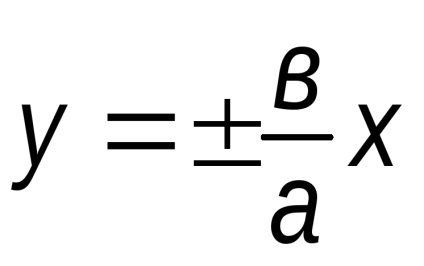
Hiperbola aszimptotákkal mentén vannak elrendezve, az átlók a téglalap, amelynek egyik oldalán van, a tengellyel párhuzamos Ox és egyenlő 2a, míg a másik a tengellyel párhuzamosan Oy és egyenlő a 2c, és a központ a származási (ábra. 32).
N 7. excentricitás és a direktrixszel hiperbola
r2 - r1 = ± 2a + jel utal a jogot a hiperbola ág
mark - utal a bal oldali ága a hiperbola
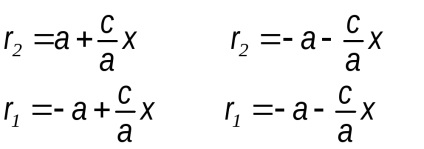
Opredelenie.Ekstsentrisitetom hiperbola az aránya közötti távolság a gócok a hiperbola és a távolság közötti csúcsok.
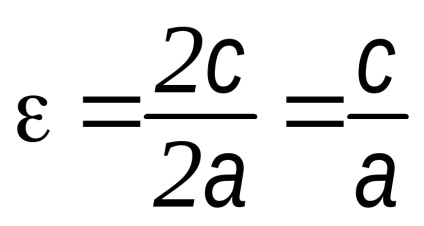
Fejezzük fokális sugarai keresztül túlzás excentricitás:
Definíció. Hívjuk közvetlen
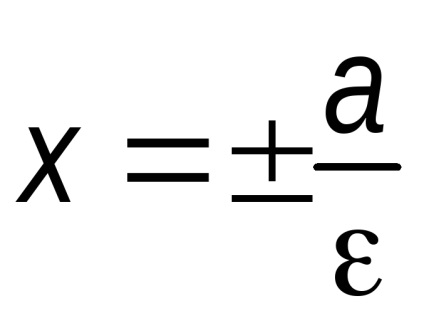

T
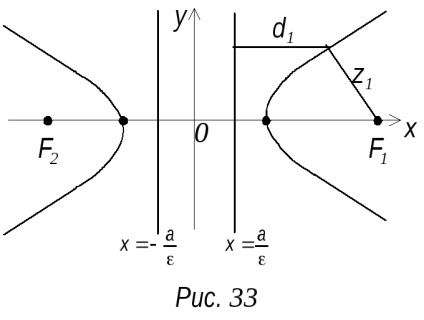
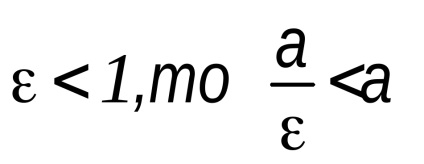
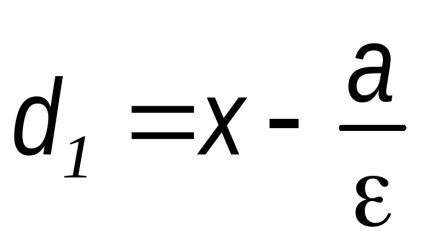
P. 8 parabola és egyenlet
Oh
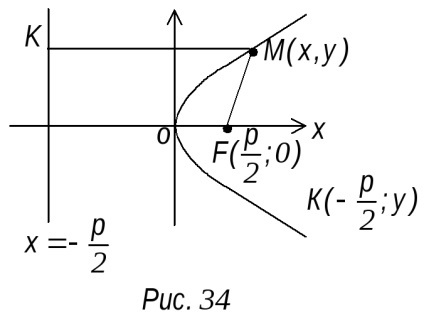
Ahhoz, hogy az egyenlet a parabola vesszük az x-tengely az a vonal fókuszán átmenő F1 merőleges a igazgatónő és feltételezik, hogy az X tengely által irányított igazgatónő összpontosítani. Mivel a származási O veszi a közepén a szegmens a F pont, hogy az adott sorban, melynek hossza jelöli p (ábra. 34). A mennyiség p fogják hívni a paraméter a parabola. fókuszpont koordinátáit
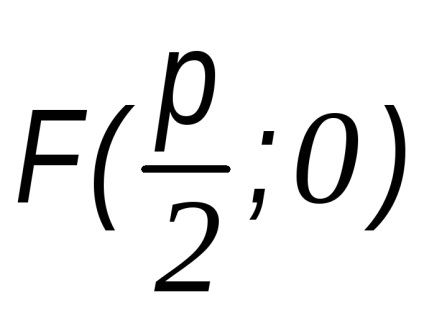
Legyen M (x, y) - tetszőleges pontja a parabola.
v2 = 2px - kanonikus egyenlete parabola
Annak megállapításához, a forma a parabola egyenlete átalakítsa a
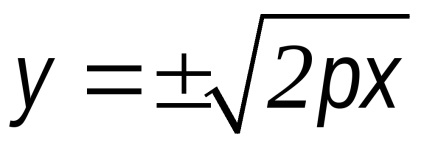
-ban
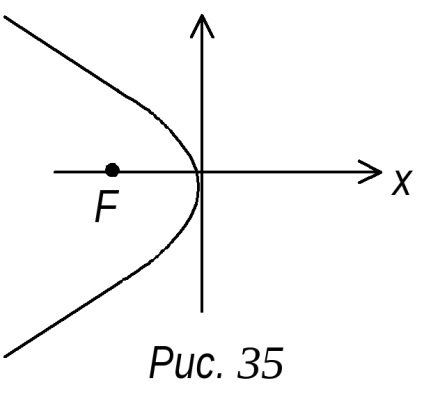
x
Az egyik szimmetriatengelye a parabola.
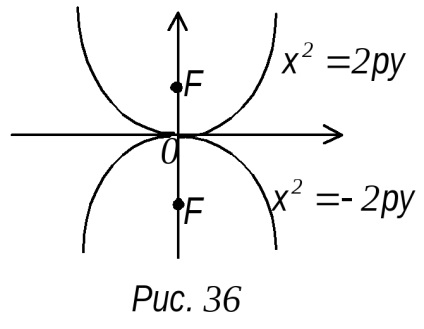
Ha x az első erő és Y a második, azaz a szimmetriatengely X.
Ha x a második fokozatot, és az első, a szimmetria tengely az y-tengely.
Megjegyzés 1.Uravnenie igazgatónő parabola formában van
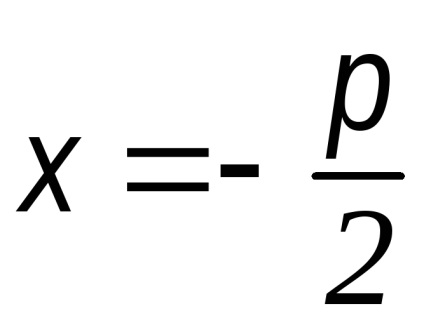
Megjegyzés 2.Tak a parabola