tulajdonságai determinánsok
Kofaktor az elem \ (> \) \ (> \)
A tényleges szám: \ (k \)
Természetes számok: \ (n \), \ (i \), \ (j \), \ (s \)
Meghatározója négyzetes mátrix \ (\ left (>> \ right) \) a sorrendben \ (n \) egy polinomiális álló mátrix elemeinek tartalmazó \ (n! \) Feltételek formájában \ (\ right) ^ s >>>>> \ cdots >> \). Minden ilyen távú egyikének felel meg a \ (n! \) Különböző megrendelt készletek \ (,, \ ldots \), amelyek következtében \ (s \) páronkénti permutációk a több \ (1,2, \ ldots, n \) . Az érték a meghatározó megmarad alatt lineáris kombinációi sorok vagy oszlopok vagy átültetése a mátrix.
A meghatározó n-ed rendű van írva a formájában
A meghatározója a mátrix másodrendű
A meghatározója a másodrendű áll \ (2 \) szempontjából, amelyek mindegyike egy olyan termék a \ (2 \) elemek:
\ (\ Det A = \ left | >>>>> \\ >>>> \ end> \ right | = >>>> \)
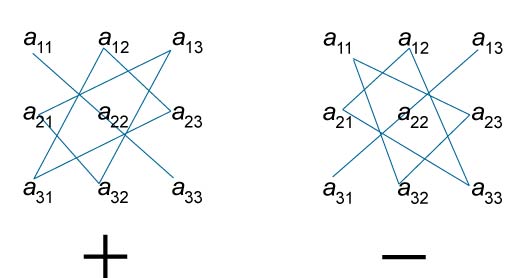
A meghatározója a harmadik rendet, a mátrix is számíthatjuk Sarrusa szabályokat.
Három a hat kifejezések szerepelnek a kulcs a „plusz” és a három - a jel „mínusz”. A mindenkori tripla elem vázlatosan az ábrán látható.
kisebb
További kisebb \ (> \) kapcsolódó elem \ (> \) négyzet mátrixot \ (A \) \ (n \) - edik érdekében az a meghatározó \ (\ left (\ right) \) - edik érdekében megfelelő a mátrix a áthúzott \ (i \) - edik sorban, és \ (j \) - edik oszlop.
kofaktor
Kofaktor \ (> \) kapcsolódó kisebb \ (> \) arány
\ (> = \ Right) ^ >> \)
Laplace-tétel
A determináns n-edrendű lehet segítségével számítható Laplace-formula.
Bomlása meghatározó elemei az i-edik sorban van formájában
\ (\ Det A = \ sum \ limits_ ^ n >>>, \; \; i = 1,2, \ ldots, n \)
Bomlási meghatározó elemek által j-edik oszlop képlete
\ (\ Det A = \ sum \ limits_ ^ n >>>, \; \; J = 1,2, \ ldots, n \)
A determinánsa az átültetett mátrix
Az érték a meghatározó nem változik, ha a sorok és oszlopok a mátrixban cserélhetők (azaz, az átültetési mátrix):
\ (\ Left | >>> \\ >> \ end> \ right | = \ left | >>> \\ >> \ end> \ right | \)
Permutáció sorok és oszlopok a meghatározó
Ha két sorban (vagy két oszlop) felcseréljük a meghatározója a jel változik az ellenkezője:
\ (\ Left | >>> \\ >> \ end> \ right | = - \ left | >>> \\ >> \ end> \ right | \)
A meghatározó az azonos sorok vagy oszlopok
Ha két vonal (vagy két oszlop) meghatározó azonosak, a meghatározó nulla:
\ (\ Left | >>> \\ >> \ end> \ right | = 0 \)
A szorzás a sorban vagy oszlopban állandó determinánst
Szorzás elemek minden sorban (vagy oszlopban) azonos számú egyenértékű megszorozzuk a determináns azt a számot. Más szavakkal, az állandó szorzó elem minden sorban (vagy oszlopban) lehet venni, mint egy jel a meghatározó.
\ (\ Left | >>> \\ >> \ end> \ right | = k \ left | >>> \\ >> \ end> \ right | \)
A lineáris elemek kombinációja a meghatározó
Ha az elemek az egyes sorok (vagy oszlop) hozzáadásához a megfelelő elemeit egy másik sorban (vagy oszlopban), szorozva egy konstans faktorral, az érték a meghatározó nem változik:
\ (\ Left |> + k >> \\ + k >> \ end> \ right | = \ left | >>> \\ >> \ end> \ right | \)