Töltés és kisütés a kondenzátor
A bekapcsolás pillanatában (), a kondenzátor feszültsége nulla (). A bekapcsolás után (állásban „1”) a kondenzátor lemezeket fog felhalmozódni töltés. azaz ott van a kondenzátor töltési folyamatot. A kapocsfeszültsége a kondenzátor arányos a töltés annak lemezek:
A töltés során a kondenzátor egy áramkörben áram folyik:
Következésképpen, a töltőáram a kondenzátor arányos a változási sebességének feszültség a kondenzátor lemezeket.
Tekintsük a folyamat változó a kondenzátor feszültsége és a jelenlegi az áramkörben a töltés közben a kondenzátor, azaz az időszak után, amíg a teljes kondenzátortöltődési mikor. amely megfelel a tranziens folyamat az áramkörben egy kapacitív elemet.
Azonosítani a természet változása kondenzátor feszültsége és a jelenlegi az áramkörben. Alkotunk az egyenlet szerint a 2. törvénye Kirchhoff (1. ábra b):
Behelyettesítve az aktuális értéket a (2) (3):
ellenállás és a kapacitás a termék:
Ez az úgynevezett folyamatos láncot időt és másodpercekben mérjük. majd:
Elválasztó változók, megkapjuk:
Expression (5) egy differenciálegyenlet, amelynek megoldása:
Ez az egyenlet azt mutatja, hogy a kondenzátor feszültsége változik exponenciálisan (növekvő kitevő). Elméletileg kondenzátor (2.ábra) töltési folyamat időtartama végtelenségig, mivel a kondenzátor feszültség egyenlő lesz csak akkor, ha. Gyakorlatilag töltési folyamat befejeződött keresztül (4-5).
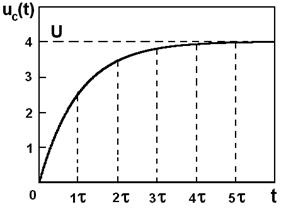
Ettől. amit egyre. A lassabb a kondenzátor töltési folyamat.
Egyenlet (3) tudjuk levezetni azt a kifejezést áram az:
ami azt jelenti, hogy:
Egyenletből (8) következik, hogy a jelenlegi az áramkörben változik csökkenő exponenciális amelynek maximális pillanatában gerjesztési, ettől. és feltöltése után a kondenzátor (3.).
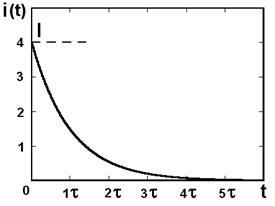
II. Process kondenzátor kisülési
Tekintsük az áramkört, amikor a kapcsoló „1” állásba van állítva a „2”. kondenzátor lemezeket tölteni kezd csökkenni, a jelenlegi a kör lesz, és ezért, a kondenzátor mentesítést. A jelenlegi az áramkörben határozza meg a rothadási sebességét a kondenzátor töltésének lemezeken (amint azt a „-” jel).:
A 2. Kirchhoff-törvény:
Megoldása a differenciálegyenlet (10), kapjuk:
Ettől. majd végül:
Kifejezések (11) és (12) azt mutatják, hogy egy csökkenő exponenciális.
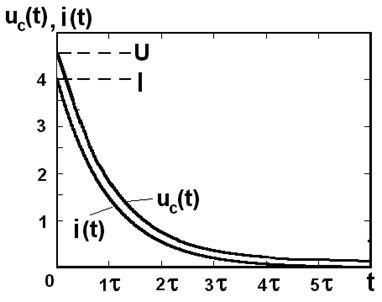
Ábra. 4. ábra feszültség és áram segítségével a kondenzátor alatt kisülés.