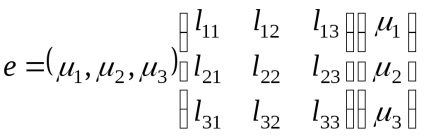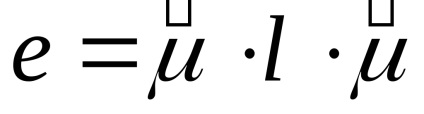Tenzor kis deformációk

Kevesebb kis deformációk jelent mozgása folyamatos közeg, amelyben ez nyúlása a rostok és a relatív kaszálás eredeti szögek közötti szálak sokkal kisebb, mint egy fizikai szálhossz és a szögek között van kis változás. Ezen kívül szükség kevés részleges elmozdulás komponensek képest egységét. Ebben az esetben a kifejezéseket a komponensek a tenzor, a c és E L kis mennyiségben lehet figyelmen kívül hagyni. Így a linearizált deformáció tenzor ilitenzory kis deformációk formában:

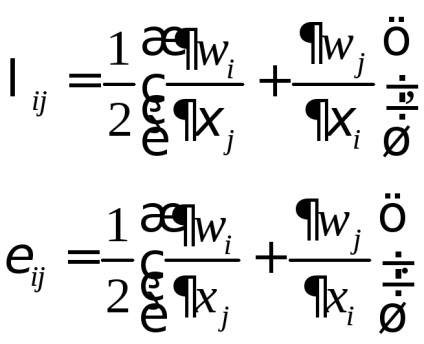
Azt bizonyítja, hogy tenzor kis deformációk ugyanaz.

Példa. Hagyja, hogy a mozgás folyamatos közeg a törvény szerint:

.

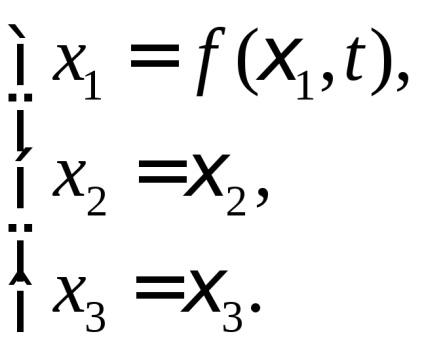
Mi található a tenzor L. Ehhez először kiszámítja a komponensek a elmozdulásvektorból a Lagrange-koordináták:

.

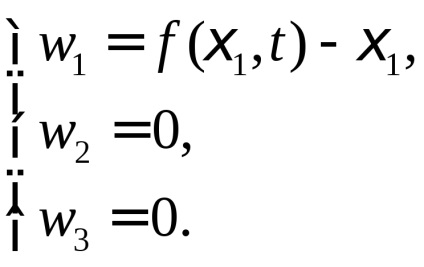
Az összes L nullától összetevői a tenzor lesz egyetlen -

.

.

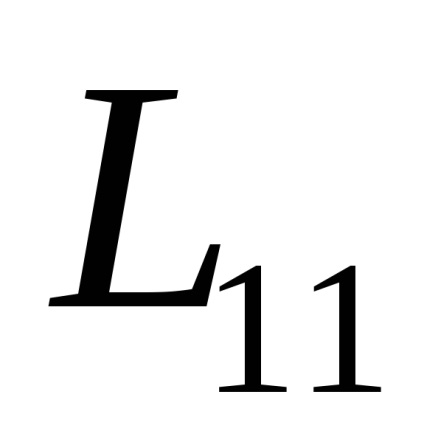
Találunk tenzor E. Először számítsuk ki komponensei elmozdulásvektorból az Euler-koordinátái:

.

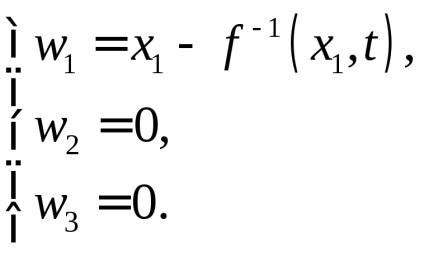
Tenzor E csak egy nulla komponens:

.

.

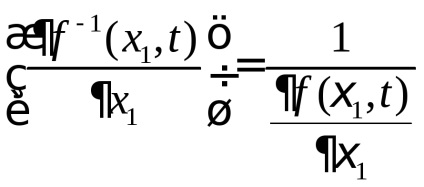
Ezért könnyű megtalálni

A Lagrange-koordináták:

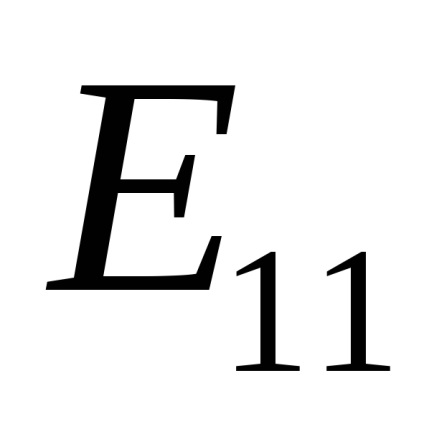
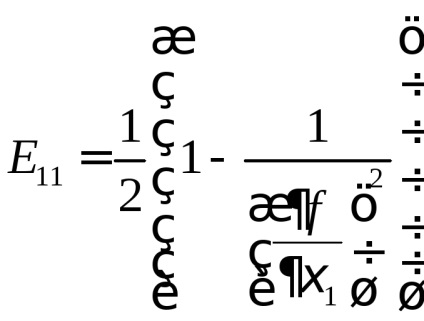
Nyilvánvaló, hogy

. Azaz, az Euler és Lagrange deformáció tenzor nem egyeznek.

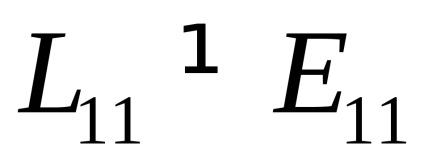
Találunk a Lagrange és Euler tenzor kis deformációk és azt mutatják, hogy azok azonosak.

,

=.

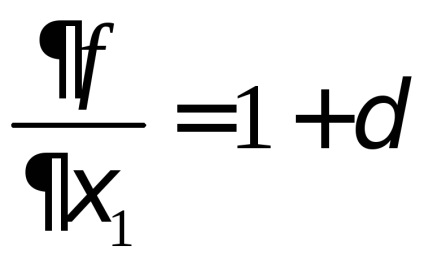
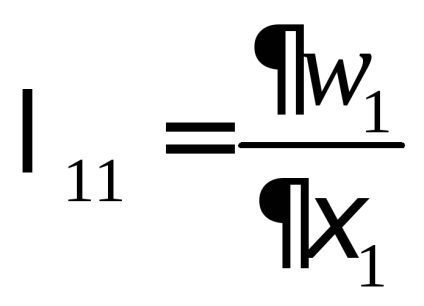
kiszámítjuk

. Mivel a lineáris közelítés

,

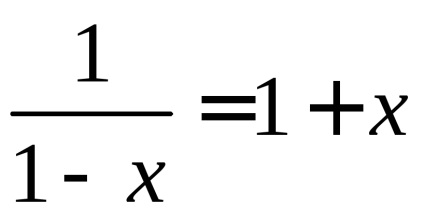
Nézzük most kiszámítani a relatív változás lényeges eleme hosszúságú kis törzsek:

.

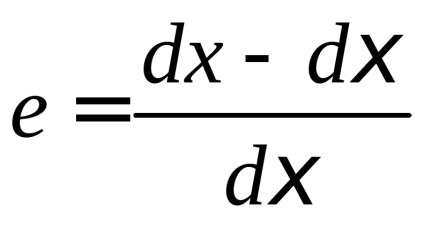
Ebből következik, hogy

.

Mivel a kis mérete a relatív változás a hossza a deformáció kicsi, ezért el lehet hanyagolni a lineáris közelítés a tér ez az érték:

.

.

.

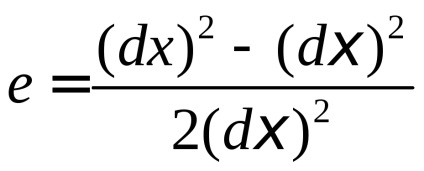
A relatív változása a szegmens hosszát kifejezve a Lagrange vagy Euler tenzor kis deformációk, kapjuk:

,.

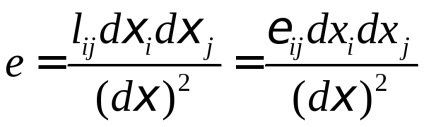
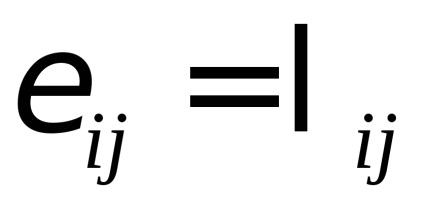
Megadhat egy egységvektor

irányt tekintve a szegmens:

.

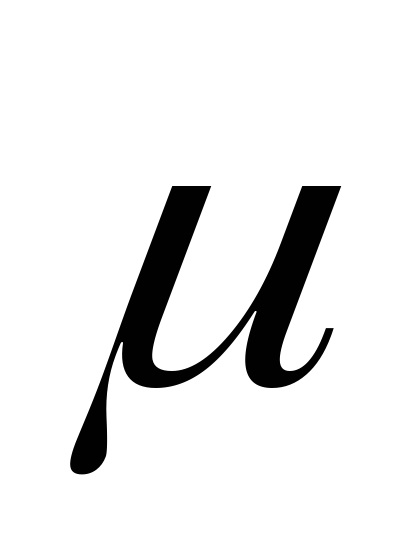
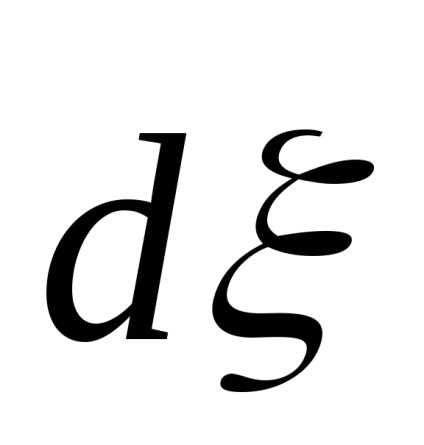
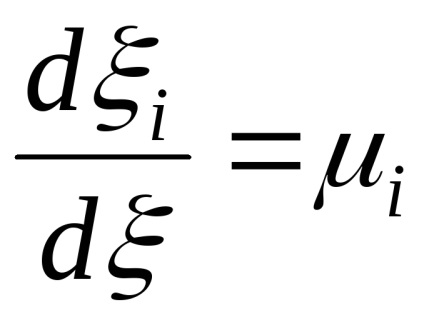
Ezután a képlet

Meg lehet újraírni mátrix formában:

,

.

Mechanikus értelmében a tenzor kis deformációk

Kapcsolódó cikkek

• Strain tenzor - az

• Az elmozdulás a coccyx törzs tünetek, kezelés, következményei

• Compline (rövid) (zajlik szombat este, amikor nincs virrasztás cm