Tapasztalat Stern 1
1. Maxwell törvénye eloszlása a molekulák az ideális gáz sebessége és az energiát.
2. Az ideális gáz Homogén gravitációs mező.
A barometrikus formula. Boltzmann-eloszlás.
3. Az átlagos ütközések számát és az átlagos szabad úthossz a molekulák.
4. Szállítás jelenségek gázokban.
1. Maxwell törvénye forgalmazása molekulák
ideális gáz sebessége és az energia
A gáz egyensúlyi állapotban, a stacionárius eloszlás molekuláris sebességek engedelmeskedve Maxwell törvény.
Clausius
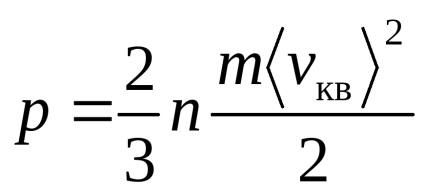
Egyenlet Mengyelejev - Clapeyron



azaz átlagos négyzetes sebessége egyenesen arányos a négyzetgyökével abszolút hőmérséklet a gáz.
Maxwell törvény által leírt f (v), nazyvaemoyfunktsiey a sebesség eloszlás. Ha osztott sor molekuláris sebességeket kis időközönként egyenlő dv. Ezután minden egyes fordulatszám-tartomány figyelembe veszi a molekulák száma dN (v), a ráta ebbe bezárt. A függvény F (v) meghatározza a relatív molekulák számát dN (V) / N, a sebességek a tartományban otv dov + dv. azaz

Módszerek alkalmazásával valószínűségszámítás, Maxwell talált egy f (v) a törvénye eloszlása a molekulák az ideális gáz sebessége:

A relatív molekulák száma dN (V) / N. sebességek a tartományban otv dov + dv. Ez hogyan vetkőzik egy terület ds. A görbe alatti terület az eloszlás és az x-tengely egyenlő eggyel. Ez azt jelenti, hogy az f (V) megfelel a normalizálás feltételt
A legvalószínűbb sebesség skorostyuvv úgynevezett közelében, amely az egység intervallum sebesség a legnagyobb molekulák számát.
Az átlagos sebessége a molekula

A közepes négyzetes sebesség (8)
Tól (6) következik, hogy magasabb hőmérsékleten a maximális molekulák funkció-sebességeloszlás CME-schaetsya jobb (legvalószínűbb értéket-Jat-sósav sebesség nagyobb lesz). Azonban PFSZ - Schad által határolt görbe változatlan marad, így amikor a hőmérséklet emelése görbe a sebességeloszlás a molekulák kifeszített, és csökkentette.
Tengelye mentén a belső henger és a rés kifeszített platina huzal, a cut-edik réteg ezüst, ahol a melegítő-va etsya áram a kiürített levegő. Ha on-Gre-Vania ezüst elpárolog. Silver atomok repül ki a résen, hogy esik rá a belső felülete a második Tsilina-mag, amely a rés képet. Ha a bór-forgásba egy közös henger tengelyére, az ezüst-atomok nem rendezi ellen rés és kiszorítjuk egy bizonyos távolságot. Hasított kapott kép elmosódik. Megvizsgálva a vastagsága a lerakódott réteg, meg lehet becsülni a megoszlása a sebességet, amely megfelel a Maxwell Ras pre-részlege.
2. Az ideális gáz Homogén gravitációs mező. A barometrikus formula. Boltzmann-eloszlás
Ha nem lenne a termikus mozgás, mind a levegő molekulák esne a földre; ha nem lenne gravitáció, a levegő lenne szétszórva az univerzumban. Gravitációs és elmozdulóegységek gáz állapotban, ahol a koncentráció és a nyomás csökken a magassággal.
Kapjuk jogi nyomás változása a magassággal.
A nyomáskülönbség p ip + dp a súlya a gáz zárt a képernyőn henger alap egyenlő területet egység és a magassága dh
p - (p + dp) = g dh

A ideális gáztörvény:

ahol p ir0 - gáznyomás vysotahh és h = 0.
Képletű (12) nevezzük barométer cal. Ebből az következik, hogy a nyomás csökken a magassággal exponenciálisan.
A barometrikus képlet lehetővé teszi, hogy meghatározzuk a h magasság a támogatás egy barométer. Barométer, speciálisan kalibrálni, közvetlen utalás a tengerszint feletti magasságot nazyvayutaltimetrom. Széles körben használják a légi közlekedés, miközben mászni a hegyet.
Általánosítás barometrikus képletű








IN0 ahol n - molekuláris koncentráció vysotahh 0 és h = 0, ill.
1.


2.


3. Az átlagos ütközések számát és az átlagos szabad úthossz a molekulák
A szabad úthossza a molekulák

Tényleges átmérője molekulyd úgynevezett minimális távolság, amelyet az összetartó pontot egy ütközés két molekula.
Hatékony molekulák szakaszban

Az átlagos sebesség a molekuláris mozgását

számlálás




mozgását a más molekulák tekinthető együttható

Behelyettesítve (7,30) a (7.28), megkapjuk az átlagos szabad úthossz
gáz állapotban, ahol
