Szabályok ábrázolási - laboratóriumi gyakorlat
Grafikus ábrázolása információ nagyon hasznos lehet, éppen annak tisztaságát. A grafikon segítségével határozza meg a természet a funkcionális függőség, hogy meghatározzák az értékeket. Táblázatok lehetővé teszi, hogy hasonlítsa össze a kapott eredményeket kísérletileg az elmélettel. A grafikonok könnyű megtalálni a magasságra és a mélypontra, könnyű azonosítani hibák, és így tovább. D.
1. A grafikon épül a papírt, a jelölt rács. Hallgatói gyakorlati működik a legjobban, hogy ábrázoljuk.
2. Meg kell mondani, körülbelül akkora, mint a grafikon: ez nem az határozza meg, hogy mekkora a meglévő darab „grafikon papír”, és a skála. Scale kiválasztott elsősorban véve mérési intervallumok (minden tengely külön-külön be van jelölve).
3. Ha azt tervezi, valamilyen mennyiségi adatok feldolgozása az ütemezésnek megfelelően, az adatokat le kell vonni a „tágas”, az abszolút hiba értékek jelenthet igen jelentős hosszúságú szegmenseket. A hibák ebben az esetben jelenik meg a grafikonok szegmensek metszik kísérleti pont vagy téglalap középpontú kísérleti pontban. Méretük az egyes tengelyek kell felelnie a kiválasztott skála. Ha a hiba az egyik tengely (vagy mindkét tengelyen) túl kicsi, azt feltételezzük, hogy megjelenik a grafikonon a pont méretét.
4. A vízszintes tengelyen az értéke az érv, a függőleges - a függvény értéke. Megkülönböztetni a vonal, akkor lehet, hogy végezzen szilárd, a másik - a szaggatott, a harmadik - a pont-vonal, stb Megengedett kiosztani a különböző színű vonal. Nem szükséges, hogy a tengelyek metszik a származási 0: 0). Az egyes tengelyek csak akkor jelenik meg a mérési intervallumok vizsgált változók.
5. Ha félre „hosszú” tengelye nagy számok, a legjobb tényező, jelezve a rendelési számot, hogy vegye figyelembe írásakor jelöléssel.
6. A részeit a grafikon, ahol vannak olyan jellemzők, mint például a hirtelen változása, görbület, maximális. minimális hajlítási et al. szükséges, hogy a nagyobb adatsűrűség pontot. Annak érdekében, hogy ne hagyja ki ezeket a funkciókat, akkor van értelme, hogy építsenek egy ütemtervet egyszer a kísérlet során.
7. Bizonyos esetekben célszerű használni a funkcionális körét. Ezekben az esetekben a tengelyek feküdt nem a mért értékek és a funkciók ezeket az értékeket.
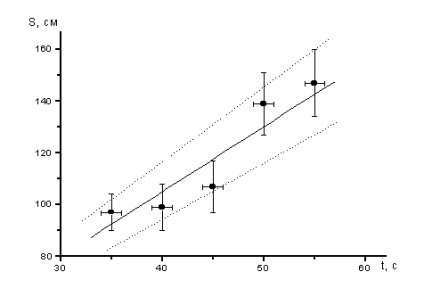
8. Végezze el a vonal „szemmel” keresztül a kísérleti pontokat mindig elég nehéz, a legegyszerűbb esetben, ebben az értelemben, hogy tartsa a vonalat. Ezért, illetve adja meg a sikeres skálán funkció vezethet lineáris összefüggés.
10. A kísérleti pontok általában nem összekapcsolt vagy vonalszakaszok, vagy egy tetszőleges görbét. Ehelyett épített elméleti görbét (lineáris, kvadratikus, exponenciális, trigonometrikus, stb), amely tükrözi nyilvánul ebben a kísérletben ismert vagy feltételezett fizikai mintázat, kifejezve a képlet.
11. A laboratóriumi gyakorlat két esetben: Az elméleti ütemezés célja, hogy kivonat a kísérletben az ismeretlen paramétereket (a vonal meredekségét, a kitevőt, stb), vagy össze lehet hasonlítani előrejelzések kísérleti eredményekkel.
12. Az első esetben a grafikont a megfelelő funkciót végzik „szemmel”, hogy birtokában van minden tartományában hiba a lehető legközelebb a kísérleti pontokat. Vannak matematikai módszerek lehetővé teszik egy elméleti görbe pontokon át egy bizonyos értelemben, a legjobb módja. Végrehajtása során a grafikon „szemmel” ajánlott használni a vizuális értelemben a elmosódása összege pozitív és negatív eltérés a pontokat a görbe követett.
13. A második esetben, a grafikon alapul a számítási eredményeket, a számított értékek nem csak azokat a pontokat, amelyeket úgy kapunk a kísérletben, és egy bizonyos pályán a teljes régió mentén a mérés szerezni egy sima görbe. Rajz a számítások eredményei milliméterpapír formájában pont egy munkapont - miután az elméleti görbét a grafikonon, ezek a pontok távolítani. Ha szerepel a számítási képlet már definiált (vagy előre ismert) kísérleti beállításban, számításokat kell végrehajtani mind az átlagos paraméter értéke és a maximális és a minimális (hibán belül) értékeket. A grafikon ebben az esetben képviseli kapott görbe az átlagos paraméter értéke és a szalag által határolt két számított görbék a paraméter minimális és maximális értékek.