Statisztikai következtetés - 3. oldal
Page 3 4
Most, miután megismerték a statisztikát, mint leírni az adatokat, készek vagyunk, hogy forduljon az adatok értelmezése - hogyan kell levonni belőlük.
Először is, meg kell különböztetni egy csoportot, és a mintát a csoportban. Egyesült Államok Népszámlálási Hivatala megpróbálja leírni a lakosság egészét, beszerezve a leíró anyag életkor, családi állapot, és így tovább. D. Minden ország lakosságának. Szerint a csoport (lakosság) alkalmas a Census Bureau, mivel ez képviseli az összes ember él az Egyesült Államokban.
A statisztikában a „csoport” nem korlátozódik az emberek, állatok vagy tárgyak. Csoport lehet az értéke minden hőmérsékleten, a hőmérő regisztrált az elmúlt évtizedben, minden szó az angol nyelv, vagy bármely más, konkrét adatok raktáron. Sokszor nem férnek hozzá az egész csoportot, majd igyekszünk bemutatni azt a mintát véletlenszerűen vett
(Elfogulatlan) eljárás. Akkor fel bármilyen kérdést egy véletlenszerűen kiválasztott része az emberek, mint ahogy azt a Census Bureau néhány közelmúltbeli népszámlálás; Akkor abból átlaghőmérséklet, eltávolítjuk a hőmérőt egy bizonyos időben, és nem folytat folyamatos felvétel; meg tudjuk becsülni a szavak száma az enciklopédiában, számítva a szavakat egy véletlenszerűen kiválasztott oldalakat. Mindezen példák egy mintát a csoportból. Ha ezen folyamatok bármelyikét ismételjük, az eredmények kissé eltérő annak a ténynek köszönhető, hogy a minta nem tükrözi teljes mértékben a csoport, mint egész, és ezért abból áll mintavételi hiba. Itt van, hogy jön a képbe a statisztikai következtetés.
Minta gyűjtött adatok a csoportból, hogy a következtetés ebben a csoportban. Akkor vizsgálja a mintát a népszámlálási adatok, hogy megtudja, hogy a népesség öregszik, például, hogy van-e a migráció trend a külvárosi területeken. Hasonlóképpen kísérleti eredmények azt is vizsgálták, hogy meghatározzák, milyen hatást gyakorolt a kísérleti manipulációk volt a viselkedése - ha a mennyiség a küszöbén megítélése pályát érinti-e, vagy az oktatás terén különösen jelentős hatással a jövőben az élet. Ahhoz, hogy a statisztikai következtetéseket, szükséges, hogy értékelje a kapcsolat, amely pontnál a minta adatokat. Az ilyen következtetések mindig némi bizonytalanság miatt a mintavételi hiba. Ha a statisztikai vizsgálatok azt mutatják, hogy a hatás nagyságrendje, a mintában talált kellően magas (relatív értékelést a mintavételi hiba), akkor sem lehet biztos, hogy a megfigyelt hatás a mintában létezik a csoport egészére.
Így a statisztikai következtetés az kell levonni, vagy megítélésére néhány jellegzetes csoportok alapján csak a nyert információ mintát ebből a csoportból. Mivel nyúlik a statisztikai következtetés tartjuk normális eloszlás és annak alkalmazását az értelmezés a szórás.
Amikor nagy mennyiségű adatot gyűjtött, táblázatba, és megjelenik hisztogram formában vagy boríték, akkor gyakran hoznak létre egy harang alakú szimmetrikus eloszlását, ismert, mint a normális eloszlás. A legtöbb összetevőjét található, közel a középső (csengő felső pont), és a harang esik meredeken a legnagyobb és a legkisebb érték. Egy ilyen alakú eszköz a görbe különösen érdekes, mert ez történik akkor is, ha a folyamat eredménye alapján halmaza véletlen események, amelyek mindegyike fordul elő egymástól függetlenül. Demonstrációs eszközt ábrán látható. P4, lehetővé teszi, hogy hogyan véletlenszerű események hajtogatott normális eloszlás. Véletlen tényező -, hogy az acél labda esik a bal vagy a jobb minden alkalommal ez lesz a villa - vezet a szimmetrikus eloszlás: több golyó esik kellős közepén, de időről időre az egyik eléri az egyik külső irodák. Ez egy praktikus megjelenítését, mit jelent a véletlenszerű eloszlásban közel normális eloszlást.

Ábra. P4. Berendezés bizonyító normális eloszlás véletlen változó.
Készülék fejjel lefelé, amíg az összes acél golyók nem gördülnek le a tartályba. majd
eszköz fordított, és függőlegesen tartottuk addig, amíg a gyöngyök halad keresztül a területen a csapok nem süllyedni a 9 fészkek alján az oszlopok. A pontos száma golyók kifogott minden egyes oszlopban a különböző tüntetések változik. Ugyanakkor az átlagos magassága az oszlopok golyó fogja ismételni kb normális eloszlás, ha a legmagasabb oszlop lesz a központban, és a magassága a többi hangszóró csökken a szélek felé.
Normál eloszlás (ábra P5.) - egy matematikai ábrázolása idealizált elosztó generált mintegy eszköz ábrán látható. P4. Normál eloszlás azt mutatja, annak a valószínűsége, hogy az elemek a csoportban normális eloszlás különbözni fog az átlagos bármilyen kívánt értékként. Százalékos látható. P5 jelentése egy töredéke a görbe alatti terület között fekvő említett értékek a skála; teljes görbe alatti terület megfelel a csoport egészére. Körülbelül kétharmada minden esetben (68%) tartományba esik közötti plusz és mínusz egy standard eltérés az átlagos (± 1 g); Esetek 95% -ában - az intervallum ± 2G; és szinte minden esetben (99,7%) - ± 3G.
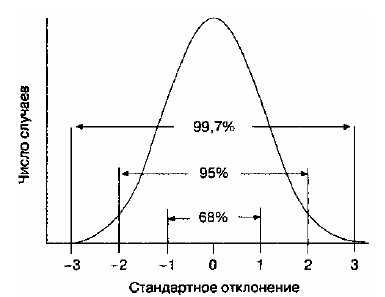
Ábra. P5. Normális eloszlás. meg lehet építeni egy normális eloszlási görbe segítségével szórás és az átlag. A görbe alatti terület, amely abban rejlik, hogy a bal és a jobb oldali 3a + 3a elhanyagolható.
Még részletesebb alatti területek a normál görbe részek táblázatban látható. P4.
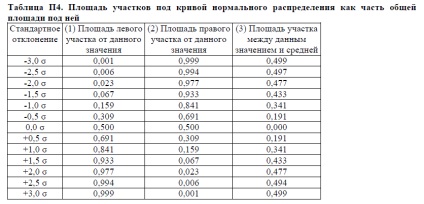
Éljünk a táblázatban. P4 nyoma levezetett értékek 68% és 95% ábrán látható. P5. Táblázat. P4 a harmadik oszlop, azt találjuk, hogy között -1G és az átlag 0,341 és a teljes terület közötti + 1 ° C és átlagosan is 0,341 összterület. Összegezve, ezek az értékek így 0,682 mint látható. P5 jelenik 68%. Hasonlóképpen terület -2o a + 2O 2 x 0,477 = 0,954, látható, mint 95%.
Értelmezni az alak, gyakran kell tudni, hogy magas vagy alacsony az egyéb mutatók. Ha a személy, aki a vezetői vizsgát köteles 0,500 másodpercig nyomja a féket, miután a vészjelzés, hogyan lehet azonosítani, hogy gyorsan vagy lassan? Hiszel abban, hogy egy diák telt természetesen a fizika, ha a rekord a vizsga 60? ez szükséges ahhoz, hogy a skála, amellyel ezeket a paramétereket, hogy válaszoljon ezekre a kérdésekre lehet hasonlítani.
rangsor adatokat. A számok rangot a magas vagy alacsony, akkor kap egy ilyen mérleg. Külön indikátor értelmezhető az a tény, hogy mi pont ő csoportja között mutatók. Például, a diákok a Katonai Akadémia West Point, hogy hol vannak az osztályban - talán 35-bites vagy 125-mi egy osztályban 400.
Normál sebesség. Szórás - kényelmes skáiázóegység, mint tudjuk értékelni, hogy milyen messze az átlagtól helyezkednek 1 ° C vagy 2 ° (A4 táblázat.). Értéke a termék, ahol az egy tényező - szórás, úgynevezett standard intézkedés. Sok mérlegek használt pszichológiai mérések elvén alapuló standard index.
Példa a kiszámítására a standard index. Táblázat. P1 mutatja a kapott számokat 15 diák a felvételi vizsgák. Anélkül, hogy több információt, azt nem tudjuk, hogy ezek a számok a csoportot reprezentáló valamennyi kérelmező. Azonban, feltételezzük, hogy a medián E vizsgálatokat 75, és a szórása 10.
Mi lesz a szokásos intézkedés egy diák, aki szerzett 90 pont a vizsgák? Hogyan átlag feletti ez a szám kell kifejezni száma szórások:

Ebben az esetben a hallgató komponens alatt fekszik átlagosan 2,2 szórások. Így a jele a normál érték (+ vagy -) azt jelzi, hogy nagyobb vagy kisebb az átlagos mutató aktív, és az ár-érték azt jelzi, hogy messze van az átlagos egységekben szórások.
Hogyan reprezentatív átlag?
Milyen jól működik az átlagos minta tükrözi az átlagos az egész csoport? Ha megmérjük a növekedés véletlenszerűen kiválasztott 100 főiskolai hallgató, milyen jól minta átlaga jósolja az igazi, a csoport átlagával (azaz az átlagos növekedés minden főiskolások)? Ezek mind kapcsolatos kérdéseket a következtetést a csoport alapján minta adatokat.
A pontosság ez a következtetés függ a mintavételi hiba. Tegyük fel, hogy nem két véletlen minta ugyanabból a csoportból, és ezek mindegyikére kiszámítja az átlagot. Mi a különbség az egyik és a másik közeg következtében várható az ügy?
Későbbi véletlenszerű mintát ugyanabból a csoportból fog adni a különböző közeg, amely egy eloszlása mintaközegnek körül igaz, a csoport átlagával. Ezek mintaátlagokat magukat azok az értékek, amelyekre lehet számítani a szórást. Ez egy szórás nevű standard hiba az átlag; ez jelöli Sm és számítjuk a következő képlet segítségével:
ahol egy - szórása a minta, és az N - az esetek száma, amelyek az átlagos kerül számításra.
E szerint a képlet, az átlagos érték standard hiba csökken a növekvő mintanagyság; így az átlagos alapuló nagyobb mintán sokkal megbízhatóbb (valószínűleg közelebb lesz az igazi átlaga az egész csoport). Ez várható volt, alapján a józan ész. SEM világosan mutatja, hogyan bizonytalan a kapott átlag. Minél nagyobb a minta mérete, annál kisebb a bizonytalanság a közeg.
Sok pszichológiai kísérletek, az adatgyűjtés két csoport alanyainak; az egyik csoport van kitéve egy adott kísérleti hatásokat, és a másik kontrollként szolgál. A kérdés az, hogy van-e különbség az átlagok között ezek a csoportok, és ha igen, hogy az megmaradjon az egész csoport, amelyből a két mintát vettünk. Egyszerűen fogalmazva, ha a különbség a két csoport között tükrözi a valódi különbség, vagy merült miatt a mintavételi hiba.
Példaként összehasonlítani a teljesítményét teszt olvasás minta aránya malchikov- első osztályosok az első osztályosok a mintavevő és a lányok. Mivel az átlagos, de alacsonyabb, mint a fiúk, de van jelentős átfedés; néhány fiú megbirkózni kivételesen jól, és néhány, a lányok - nagyon rossz. Ezért nem tudjuk elfogadni ezt a különbséget közegben lefolytatása nélkül a statisztikai szignifikancia. Csak akkor tudjuk eldönteni, hogy az tükrözze a megfigyelt különbségek a mintában az igazi különbség a csoport vagy ezek magyarázzák a mintavételi hiba. Ha néhány a több tehetséges lányok és néhány, a buta fiúk véletlenszerűen kiválasztott, a különbség azzal magyarázható, a mintavételi hiba.
Egy másik példa, tegyük fel, hogy az általunk végzett kísérletben, mint egy erőd kézfogás férfiak jobbkezes és lefties. A felső részén a táblázat. P5 mutatja hipotetikus adatok ebben a kísérletben. A mintát 5 handers férfiak átlagosan 8 kg erősebb mintát 5 férfi handers. Mi általában következtetni lehet ezeket az adatokat a férfiak lefties és jobbkezes? Mondhatjuk, hogy a jobb kezes az erősebb? Nyilvánvalóan nem, hiszen a kapott átlag a legtöbb jobbkezesek, nem lenne más, mint az átlag a legtöbb balkezesek; Egy említésre méltó jellemző indikátor értéke azt jelzi, hogy 100 van dolgunk bizonytalan helyzetet.
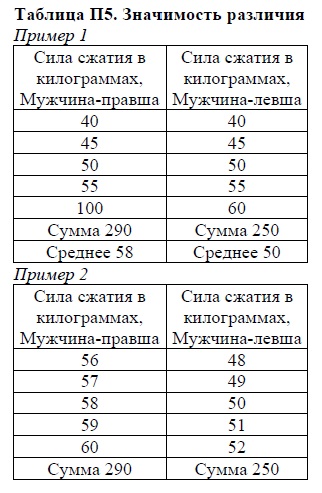
Most tegyük fel, hogy ennek eredményeként a kísérlet eredményeit, látható az alján a ugyanabban a táblázatban. P5. Ismét azt látjuk ugyanazt közötti különbség átlagosan 8 kg, de most ez az információ inkább hiteles, mivel a mutatók a balkezes emberek is kiderült, hogy rendszeresen alacsonyabb, mint a jobbkezesek. Statisztika lehetővé teszi, hogy pontosan figyelembe venni a megbízhatósága az átlagos különbség, hogy a meghatározását, amely a két különbség sokkal megbízhatóbb, nem csak attól függ, intuíció.
Ezek a példák azt mutatják, hogy a jelentősége a kapott eltérések függ a nagysága és változékonysága az összehasonlított átlagok. Ismerve a standard eltérés az átlagtól, akkor lehet számítani a standard hibája a különbség a két eszköz ODM. Ezután, a kapott különbséget lehet segítségével becsült kritikus viszonyt - egy kapcsolat származó átlagos különbség (DM) a standard hiba az átlaga közötti különbség:
Ez lehetővé teszi, hogy értékelje a jelentőségét különbség a két átlag. Mint egy egyszerű szabály, hogy a kritikai attitűd nem lehet kevesebb, mint 2,0 az átlagos különbség szignifikánsnak tekinthető. A könyvben a kifejezés a „statisztikailag szignifikáns” kifejezés azt jelenti, hogy a különbség a kritika őket, hogy legalább.
Miért a statisztikailag szignifikáns kiválasztott kritikus arányban, 2,0? Csak azért, mert egy ilyen nagy értékű, vagy leeshet véletlenül csak 5% -ában. Hol volt az 5% -os? Kritikus hozzáállás lehet tekinteni, mint egy standard mértékegység, mert ez csak a különbség két átlag kifejezett számának standard hiba. Hivatkozva a 2. oszlopban adtuk. P4, vegye figyelembe, hogy annak a valószínűsége, hogy a szórás 2,0 esetén a véletlen egybeesés egyenlő 0,023. Mivel a valószínűsége eltérése az ellenkező irányban is egyenlő 0,023, a általános valószínűség 0,046. Ez azt jelenti, hogy ha az átlagos csoportok azonosak, a kritikus arány véletlenül egyenlő 2,0 (vagy több) 46 esetből 1000, vagy 5% -ában.
Elementary általánosságban elmondható, hogy a kritikus arány nem lehet kevesebb, mint 2,0, azaz olyan - tetszőleges, de kényelmes szabály, amely meghatározza az 5% -os szignifikancia szinten. Követve ezt a szabályt, a valószínűsége a hibás döntések, hogy az átlagos különbség van, holott ez nem lesz kevesebb, mint 5%. Nem feltétlenül, hogy egy 5% -os szinten; Egyes kísérletek esetében nagyobb jelentőséggel bír, attól függően, hogy mennyi hiba elfogadható következtetésre.
Számítási példa a kritikus arány. A számítás a kritikus kapcsolatok meghatározásához szükséges standard hibája a különbség a két átlag az alábbiak szerint:
Ebben a képletben OM1 és OM2 - standard hiba képest két átlag.
Illusztrációként tegyük fel, hogy mi kell összehasonlítani az eredményeket első osztályosok - fiúk és lányok a vizsga az Egyesült Államokban olvasni. Vegyünk egy véletlen minta fiúk és a lányok a vizsgálat alatt. Tegyük fel, hogy átlagosan 70 fiú standard eltérés az átlagtól 0,40 és a medián lányok - 72 a standard hiba az átlagtól való eltérés 0.30. Alapján ezeket a mintákat kell dönteni, hogy van-e valódi különbség a sikeres fiúk és lányok olvasni a csoport egészének, adat mintavétel azt mutatják, hogy a becslések a lányok, mint a fiúk, de lehet következtetni arra, hogy mi lenne, hogy ugyanazt a vizsgálatával az összes amerikai első osztályosok? Problémák lehetővé teszi a kritikus hozzáállás.
Mivel a kritikus lényegesen magasabb arány 2,0, azt lehet mondani, hogy a mért átlagos különbség statisztikailag szignifikáns 5% -os szinten. Ezért arra lehet következtetni, hogy van egy megbízható különbség az olvasás fejlődése között fiúk és lányok. Megjegyezzük, hogy a kritikus arány lehet pozitív vagy negatív, attól függően, hogy milyen átlagos levonásra; a kritikus hozzáállás értelmezését figyelembe véve csak a nagyságát, de nem a jel.