Solid fizika
1. kristályrács
1.1.Klassifikatsiya kristályrétegeiben
A kristályrács - egy térbeli hálózat, ahol a csomópontok vannak elrendezve részecskék (atomok, molekulák, ionok) alkotó kristályok.
A kristályrács alapul elemi kristályos sejt - paralelepipedon egy jellemző Ez az elrendezés a rács atomok.
O. French kristályosító Bravais alakult 1848-ban a geometriai elmélete kristályszerkezet, attól függően, hogy a relatív nagysága és relatív orientációját az egység kristályrács a bordák, van 14 típusú kristályrétegeiben (Bravais rács).
P
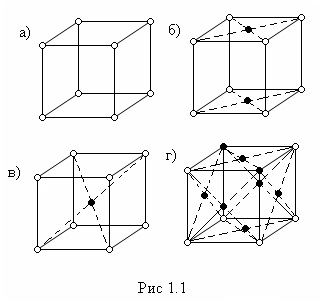
Ha a rács helyek vannak elrendezve csak a csúcsok egy paralelepipedon elemi hálószemek, a rács nevezett primitív (egyszerű) (ris.1.1.a); ha ezen felül, vannak olyan helyek a közepén a doboz bázisok - bázis-központú (ris.1.1.b); ha vannak csomópontok metszéspontjában a test átlók - egy tércentrált (ris.1.1.v); ha vannak csomópontok közepén az arc - az arc-központú (ris.1.1.g).
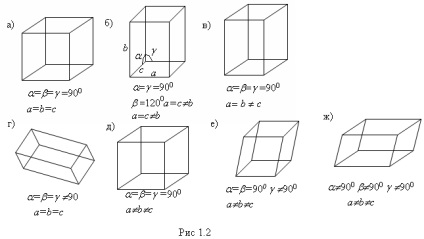


Egy komplex kristályszerkezete leírható mint egy gyűjtemény a kis Bravais rácsok, betoljuk egymással.
Elhelyezkedés részecskék kristályrácspontjaiban egyaránt az egész kristályt. Az amorf szilárd anyagok és folyadékok zajlik legközelebbi rendelést elrendezése részecskék tekintetében bármely részén a helyét a legközelebbi szomszédok rendelik, mivel ugyanez a távolság a részecske helyét vele kapcsolatban más részecskék kevésbé rendezett.
1.2. A szimmetria a kristályok
A természetben, gyakran szemben a kristályok a megfelelő külső formát formájában poliéder, amelyben egyenértékű arcok és élek periodikusan ismétlődő, azaz a kristály szimmetriája.
Symmetry a jelenlétére utal a tárgyak valami változatlan, invariáns, tekintettel bizonyos átalakításokat. A szimmetria geometriai formák - az ingatlan tartalmaznak egyenlő és egyenletesen elrendezett alkatrészek. Forgatás körül bármelyik tengelyére, a reflexió egy ponton, vagy síkidom kombinálni lehet önmagában. Ezek a műveletek nevezzük szimmetrikus transzformációk, és geometriai kép jellemzésére különböző szimmetrikus transzformációját - szimmetria elem. Minden egyes darab legalább egy pont, amely a helyén marad, amikor a szimmetrikus transzformációját. Ebben az értelemben a kristályok egy pont szimmetria. A kristályok száma szimmetria elemeinek korlátozott megkülönböztetni tükör szimmetria sík, forgási szimmetria tengelye (közvetlen és tükrözött), egy középső szimmetria vagy központja inverzió.
Tükörszimmetriával sík az közvetlenül tükrözi a síkban, mint egy tükör. Ez a sík osztja a testet két egyenlő részre, hogy egybeesik egymással minden Megfontolásra ebben a síkban.
Közvetlen rotációs szimmetriatengelye - egy egyenes vonal, amikor fordult kerülete körül amelynek aránya egyenlő 1 / n. ahol n - sorrendben a tengelye az ábra kombináljuk magát minden ponton. Így a jelenléte ábrán hatszorosára tengely (n = 6) forgási 60 0. Amellett, hogy közvetlen forgócsapok megkülönböztetni még tükör-forgástengely, amelyek egyesítik egyidejűleg befolyásolja a forgási tengelye körül a kerülete aránya 1 / n, és tükröződik merőleges síkban.
A központ a szimmetria, vagy központ inverzió, - egy szinguláris pont az ábrán, a reflexió, amely ábrán egybeesik önmagában, azaz az inverziós művelet során reflexió az ábrán a ponton szám után kapott tükrözi a visszavert és fordított.
A kristályokat találunk csak öt szimmetriatengelye különböző rendű (első, második, harmadik, negyedik és hatodik). A tengely az ötödik, hetedik és magasabb rendű kristályokat csakúgy, mint létezésük nem kompatibilis az elképzelést, hogy a kristályrács.
A teljes készlet szimmetria jellemző elemeket szimmetria objektum osztály nevezett szimmetria. BERENDEZÉSEK 32 osztály kristályszimmetriában.
A térrácshéj szimmetria újabb elemmel - Webközvetítés

Az akció a csúszó a reflexió síkja reflexió csökken a referenciapont egy síkban (mint egy tükör), és ezzel egyidejűleg át mentén sík által összeg felének a fordítást 1 / 2T párhuzamos síkban.
Műveletek csavar tengely csökkenti, hogy forgástengelye körül a referenciapontot a kerülete aránya egyenlő 1 / n. ahol n - a sorrendben a tengely és egy egyidejű mozgatására a tengelye mentén a T / N. elfordulása 360 0 vezet elmozdulásnak a referenciapont tengely mentén egyenlő távolság T adás.
Csavaros tengely lehet a második, harmadik, negyedik, hatodik és megrendelések. A helikális tengelye az első érdekében egyenértékű egyszerű helyettesítési (fordítás).
Ott 230 térbeli szimmetria csoport mindegyike egyedi módon oszlik el a 32 osztályt pont szimmetria. Az átmenet a tér csoport szimmetria osztály kell minden szimmetria elemei a tér csoport, hogy végezzen egy ponton keresztül, és feltételezik, menetes tengely elfordítható tengelyei azonos nevű, és a csúszó a gondolkodási síkon - tükröt.