Részletek a mechanikai rezgések harmonikus
Az egyenletek (1) vagy (2) a legnagyobb elmozdulása az inga az egyensúlyi helyzetből a pozíció az úgynevezett elmozdulási amplitúdóval (xmax). Az SI rendszer a maga egység - mérő:
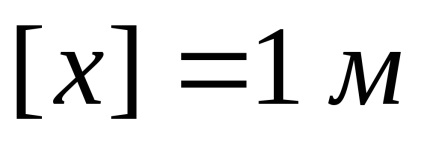
A kifejezést a zárójelben az egyenletek (1) vagy (2) az úgynevezett oszcilláció fázis
Az egység radián fázis:
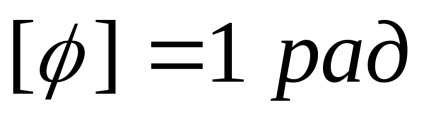
Kezdő időpontjában (Start mozgás) fázis
,
Ezért 0 nevű értéket a kezdeti szakaszban. Meg lehet venni, mint egyenlő 0.
A mennyiség nevezett gyűrűs (vagy szögletes) rezgési frekvencia. Ez radiánban másodpercenként:
.
Ennek során annak értéke nem változik a rezgés. nagysága kapcsolatos nagyságát . úgynevezett rezgési frekvencia, a képlet:
Következésképpen, figyelemmel a (4) képletű, (3) kifejezés a fázis és a oszcillációs törvény (1) formájában, illetve:
A definíció szerint chastotaravna chislaNpolnyh relatív rezgések készült vremyat, ebben az időben:
Ezt az értéket a hertz:
.
A fizikai jelentése a frekvencia az, hogy számszerűen száma egyenlő a teljes rezgések egységnyi idő, t. E. 1 másodpercig
.
Value megegyezik az idő rezgések képest rezgések száma nazyvayutperiodomkolebany
Az időszak másodpercekben mérhető:
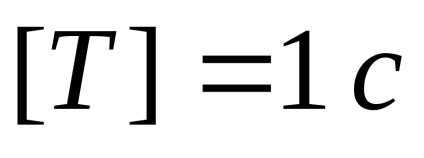
A fizikai jelentése időszak az, hogy számszerűen megegyezik az idő egy teljes lengés
.
Következésképpen, az időszak társított frekvencia és ciklikus gyakorisága a képletek:
Így, tekintettel a képletekben (8), (3) kifejezés a fázis és a oszcillációs törvény (1) formájában:
Mechanikai energia harmonikus rezgések
Az energia a mechanikai rezgések összegével egyenlő a potenciális energia és a mozgási energia:
Energiát mérjük joule:
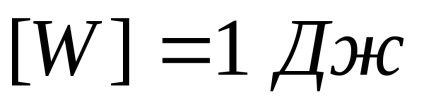
A potenciális energia inga tömeg arányos a tér a rezgési frekvencia, a négyzeten koordináták (offset) egyenlő az inga és a
Behelyettesítve (10) egyenlet oszcilláció jog (1), majd
Nyilvánvaló, hogy a potenciális energia periodikusan változik az időben. Az az időszak, a tér a koszinusz 2-szer kisebb, mint az időszak a koszinusz, ezért a változás időszakát potenciális energia kevesebb, mint 2-szer az időszakban a koordinátákat változik. Egy teljes oszcilláció az inga helyzeti energia kétszer nullává válik, amikor az inga áthalad az egyensúlyi helyzet, és kétszer a maximális érték a maximális elmozdulás az inga.
A maximális érték a potenciális energia
A kinetikus energia arányos az inga tömege és a tér a rezgési sebesség:
A sebesség változás aránya megegyezik a koordinátáit az időben ezt a változást:
sebességegységek - méter per másodperc:
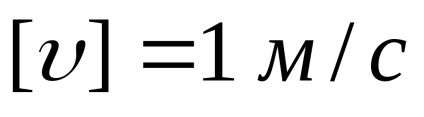
Behelyettesítve (1) egyenlet az expressziót (14), kapjuk:
.
Az amplitúdó a sebesség ingadozások
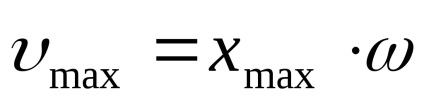
Egy expressziós a sebesség négyzet vozvedom és behelyettesítve (13) egyenlet:
Következésképpen az érték a mozgási energia is periodikusan változtatja az időben, és egy teljes lengés potenciális energia kétszer nullává válik, amikor az inga tolódik, amennyire csak lehetséges, és kétszer van egy maximális értéke az egyensúlyi helyzet az inga.
A maximális érték a kinetikus energia ugyanaz, mint a lehetséges, ha nincs energiaveszteség.
Most azt látjuk, a teljes mechanikai energia az inga helyett kifejezések (11) és (15) a (9) egyenletből:
Így, időtartama alatt a oszcilláció, a teljes mechanikai energia az inga állandó, és egyenlő a amplitúdója a kinetikus és potenciális energiája.