Problémák megoldása a szinusz és koszinusz különbség érvek 4
Ebben a leckében megtanuljuk, hogyan kell megoldani a problémákat a sinus és cosinus az érvelés különbség
Vizsgálata képletek a szinusz és koszinusz érv különbség
Írunk a 2. képlet:
- a koszinusza a különbség az érvek:
,
vagyis a koszinusz különbségének érvek - az összege termékek koszinuszok és szinusz ezeket az érveket.
- sine különbség érvek:
,
.. Azaz a szinusz argumentum különbség - a különbség a termékek a szinusz és koszinusz α β α koszinusz és szinusz β.
A problémák fontos megérteni, hogy a hozott α és β.
1. feladat, hogy egyszerűsítse a kifejezést, amelyet a képlet szinusz érv különbség
1. célkitűzés Egyszerűbb.
5x elfogadott α, r. F. 5xα, és 3xβ, és használja a képlet sine különbsége érveket.
2. feladat, hogy egyszerűsítse a kifejezés a következő képlet segítségével a koszinusz érv különbség
2. Egyszerűbb a feladat.
Alkalmas képlet koszinusz a különbség az érvek, de van egy különbség a termékek, így átalakítsa a kifejezést használva tulajdonát paritás koszinusz függvény és a szinusz függvény tulajdonát oddness:
=
==
Mi a nem csak egyszerűsíteni a kifejezést, hanem annak kiszámításához.
3. feladat, hogy egyszerűsítse a kifejezést, amelyet a képlet szinusz érv különbség
Feladat 3.Uprostit kifejezés.
=
Az ingatlan a paritás funkciók koszinusz és szinusz függvény páratlan ingatlan, megkapjuk:
==
=
==
===
=
Elágazás számítási feladatok a leckét
Számítási feladatok a leckét
Képlet segítségével különbség koszinusz érveket.
Használata képletű különbség sine érv.
==
Vegyünk egy bonyolultabb feladat.
4. feladat találni a szinusz és a számok összehasonlításával képlet segítségével a sinus és cosinus érv különbség
a) Tekintsük a trigonometrikus kört (1. ábra):
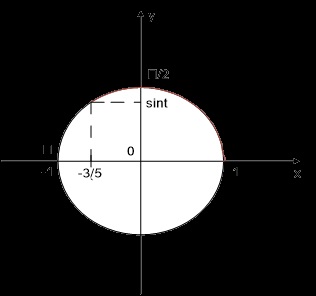
Ábra. 1. A trigonometrikus kör
T jelentése egész szám, ívhossz.
Minden mennyiségben kromenam ismert.
======
Hiányzó szám található.
==
b) összehasonlítása segítséget, ha ez negatív, a szám a második negyedévben, ha pozitív - az első (jobbra a (2. ábra).
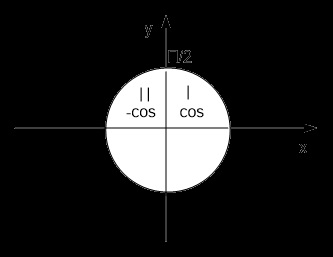
Ábra. 2. Ábra A probléma
Minden mennyiségben ismertek minket:
==
=
Ez egy negatív érték, tehát negatív és koszinusz (található, a második negyed):
Néha meg kell használni a két képlet egyszerre egy feladatot.
Probléma 5 a egyenlet megoldása a képletek a sinus és cosinus érv különbség
Alkalmazzuk a tulajdonságait páros és páratlan függvények a sinus és cosinus furcsa tulajdonság:
==
Kapunk egy egyszerű trigonometrikus egyenlet.
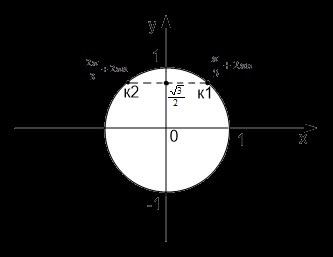
Ábra. 3. ábra A probléma
A szög, t = x + 45pervoe oldatot beállított ad pont k1 (), egy második sokaságát
megoldások - k2 () (3. ábra).
Úgy döntöttünk, hogy megtalálja az egyenletet, és minden döntést, ők számtalan.
Formula sinus és cosinus különbség érvek és megoldani a tipikus probléma ezekkel a képletekkel vizsgáltuk ebben a leckében.
További ajánlott linkek internetes források
Mesék van gyermeke :)))
A szerkesztők most IAMX helyszínen együttműködni tehetséges ember Ekaterina Danilova az ő csodálatos projekt „Tales of a gyermek” az oldalon „asztrológus tipp”. Ezek Könyvek- „Tales” hozható létre Kate és a nap hőse, felnőttek, és minden jelentős családi események, mint például esküvők vagy őt évfordulóját. Egy oldal a „Tippek asztrológus” hangsúlyozni egyéniség és az eredetiség, mint egy emlékezetes ajándék, mint egy „könyv-meséje”. Részletes információk ezek a könyvek megtalálhatók oldalakon vk.com/skazki_pro_vashego_rebjonka és vk.com/ekaterina.veduschaya példa „oldalon asztrológus” egy könyvet a gyermek:

ez érdekes
Kapcsolat
Van még kérdése? Mondja el nekünk, és mi válaszolunk Önnek a lehető leghamarabb.
Egyedi infotainment portált IAMX
A Súgó
AstroWay.In.Ua - hasznos asztrológiai konzultáció
Bejelentkezés Facebook
Belépés a hitelesítő adatok
Elfelejtett jelszó?
Bejelentkezés Facebook