Pénzügyi matematika (4 feladatok)
A hitel 63 TR kiadott 4 évig. A várható inflációs ráta 14% reálhozamráta a művelet legyen 9% -a komplex kamatláb. Határozzuk meg a kamatláb a kölcsön, figyelembe véve az inflációt, a törlesztés összege és a felhalmozott kamat.
1) Az első rész a probléma megoldja két módja van:
a) A számítás a fogadás fog az I általános képletű Fisher:
Ezért, hogy kompenzálja a veszteségeket az infláció miatt, és biztosítsa a nyereségesség szinten 9% pa (kamatos) kell telepíteni névleges sebességével azonos 24.26% -os bruttó.
b) számítása a százalékos arány alapján becsült általános képletű:
Egy évre, m = 1 és n = 1.
Ezért, hogy ebben az esetben a 2 általános képletű értékeinek m és n kapjuk:
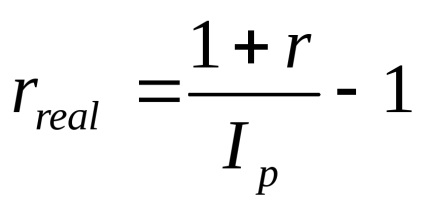
2) kiszámítja az összeget felhalmozott képlet szerint:
Inflációval korrigált, a bank kap:
Ezek közül az adósság törlesztés összege lesz:
Így csak az infláció miatt az adósság nőtt:
106,404.49 - 63.000 = 43,404.49 rubelt.
A felhalmozott kamatot, inflációval korrigált lesz:
150,198.62 - 63.000 = 87,198.62 rubelt.
A valóságban a bank kap jövedelmet csak az összeg:
150,198.62 - 106,404.49 = 43,794.13 rubelt.
Válasz: az infláció:
mértéke lesz 24.26%;
az adósság visszafizetése 106,404.49 rubelt.;
felhalmozott kamat (jövedelem a bank) lesz: 43,794.13 rubelt.
Ez hitelt az összeg 18,0 ezer. Dörzsöljük. Egy 6 hónapos időszakra 24% -os évi havi törlesztés. Visszafizetés történik havi részletekben. Legyen a kölcsön törlesztési terv egységes fizetési fő.
A probléma az állítás nem meghatározott típusú hitel és a módszer a kamatot. Ebben az esetben a hitelező lesz nyereséges, hogy jóváírja „Consumer Credit” (egyszerű kamat), mert A hitel futamideje kevesebb, mint egy éve.
1) Tegyük fel, hogy a kamatszámítás végzik a fennmaradó tartozást.
Az érték a jogvesztő fizetés két részből áll:
A) kifizetése fő (ő állandó a feltétellel, hogy a 18.000 rubel. / 6 hónap. = 3000 rubelt).
B) a visszafizetés felhalmozott kamatot (ebben az esetben azt feltételeztük, hogy a kamatfizetési kötelezettség terheli az egyensúlyt a tartozás). Ezért a felhalmozódott kamat értéke lejárat lesz egyenlő:
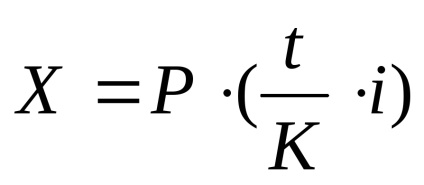
ahol
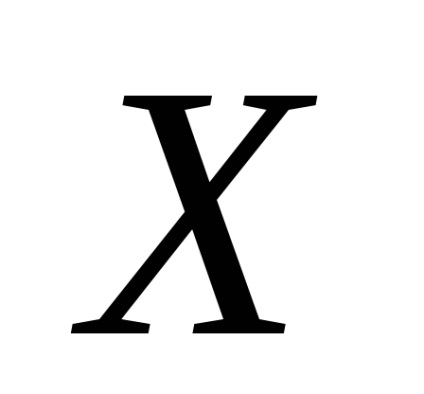
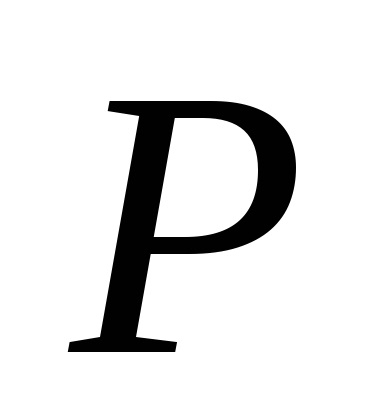
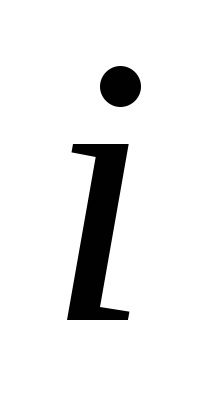
t - a napok számát a művelet (ebben az esetben 30 nap);
K - időalap (360 nap).
Az első felhalmozódott kamat kifizetését lesz: dörzsölje.
A második fizetési felhalmozott kamat lesz: dörzsölje.
felhalmozott kamat összegét a harmadik fizetés: dörzsölni.
felhalmozott kamat összegét a negyedik részlet: dörzsölje.
Az ötödik fizetési felhalmozott kamat lesz: dörzsölje.
felhalmozott kamat összegét a hatodik részlet: dörzsölje.
fizetési terv a következő:
2) Tegyük fel, hogy a felhalmozódott kamatot a teljes tartozás egyszerre, akkor a logikai hitelezési hitelező megpróbálja mivel jövedelmük (felhalmozott kamatot), ezért az áramlás a kifizetések fizeti ki a felhalmozott kamat a lehető leghamarabb eltávolítani egyenletesen csökken. Elkészítéséért tervet jogvesztő kifizetések ésszerűbb, hogy a „78. cikk”, bár akkor bármilyen csökkenő sorrendben frakciók, amíg azok összege egyenlő 1.
Az elején számítani frakciói:
A) számú hónappal összeget kell 0,5 év:
B) frakciókat az alábbiak szerint:
Az első fizetés:
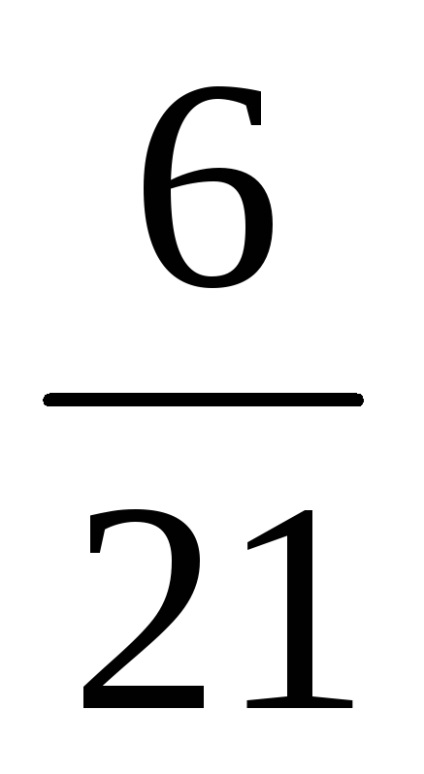
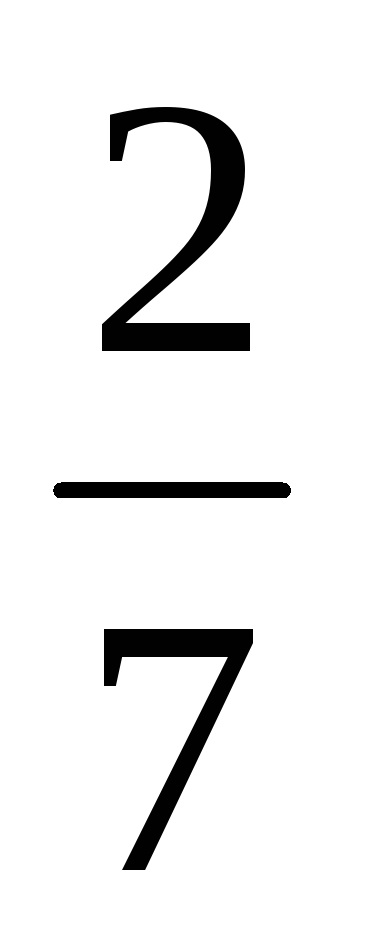
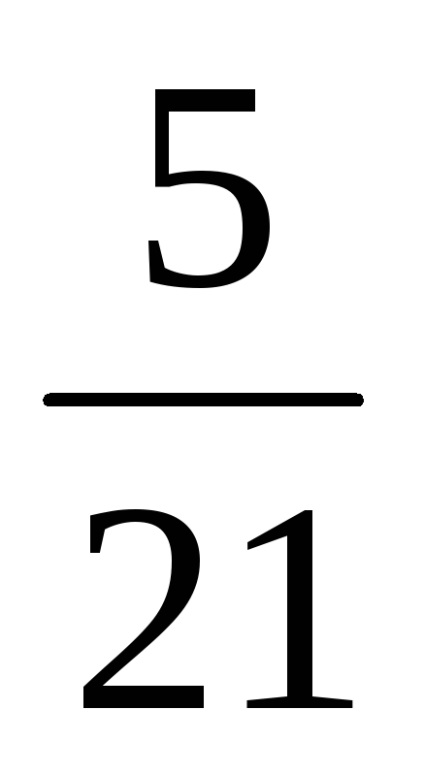
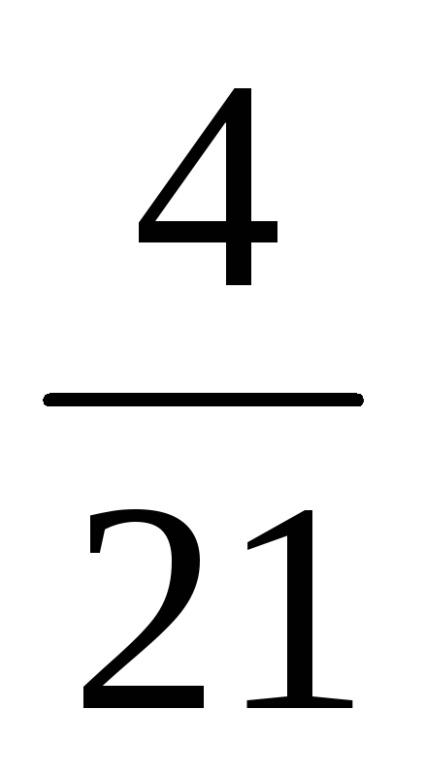
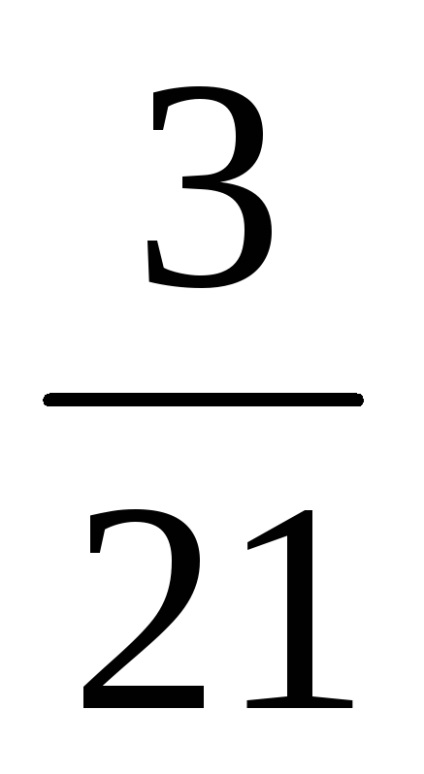
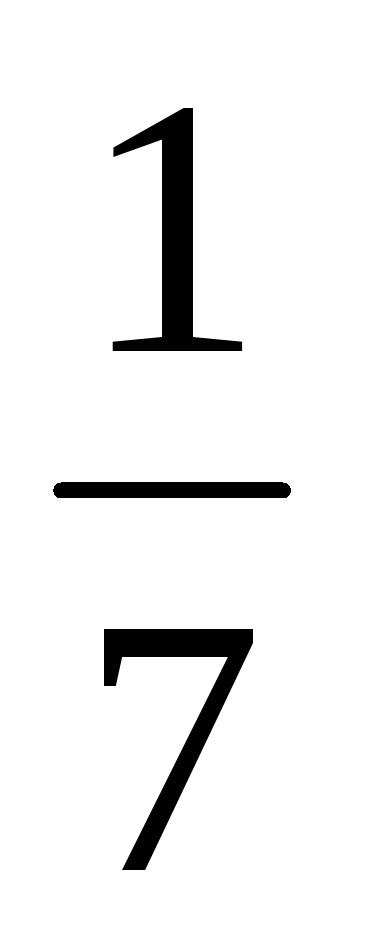
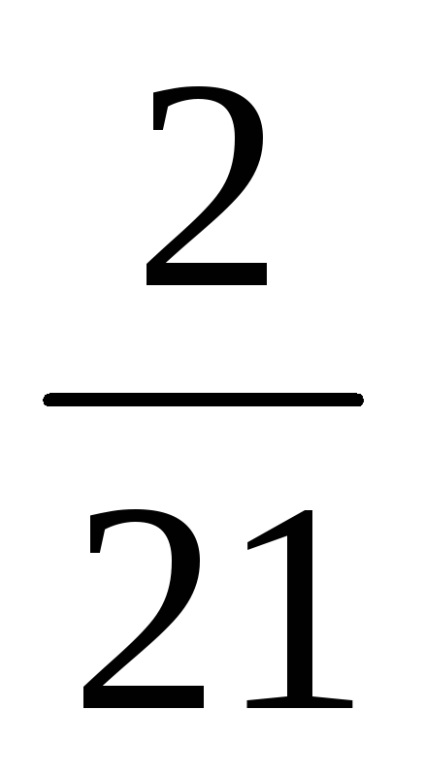
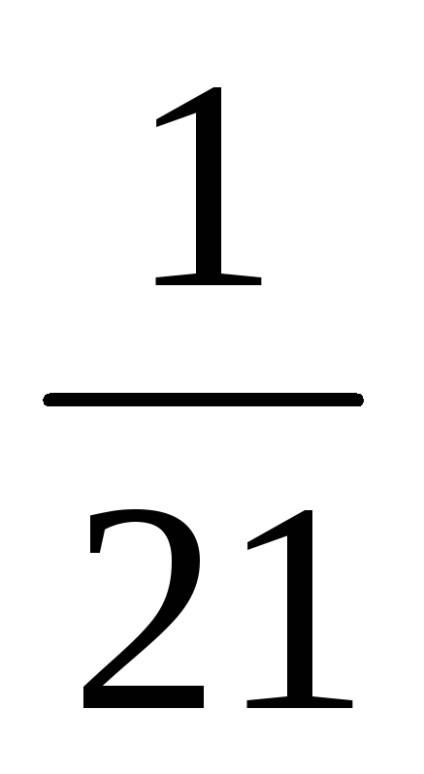
Kiszámítjuk a felhalmozódott kamat összegét:
Most szorozzuk meg az összeg a felhalmozott kamat a mindenkori fizetési frakció, megkapja az összeg visszafizetését az érdeklődés.
Egyenleg a kezdő időpontja
Az érték a tőkeösszeg
A maradékot a az időszak végén
Bank hitelek nyújtása során az 1 év 6 hónap alkalmazott mértéke 25% -kal, a kamat kerül felszámolásra félévente. Értékének meghatározásához egy egyszerű kamatláb, amely biztosítja a bank, egyenértékű összeget.
Backfilled összege egyenlő lesz:
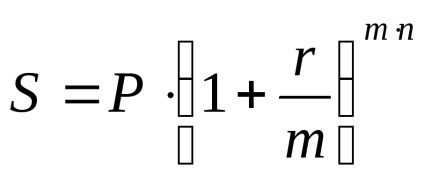
Backfilled összeg egy egyszerű diszkontráta lesz egyenlő:
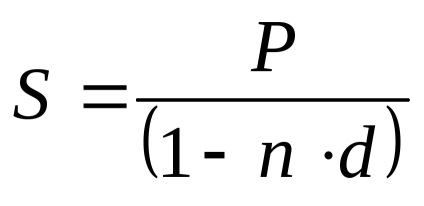
Hitel összege 1 millió. Dörzsöljük. éves kamatos az arány 20% -os évi vissza kell fizetni, egyenlő határozott idejű fizetendő, beleértve a hitel visszafizetését tőke és kamat évente a minden év végén 5 évig. Határozza meg a teljes költség a hitel visszafizetését, és a felhalmozott kamatot.
Sőt, úgy véljük, két változatban fizetés:
A) Az egyszeri tőketörlesztés és a felhalmozott kamat 5 éves korig:
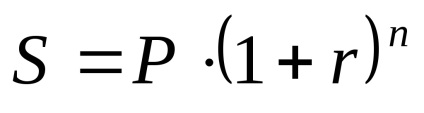
Ha tehát leállítjuk hitelt egy összegben 5 év után, hogy fizetne 2,488,320.00 rubelt.
B) Mi azonban meghívást eloltani a tartozás egyenlő részletekben végén az év. Ezután, a képlet mennyiségének meghatározására egy közönséges életjáradék Felhalmozott (postnumerando), hogy az érték a fizetési lesz egyenlő:
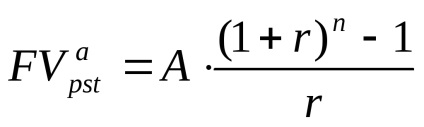
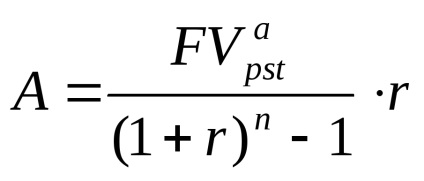
Így az éves egyenlő fizetések összege 334,379.70 rubelt.
Következésképpen, a teljes költség lenne: 334,379.70 rubelt. × 5 = 1.671.898,50 RUB. Ezek közül az érdeklődés: 1,671,898.50 rubelt. - 1000000 rubelt. = 671,898.50 rubelt.
Egy vizuális reprezentációja a teljes költség a hitel visszafizetését és a felhalmozott kamat a betét könyv alkalmazható módszer: