Parabola és annak tulajdonságait, órák és előadások algebra, a 8. évfolyam
Srácok, ne felejtsük hetedikben, és a grafikon a „parabola”. Ahogy emlékszem, az egyenlet egy parabola: $ y = x ^ 2 = 1 * x ^ 2 $.
És mi történik, ha helyettesíteni bármilyen más valós szám a készülék helyett? Nézzük meg a két funkciót: $ y = 2x ^ 2 $ és $ y = 0,5 * x ^ 2 $.
Létrehoztunk egy táblázatot az értékek az egyes funkciókat. Kezdjük $ y = 2x ^ 2 $.
A függvény $ y = 0,5 * x ^ 2 $. Figyelembe véve a megfelelő pontot a koordináta sík és egy összekötő vonal őket, megkapjuk a következő grafikonok.
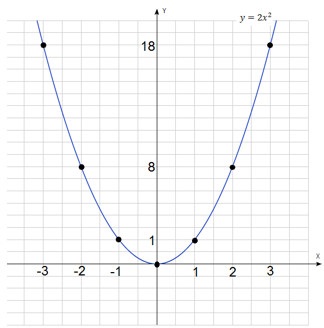
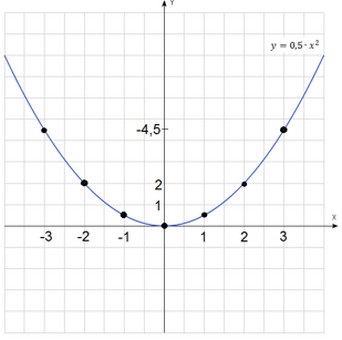
Mindkét diagramok hasonlóak egymáshoz. Nézzük felhívni őket egy koordinátarendszerben, és megtalálja hasonlóságokat és különbségeket.
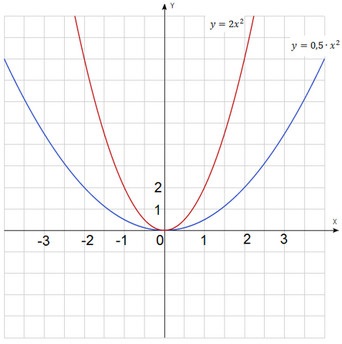
Mindegyik grafikonok nevezzük parabola. A pont koordinátái (0, 0) az úgynevezett parabola csúcsa. OY tengely - a szimmetria tengelye a parabola. Mindkét grafikon felfelé mutat, vagy más szavakkal azt mondja, hogy „a szarvak a parabola” keresi fel. A grafikonok a parabola, le tudjuk írni az egyenletet: $ y = kx ^ 2 $.
De ez a két grafikon vannak különbségek. One - szélesebb, mint a másik, és arra törekszik, ki lassabban, mint az első. Ez egy parabola sebesség különbözik. Minél nagyobb a hányados $ k $, annál gyorsabb a parabola keresi fel, vagy hogy egyre keskenyebb (az OY tengely van nyomva). Minél kisebb a hányados $ k $, annál lassabb a parabola keresi fel vagy szélesebb lesz (távolodik a tengely OY).
Általános esetben a grafikont a parabola $ y = kx ^ 2 $, $ k> 0 $ van felépítve ugyanúgy. Kezdetnek, akkor lehet építeni egy táblázatot az értékek, és vegye figyelembe az összes pont után csatlakozott hozzájuk a görbét. De a parabola csúcsa van a származás, az ágak felfelé, míg a y tengely a szimmetria tengelye a parabola.
És mi történik, ha a parabola együttható $ k $ 0. Branch a parabola lefelé, ha a $ k $ 0. Az egyértelműség kedvéért, itt át az egyik grafikonok épített korábban.

Tulajdonságok a függvény $ y = kx ^ 2 $, $ k> 0 $
1. terület meghatározása. Mi lehet számítani az értékét a függvény bármely ponton x. Ezután a függvény definíciója a $ hε (-∞; + ∞) $.
2. $ y = 0 $ a $ x = 0 $, $ y> 0 $ a $ x ≠ 0 $. Ez a tulajdonság nyilvánvaló és jól látható a grafikonon.
3. A folytonos függvény. Menetrend elhalad a folytonos vonal, a pontok, ahol a függvény nem törött.
4. A legnagyobb érték nem. Az ütemterv szerint azt mutatja, hogy a funkció végtelenül megy fel.
A legkisebb értéke $ y = 0, ha a $ $ $ x = 0. Ahhoz, hogy megtalálja a minimális érték legyen a grafikonon, hogy megtalálja a legalacsonyabb pontja. Ez az a pont koordinátái $ (0; 0) $.
5. A funkció növeli, ha $ x> 0 $. Funkció csökken $ x $ 0.
6. A funkció határolja fent közvetlen $ y = 0 $.
7. Az értékek függvényében: $ (- ∞; 0] $.
8. A függvény konvex felfelé.