Online kalkulátor, hogy meghatározza a csoportok száma hisztogram

Ma beszélünk statisztika, ki fogom fejteni a hisztogram. Általánosságban elmondható, hogy a hisztogram a grafikus kijelző eljárás csoportosulás, azaz a megoszlása ​​a méréssorozat valamilyen mennyiséget csoportok, összhangban egy lényeges jellemzője az ebben a csoportban. csoportosító módszerek széles körben használják feldolgozásra a nyers adatok.

Az elsődleges adatok a statisztikai megértjük a statisztikai sorozat, amely az úgynevezett sorok hangszórók. ha beszélünk változik a jelenség az idő, vagy a forgalmazás sorok. amikor összetételében vagy szerkezetében a vizsgált jelenség.

Mikor jön a soraiban alapuló minőségi jellemzőit (például a vállalkozás által tulajdon), ez a sorozat az úgynevezett jelzős. ha a sorozat által épített változók (például a kockázati forgalom volumene), ezek az úgynevezett variációs.

Attól függően, hogy a folyamatos változását változó megkülönböztetni diszkrét és intervallum variáció sorozat.

A hisztogram egy oszlopdiagram épített az adatokból, amelyeket osztva csoportokra. Az adatok száma a csoporthoz tartozó minden egyes (frekvencia) van kifejezve a magassága a megfelelő oszlopba ebben a csoportban.

A hisztogram lehet építeni bármilyen sorozat, azzal jellemezve, ha ez egy attribútum vagy diszkrét variációs számú (például az alkalmazottak száma az egyes díjszabási kategóriában), a szám a kiosztott csoportok számával megegyező értékek ezzel a tulajdonsággal. Abban az esetben, egy rendezett sorozata intervallum csoportok száma attól függ, hogy az érték intervallum használt csoportosítja az adatokat.

Interval - a különbség a maximális és minimális értékek a tulajdonság minden egyes csoportban. Nyilvánvaló, hogy minél nagyobb a csoport, annál kisebb az intervallum, és fordítva. Csoport ilyen esetben is nevezik az osztály időközönként.

Például akkor tönkreteheti az adatokat a dolgozók száma a következő vállalatcsoportok:
25 fő befogadására alkalmas,
25-50 ember
50-100 fő,
Több mint 100 ember.

Ezután a hisztogram tartalmaz 4 oszlop, amelynek magassága megfelel majd a vállalatok száma fogott ebben a csoportban.
Mellesleg megjegyezzük, hogy a fenti példát eloszlása ​​egyenlőtlen időközönként. dedikált, mint mondják, a kutatási programot, azaz a. e. magunkat.

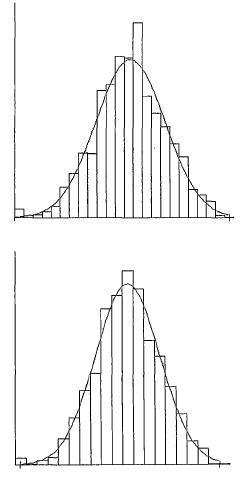
Q érték kiválasztás intervallumot (a csoportok száma) használt csoport megrendelt tételek sorozat intervallum, nem tétlen. Amellett, hogy a hisztogram egy kiváló eszköz az adatok megjelenítés, az is legfeljebb egy közelítése a valószínűségi eloszlásfüggvény (lásd. A képen). E. Az érték az egyes csoportok az oszlop azt mutatja, a valószínűsége, hogy a következő a mérendő tartoznak ebbe a csoportba.

Túl sok csoport adhat túl „ideges” menetrend túl kevés - túl „sima”. Ideális esetben, természetesen, nem lenne kívánatos egy olyan csoportok száma, ami a legkisebb eltérés a valószínűségi eloszlásfüggvény, azaz a. E. Lehetővé teszi, hogy a legpontosabb becslést ez a valószínűség eloszlás függvények a jelenség vizsgált.

Általában ezek a matematikusok nem.

Az első, úgy tűnik, volt Sterdzhesc (Sturges, 1926). Őt tartják az idealizált gyakorisági hisztogramot a k osztályok, ahol az i-edik érték megegyezik a binomiális együttható. Elég nagy k hisztogram alakja megközelíti az alakja normális eloszlást. Az értékek összegével egyenlő
.

Így az N mérési eredmények, amelyek engedelmeskedik normális eloszlás, az osztályok száma használt hisztogram kell venni, mint az alak a hisztogram kapott fog közelíteni az alak a normális eloszlás egy elég nagy k. Ez a képlet Sturgess. Ebben a formában kapott szinte minden tankönyv statisztika.

Ez a képlet most kritizálták csak a tény, hogy kifejezetten használ a binomiális eloszlás közelítése normális eloszlás, ami nem mindig alkalmazható. Úgy véljük, hogy ez a képlet lehetővé teszi, hogy egy kielégítő hisztogram, amely legalább 200 mérés.

Számos alternatív formulák, amelyek közül néhány számított hosszának az intervallum, majd meghatározzuk a számát szükséges osztályok (lásd. A leírásban).

Vegyünk egy pár ilyen formulák:

Formula Scott (Scott, 1979)
, ahol h - a hossza az intervallum, s - standard deviáció értékei számos mérési

Friedman Deaconess képletű (Freedman és Diaconis, 1981)
, ahol h - a hossza az intervallum, (IQ) - a különbség a felső és az alsó kvartilist.

Ezek a képletek meglehetősen egyszerű és megbízható statisztikai elmélet, és tartják előnyös képlet Sturgess.

Azonkívül, hogy szerkesztettünk egy hisztogram segítségével az osztályok száma kapott képletű Sturgess, hisztogramok épülnek a osztályok száma, és Scott Friedman / Deaconess, valamint az osztályok száma, a felhasználó tetszőlegesen állítunk be.

Természetesen a gyakorlati alkalmazása a számológép, nem, de láthatjuk a különbséget az osztályok száma, és a megjelenése a hisztogram.