nyomaték 1
Tegyük szerinti szerv az F erő, a ponton alkalmazzák, A hozzuk forgási tengelye körül OO „(ábra. 1.14).
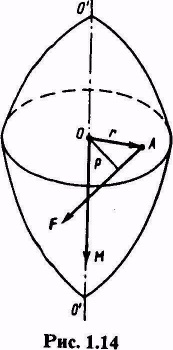
Jelenleg silyest által definiált vektor vektor termék a sugár vektor az erőhatás, és az erő vektor:
(3.1)
Egység pillanatban erő - newtonméter (N • m).
Irány M megtalálható a jobb oldali csavart szabályt.
Impulsachastitsy pillanatban egy vektor termék a sugár vektor részecske annak lendület:
vagy L = a skalár gPsin # 945;
Ez a vektor nagysága és ugyanabban az irányban, mint a vektorok # 969;.
§ 3.2 A tehetetlenségi nyomaték. Steiner-tétel
Az intézkedés tehetetlenségi szervek az előre mozgó tömeget. Tehetetlenség test alatt forgómozgást nem csak attól függ a tömeg, hanem annak eloszlása térben képest a forgástengely. Az intézkedés a tehetetlenség, amikor a forgómozgást egy olyan érték, Vai nevezett tehetetlenségi nyomaték forgástengely körül.
A tehetetlenségi nyomaték az anyag pont tekintetében a forgástengely-ció a termék tömegének a pontokat a tér a távolság a tengelye:
Tehetetlenségi nyomaték tekintetében a forgástengely az úgynevezett összeg-mo Ments tehetetlenségi tömeg pontok, ahonnan a szervezet magában foglalja:
Tehetetlenségi nyomatéka a test függ relatív tengelyen forog, és osztják el a súlyt térfogat.
Most egyszerűen határozza meg a tehetetlenségi nyomatéka szervek, amelyek geometriailag szabályos alakú és egyenletes eloszlását tömeg térfogat.
· A tehetetlenségi nyomaték egy egységes rúd tengely körül közepén áthaladó a tehetetlenség és merőleges a rúd
· A tehetetlenségi nyomaték egy egységes henger tengely körüli perpen-dikulyarnoy annak bázis és áthaladó a tömegközéppont,
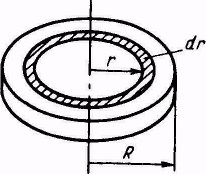
· A tehetetlenségi nyomaték egy vékony falú hengeres, vagy burkolja merőleges tengely körül, hogy a síkjára annak bázis és a középpontján átmenő,
· A tehetetlenségi nyomaték átmérője labda
A képleteket a tehetetlenségi nyomatékok testeket, hogy a forgástengely áthalad a tömegközéppont. Annak megállapításához, a tehetetlenségi nyomatékok tetszőleges tengelye, használja Steiner-tétel: a tehetetlenségi nyomaték egy tetszőleges forgástengely összegével egyenlő a tehetetlenségi nyomaték párhuzamos tengely körül, hogy ez a középpontján áthaladó tömeg, és a termék súlya a távolság négyzetével tengelyek közötti:
[M - test tömege, d - távolság a tömegközéppontja a kiválasztott tengely Vera-scheniya (közötti távolság tengelyek)].
Egység tehetetlenségi - kilogramm méteres négyzetével (kg • m 2).
Így a tehetetlenségi nyomatéka egységes rúd egy olyan tengely körül, amely átmegy annak végén a Steiner-tétel van
§ 3.3 Az egyenlet a rotációs dinamikájának merev test mozgása
Tekintsük először az anyag pont m tömegű, mozgó kerülete mentén r sugarú (ábra. 1.16). Hadd állandó erő F mentén irányul, amelyet a körnek. Szerint a Newton második törvénye, ez az erő a tangenciális gyorsulás, vagy az F = ma # 964; .
Használata az arány egy # 964; = # 946; r. Kapunk F = m # 946; r.
Szorzása egyenlet mindkét oldalát fent leírt r.
Fr = m # 946; R 2 (3,13)
A bal oldalon a expresszió (3.13) az a pillanat erő M = Fr. A jobb oldalon van a termék a szöggyorsulás # 946; a tehetetlenségi nyomatéka az anyag pont: J = m r 2.
A szöggyorsulás a pont a forgatás során egy rögzített tengely a nyomatékkal arányos, és fordítottan arányos a tehetetlenségi nyomaték (alapvető dinamikus egyenlet a forgómozgásának az anyag pont):
M = # 946; Vagy J (3,14)
Ha állandó nyomaték forgási ereje szöggyorsulással állandó érték, és lehet kifejezni különbség a szögsebessége:
Ezután a alapegyenletének dinamikájának forgómozgást felírható
[Az a pillanat, az impulzus (vagy perdület), M # 916; t - impulzus nyomaték (vagy impulzus nyomaték)].
A alapegyenletének dinamikájának forgómozgást felírható
§ 3.4 A törvény megőrzése perdület
Tekintsük a gyakori esetben forgómozgást, ha a teljes pillanatban a külső erők nulla. Amikor a forgási mozgás a test minden egyes részecske mozog egy lineáris sebességgel # 965; = # 969; r, [r, - a kör sugarát, amely leírja a részecske-tömeg m, # 969; - szögsebessége egyenlő az összes pontot a szervezetben].
Impulzusnyomatékhajtómű egy forgó test összegével egyenlő a pillanatok
az egyes részecskék impulzus:
Megváltoztatása perdület egyenlő a nyomaték impulzus:
Ha a teljes idejét ható külső erők a test rendszer tekintetében egy tetszőleges rögzített tengely nulla, azaz M = 0, dl, és a vektor összege pillanatok szervek impulzus rendszer nem változik az idővel.
Az összeg a perdület valamennyi szerv elszigetelt rendszer változatlan marad (a törvény megőrzése perdület):
d (J # 969;) = 0 J # 969; = const (3,20)
A törvény szerint a természetvédelmi impulzusmomentum felírható
ahol J1 és # 969; 1 - a tehetetlenségi nyomaték és a szögsebesség a kezdeti időben, és a J2 és # 969; 2 - t idő.
A megmaradási törvénye impulzusmomentum következik, hogy M = 0, a rotációs rendszer tengelye körül bármilyen változás a távolság a szerveket, hogy a forgástengely kell kísérnie változások a sebesség ezen tengely körül. A távolság növekedésével a fordulatszám párhuzamosan csökken - növekedés. Például egy tornász végző bukfencet, hogy kész a levegőben néhány fordulattal az ugrás közben a labdát a véralvadás. Balerina vagy műkorcsolyázó, köröznek a piruett, széttárja a karját, ha azt akarja, hogy lelassítja a forgatás, és éppen ellenkezőleg, nyomja őket a test, amikor megpróbálja forgatni a lehető leggyorsabban.
§ 3.5 A mozgási energia egy forgó test
Mi határozza meg a kinetikus energia a szilárd test körül forgó rögzített tengely. Osztjuk a test n tömeges pont. Minden pont mozog lineáris sebességgel # 965; i = # 969; ri. akkor a mozgási energia egy pont
A teljes mozgási energia egy forgó merev test összegével egyenlő a mozgási energiáját annak minden lényeges ponton:
(J - tehetetlenségi nyomaték viszonyított forgástengelyével)
Ha a pályái összes pontok rejlik párhuzamos síkokban (mint a henger, lecsúszott a ferde sík, minden egyes pontot mozgatjuk annak síkjában ábrán), ez a sík mozgást. A elvével összhangban az Euler sík mozgás mindig számtalan módon bontjuk transzlációs és rotációs mozgás. Ha a labda leesik, vagy csúszik a ferde sík, akkor mozog csak fokozatosan; ha a labda gurul - és ez még forog.
Ha a szervezet végzi transzlációs és rotációs mozgást egyidejűleg, a teljes mozgási energia
Összehasonlítása alapján a kinetikus energia a képleteket, a második transzlációs és rotációs mozgások is látható, hogy az intézkedés a tehetetlenség, a rotációs-mozgás Tel'nykh tehetetlenségi nyomaték.
§ 3.6 A munka a külső erők forgása során egy merev test
Ha egy merev test forog, annak potenciális energia nem változik, ezért az elemi munkát a külső erők egyenlő a növekmény a kinetikus energia a test:
Tekintettel arra, hogy J # 946; = M, # 969; dr = d # 966;, van
# 916; A = M # 916; # 966; (3,24)
A munka a külső erők a merev test forgása révén egy véges szögben # 966; jelentése
Amikor szilárdtest körüli forgás rögzített tengely munka hatására a külső erők, a pillanat ezeknek az erőknek képest ezen a tengelyen. Ha a nyomaték, ami a tengely nulla, ezek az erők nem termelnek munkát.