Nye fogalmak és meghatározások
Hőcserélő úgy végezzük hőátadást anyagátadási a folyadék vagy gáz mozgása az úgynevezett konvekciós hőátadás. A konvektív hőátadás két komponens lehet megkülönböztetni: a tiszta konvekciós. azaz Csak hőátadás miatt tömeges átvitel és hővezetés. azaz molekuláris hőátadás, amely még mindig végzik a folyadék vagy gáz.
Konvektív hőátadás - a konvektív hőátadás között a folyadék vagy gázáram, és érintkeztetjük egy szilárd felületre. Kiszámításakor felhasznált hő Newton-Richman:
,
ahol tpov - felületi hőmérséklet, amellyel a hőcsere végbemegy, TSR - az előremenő hőmérséklet. A problémát a konvektív hőátadási tényező α a kívánt értéket. Kísérletileg ezt úgy definiálhatjuk, mint a sűrűsége a hőáram a határoló felülete a környezet, osztva a különbsége hőmérsékletek.
Konvekciós lehet szabad (természetes) vagy kényszerített. Természetes konvekció jelentkezik eredményeként egy inhomogén sűrűség eloszlása a közeg térfogatát egy külső gravitációs mezőben. Kényszerített konvekciós történik az intézkedés alapján a külső erők hatnak a határait a térfogatának folyadék vagy gáz, rovására a korábban jelentett kinetikus energia (szivattyú, szél, ventilátor).
2. Fizikai tulajdonságok a közeg (folyadék vagy gáz).
A folyamat a konvektív hőátadás alapvetően függ a fizikai tulajdonságai a mozgó közeg. A már ismert számunkra jellemzőit termikus környezet
(C, λ, ρ. A). fontos szerepet játszott azáltal, hogy a közeg viszkozitása együttható μ. Viszkozitás tulajdonság az összes valós környezetben. Vezessük be a viszkozitás az alábbiak szerint. Azt figyeltük meg, hogy között egybefüggő réteg folyékony különböző sebességgel mozgó, egy erő a belső súrlódás ellentétes a mozgás. Szerint a Newton, ez az erő egységnyi területe arányos a sebesség gradiens a merőleges irányban a menetirány:
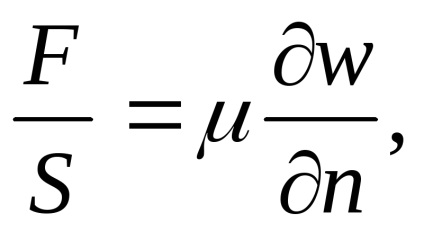
ν = μ / ρ. Könnyen méreteit határozzák meg ezeket a tényezőket:
║μ ║ = kg / (m * c) = H * s / m2 = Pa * s; ║ν ║ = 2 m / s. viszkozitása együtthatók függhet hőmérsékleten.
3. A differenciálegyenletek konvektív hőátadás.
Ha figyelembe vesszük az áramok nyílt rendszerek, a hőátadás folyamat általában úgy izobár. Ezért, a hőmennyiség által hordozott a közeg, rendszerint társítja átadása entalpia. Ha a környezet kiosztani egy sík, ennek eredményeként a konvekciós során dτ át rajta melegíti Q1-2 = dmh1-2 = ρwdτЅh1-2. Ezután a hőáram társított konvekciós, egyenlő lesz ρwh1-2. egy hőáram sűrűsége, kapcsolódik a hővezető egyenlő -λgradt. Vektor formában, a hőfluxus a konvektív hőátadás a következőképpen írható fel:
Annak megállapításához, a hőátadási tényező a hőmérséklet területén és megtalálják rendszer segítségével konvektív hőátadás egyenletek, amely a következő egyenletek:
egyenletek a mozgás a közeg (a Descartes-féle koordináta-rendszer, - a vetített az x, y, z);
hőátadás egyenletet határa a szilárd és folyékony.
3.1. A kontinuitási egyenlet
Ez az egyenlet következik a törvény tömegmegmaradás, amelyek a következőképpen foglalhatók össze:
Sebesség
= Összekötő felhalmozódása - ellátás
súly súly súly
Ahhoz, hogy a matematikai kifejezést az e törvény, szükség van egy derékszögű koordinátarendszerben kiosztani elemi közeg térfogatát formájában egy kocka élei dx, dy, dz és úgy tömegáram keresztül minden arcát. Ha az adatfolyam sebességgel mozog w. hogy az x irányban az egész arc dydz során dτ tömeges közeg áramlik. Keresztül átellenes oldalán az ugyanazon a területen azt jelenti, tömege. A különbség ezek között van a felesleges tömege (akkumuláció) az előnyös a tömeg per térfogat elem scheth - áramlási komponens: Ugyanez a megfontolás kell tölteni dlyay- és Z- komponensei áramlás. Ezután az összeg lesz a sebessége a tömeges felhalmozódása az elemi térfogat dV:
A kifejezést a zárójelek jelentése a divergencia (ρw). Ezért végül a kontinuitási egyenlet (vagy diszkontinuitás) van írva, mint:
Abban az esetben, állandó sűrűségű, (2) egyenlet alakítjuk
(3) egyenlet - a folytonosság egyenlet összenyomhatatlan folyadékot.